Обзор существующих научных работ по системе планово-предупредительного ремона, страница 6

L, моточасов	РВ(L)	Pср(L)	PH(L)
2000	0,9972	0,9962	0,9949
2500	0,9897	0,9863	0,9817
3000	0,9705	0,9611	0,9481
3500	0,9295	0,9076	0,8779
4000	0,8533	0,8104	0,7539
4500	0,7305	0,6597	0,5717
5000	0,5608	0,4647	0,3571
5500	0,366	0,2641	0,1671
6000	0,1893	0,1102	0,0516
6500	0,0708	0,03	0,009
7000	0,0171	0,0046	0,0007
7500	0,0023	0,0003	0
8000	0,0001	0	0
8000	0,0001	0	0
8500	0	0	0

На основании расчетных данных таблицы 3.2построим график вероятности безотказной работы фрсунок двигателя Deutz автобуса МАЗ – 103. (рисунок 3).

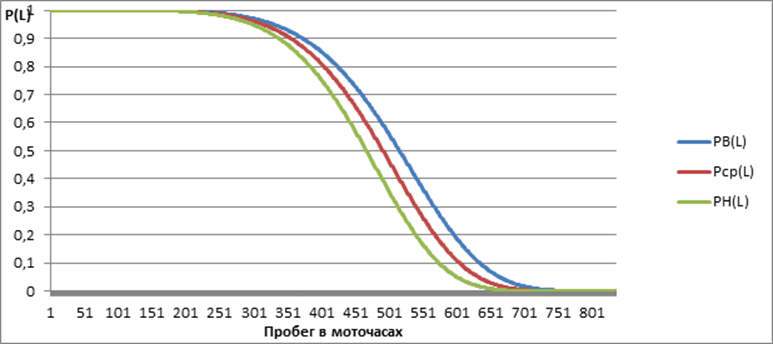
Рисунок – 3 Вероятность безотказной работы системы форсунок

Оценка гамма-процентной нарабтки до отказа.

Согласно ГОСТ 27.002-83: гамма-процентная наработка до отказа -  - это наработка, в течении которой отказ элемента АТС не возникает с вероятностью .

Для невосстанавливаемых элементов является одновременно показателем долговечности — гамма-процентным ресурсом (наработкой в течении которой элемент АТС не достигнет предельного состояния с заданной вероятностью).

Для закона Вейбула-Гнеденко точечная оценка гамма-поцентной наработки до отказа, тыс.км:

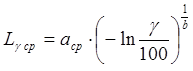                                               (3.18)

где  - гамма-процентная наработка до отказа (точечная оценка), тыс.км.;

- вероятность того, что заданный элемент АТС не достигнет предельного состояния, %.

Интервальную оценку  определим при подстановке в формулу (3.18) вместо  значения и .

По рисунку 3 можно определить гамма-процентную наработку до первого отказа.

Для этого параллльно оси абсцисс проведем прямую линию через точку .

Пусть . Тогда .

Абсциссы точек пересечения этой прямой с кривыми ,  и  дают точечную и интервальную оценки гамма-процентной наработки до первого отказа.

Для более точной оценки используме формулу (3.18).

Получим следующие оценки:

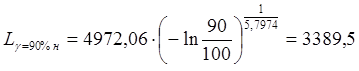
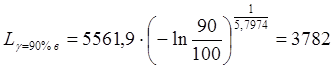
Оценка интенсивности отказа.

Интенсивность отказов— условная плотность вероятности возникновения отказа невосстанавливаемого элемента АТС, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник.

Для закона Вейбула-Гнеденко точечная оценка интенсивности отказов:

                                          (3.19)

где - интенсивность отказов (точечная оценка), .

Интервальную оценку  определим при подстановке в формулу (3.19) вместо  значения и .

Расчет произведем табличным способом. Результаты расчета представлены в таблице 3.3для точечной оценки, нижнего доверительного интервала и верхнего доверительного интервала соответственно

Таблица 3.3 – Точечная оценка интенсивности отказов