Обзор существующих научных работ по системе планово-предупредительного ремона, страница 5

                                      (3.10)

Разделим на S интервалов размах вариационного ряда, т.е. разность между наибольшим и наименьшим числами.

Границы интервала найдем по формуле:

                                         (3.11)

где - номера интервалов;

L_max – максимальное значение вариационного ряда, моточасов;

L_min – минимальное значение вариационного ряда, моточасов;

Расчет размаха интервала эпирических частот произведем табличным способом. Результаты представлены в таблице 3.1.

Таблица 3.1 – Расчет эмпирических частот

j	Lj	Lj+1	nj	nj²	∆F(Lj)		nj²/
1	0	573,5	6	36	0,106	4,25	8,47
2	573,5	1147	5	25	0,132	5,27	4,75
3	1147	1720,5	6	36	0,204	8,19	4,39
4	1720,5	2294	11	121	0,240	9,63	12,57
5	2294	2867,5	6	36	0,195	7,8	4,61
6	2867,5	∞	6	36	0,095	3,81	9,43

Определим эмпирические частоты, т.е.— количество членов вариационного ряда, попавших в j-ый интервал (см. таблицу 3.1).

2.  Исходя из нулевой гипотезы, рассчитаем теоретические частоты по формуле:

                                            (3.12)

где - вероятность отказа для  члена;

 - вероятность отказа для  члена.

Функцию распределения отказов, входящую в формулу (3.12), определим по формуле.

Для закона Вейбулла-Гнеденко:

                                           (3.13)

Для нормального закона распределения:

                                       (3.14)

Расчет  произведем табличным способом (см. таблицу 3.1).

3. Определить расчетное значение критерия Пирсона

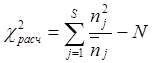                                           (3.15)

Для закона Вейбулла-Гнеденко:

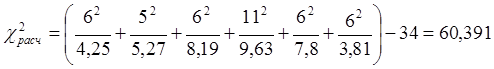
Для нормального закона:

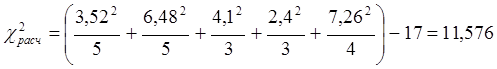
Определим число степеней свободы:

                                          (3.16)

где r- количество параметров предполагаемого распределения.

Для закона Вейбулла-Гнеденко:

Значит,  по /1/:

Условие:

 (верно)

Гипотеза выполняется, так как 5,7974<60,391.

Для нормального закона:

Значит,  по /1/:

Условие:

 (не верно)

Гипотеза не выполняется, так как 11,576>5,992.

Таким образом, принимаем закон распределения Вейбулла-Гнеденко для генеральной совукопности.

Оценка вероятности безотказной работы:

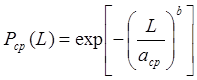,                                   (3.17)

где - вероятность безотказной работы (точечная оценка).

Интервальную оценку  определим при подстановке в формулу (3.17) вместо  значения и .

Расчет произведем табличным способом. Результаты расчета представлены в таблице 3.2 для точечной оценки, нижнего доверительного интервала и верхнего доверительного интервала соответственно

Таблица 3.2 – Точечная оценка вероятности безотказной работы, нижний и верхний доверительные интервалыфорсунки двигателя Deutz автобуса МАЗ – 103

L, моточасов	РВ(L)	Pср(L)	PH(L)
0	1	1	1
500	1	1	1
1000	0,9999	0,9999	0,9999
1500	0,9995	0,9993	0,999

Окончание таблицы 3.2