Министерство образования и науки РФ
ГОУВПО «Комсомольский-на-Амуре государственный технический университет»
Кафедра МОП ЭВМ
Отчет №4
По дисциплине «Ознакомительная практика»
Выполнил: Сюй Н.А.
Группа: 4ВС-1
Проверил: Могильников Е.В.
Комсомольск-на-Амуре
2005
Постановка задачи:
Функция ![]() задана своим аналитическим выражением на
интервале. Приближенно вычислить определенный интеграл от заданной функции на
этом интервале методом трапеций с заданным разбиением
задана своим аналитическим выражением на
интервале. Приближенно вычислить определенный интеграл от заданной функции на
этом интервале методом трапеций с заданным разбиением ![]() .
Привести оценку остаточного члена и оценить погрешность вычислений по правилу
Рунге практической оценки погрешности. Привести точное решение и сравнить с полученным.
.
Привести оценку остаточного члена и оценить погрешность вычислений по правилу
Рунге практической оценки погрешности. Привести точное решение и сравнить с полученным.
Заданная функция:
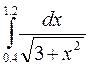
Алгоритм решения:
1. Перед программами располагаются общие для них данные: границы интервала, количество разбиений и шаг изменения переменной. Также указана формула трапеций с помощью, которой будет производить вычисление интеграла:
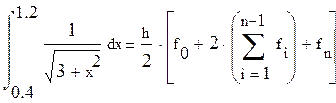
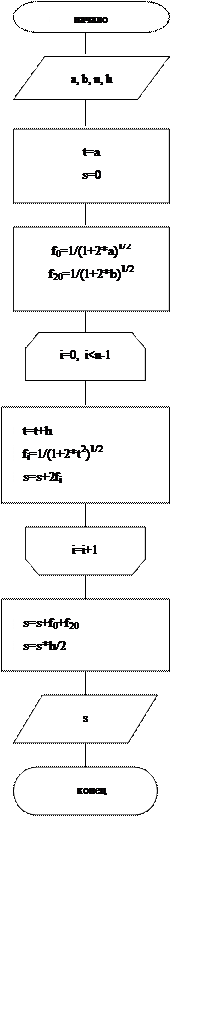
2. Программа для вычисления определенного интеграла с помощью формулы трапеций. В цикле программы вычисляются значения функции на интервале [1.2, 2.4] с шагом 0,006. После цикла к накопленной в нем сумме прибавляется значения функции в граничных точках отрезка и все умножается на половину шага.
3. Программа
для вычисления остаточного члена по формуле: 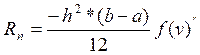 , где h-это шаг, f(v)-
максимальное значение второй производной функции на интервале [0.4, 1.2]. v-точка в которой вторая производная принимает максимальное
значение. Для выбора точки v: Найдем корни третьей
производной (-2.121, 0, 2.121) т.к. она принимает положительное значение на
заданном интервале, следовательно, вторая производная на этом интервале возрастающая.
Найдём её значение по модулю в точках 0.4 и 1.2 (0.151,0.002889). Сравнив два
значения, выберем ту точку, в которой значение наибольшее. В программе сначала
вычисляется значение второй производной, затем сам остаточный член и
осуществляется его вывод.
, где h-это шаг, f(v)-
максимальное значение второй производной функции на интервале [0.4, 1.2]. v-точка в которой вторая производная принимает максимальное
значение. Для выбора точки v: Найдем корни третьей
производной (-2.121, 0, 2.121) т.к. она принимает положительное значение на
заданном интервале, следовательно, вторая производная на этом интервале возрастающая.
Найдём её значение по модулю в точках 0.4 и 1.2 (0.151,0.002889). Сравнив два
значения, выберем ту точку, в которой значение наибольшее. В программе сначала
вычисляется значение второй производной, затем сам остаточный член и
осуществляется его вывод.
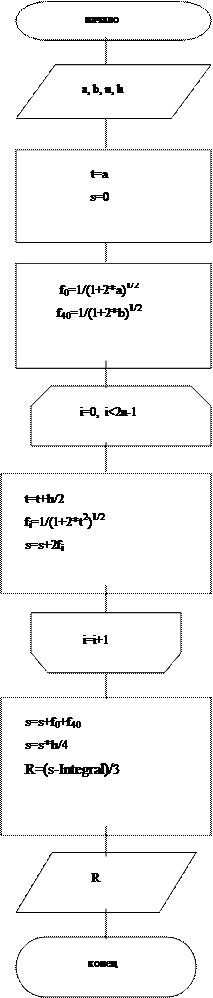
4. Программа для определения практической погрешности по правилу Рунге. В ней происходит вычисление значения интеграла на данном промежутке, но с шагом h/2. После вычисления этого значения вычисляется погрешность по формуле:
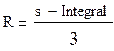 где s – значение интеграла вычисленного с половинным шагом, Integral – значение интеграла, вычисленное нормальным шагом.
где s – значение интеграла вычисленного с половинным шагом, Integral – значение интеграла, вычисленное нормальным шагом.
5. Сравнение точного значения интеграла со значением полученным программой.
Блок-схема программы для вычисления интеграла с помощью формулы трапеций:
 |
Блок-схема программы для вычисления остаточного члена:
 |
Блок-схема программы для определения практической погрешности по правилу Рунге:
 |
Листинг программы:
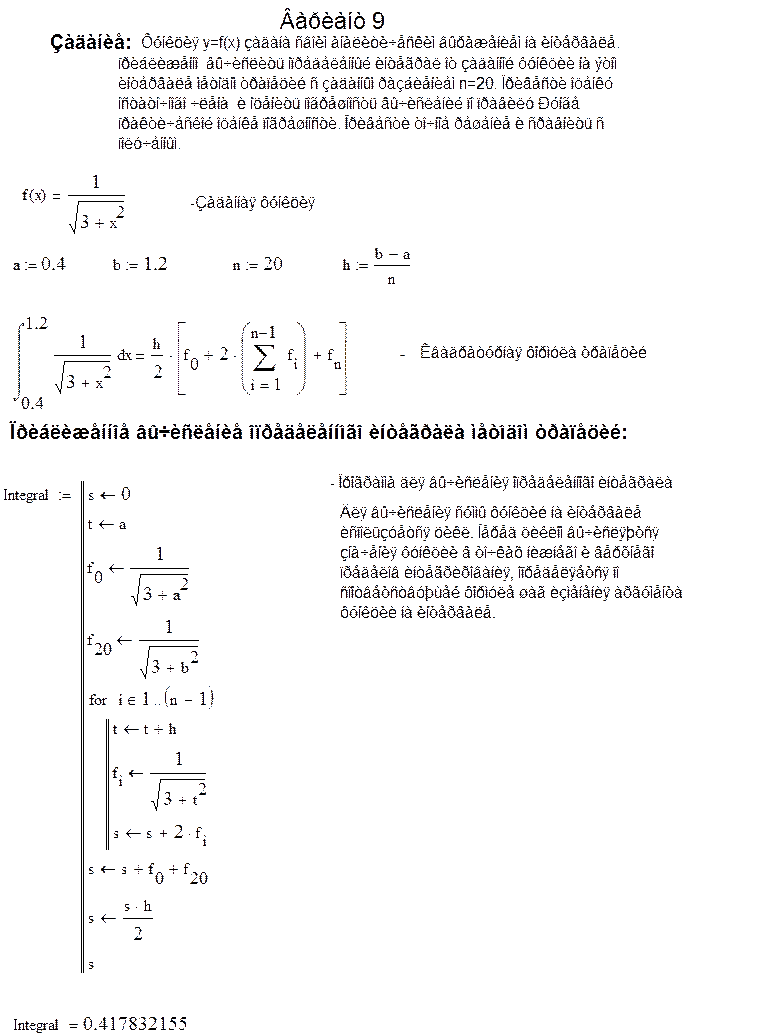
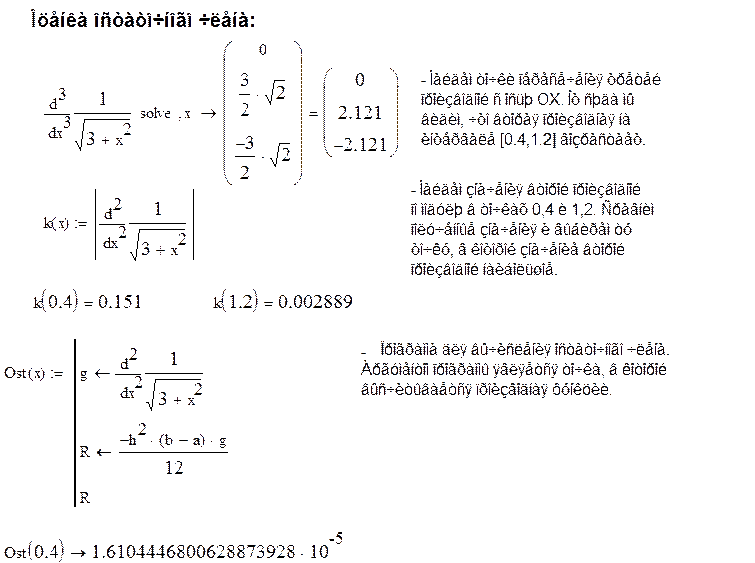
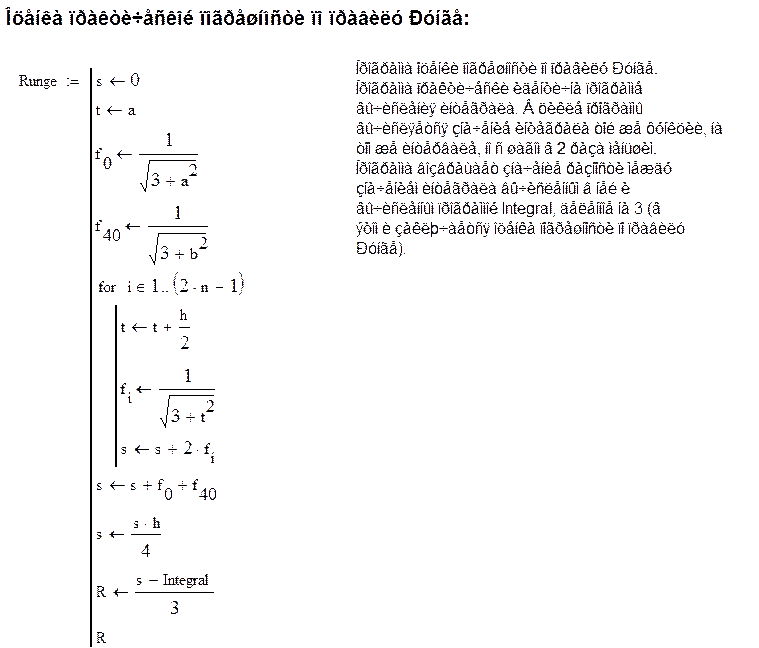
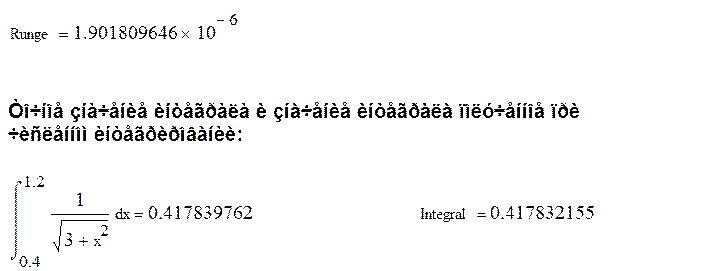
Список использованной литературы:
Боглаев Ю.П. Вычислительная математика и программирование. Москва «Высшая школа», 1990.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.