Вычисление определителя и обратной матрицы для заданной с помощью LU разложения

Министерство образования и науки РФ

ГОУВПО «Комсомольский-на-Амуре государственный технический университет»

Кафедра МОП ЭВМ

Отчет №5

По дисциплине «Ознакомительная практика»

Выполнил: Сюй Н.А.

Группа: 4ВС-1

Проверил: Могильников Е.В.

Комсомольск-на-Амуре

2005

Вариант 9

Постановка задачи.

Вычислить определитель и обратную матрицу для заданной с помощью LU разложения.

Заданная система уравнений:

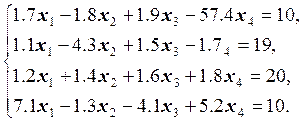
Алгоритм решения.

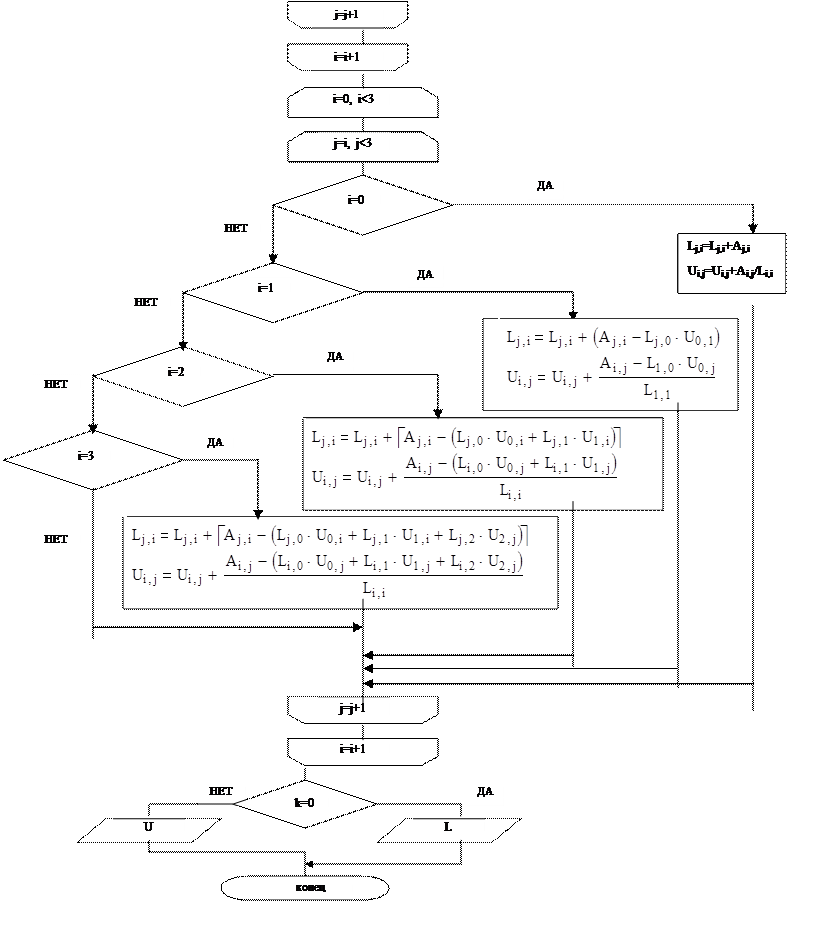
1.  Вычисление матриц L и U. В программе, в которой вычисляются матрицы, сначала происходит обнуления всех элементов матрицы, а затем к соответствующим элементам прибавляются значения элементов, вычисленных по формулам:

                            

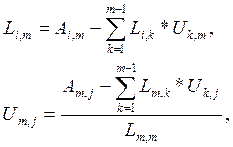
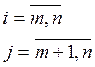
Заполнение матриц происходит по столбцам (для матрицы L) и строкам (для матрицы U), т.к. для каждого столбца (матрица L) и для каждой строки (матрица U) накапливаются различные суммы.

Программа содержит аргумент k. Он может принимать значения 0 или 1. Если k=0, то результатом программы является матрица L, в противном случае – матрица U.

2.  Для того, чтобы вычислить определитель матрицы А, мы должны перемножить определители матриц L и U. Матрицы являются треугольными, т.е. определитель равен произведению элементов главной диагонали. Т.к. в  матрице U элементы главной диагонали равны единицам, то  в программе поиска определителя матрицы А рассчитывается произведение элементов главной диагонали матрицы L.

3.  Вычисление матриц, обратных матрицам L и U. В начале программы происходит обнуление элементов обоих матриц. Программа содержит переключатель k, если k равен нулю, то вычисляется и выводится матрица L^-1, в противном случае U^-1. При вычислении каждой из матриц происходит проверка, находится ли элемент на главной диагонали. Элементы главной диагонали вычисляются по формулам:

 

соответственно.    

Остальные элементы вычисляются по следующим формулам:

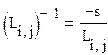     , где     

    , где      

4.  Обратная матрица   вычисляется по формуле: .   

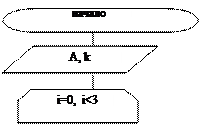
Блок-схема программы для вычисления матриц L и U:

 

                              

 

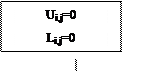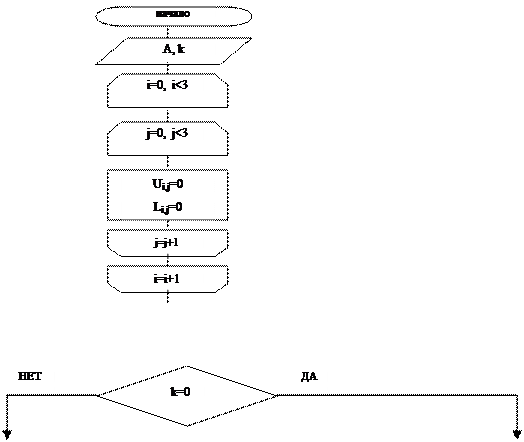
Блок-схема программы для вычисления матриц, обратных матрицам L и U:

 

 

 

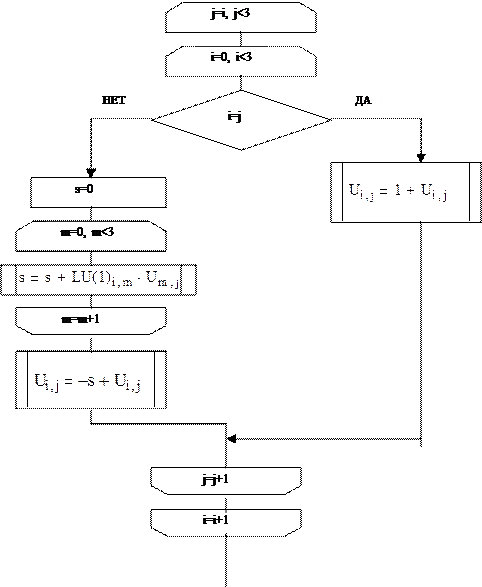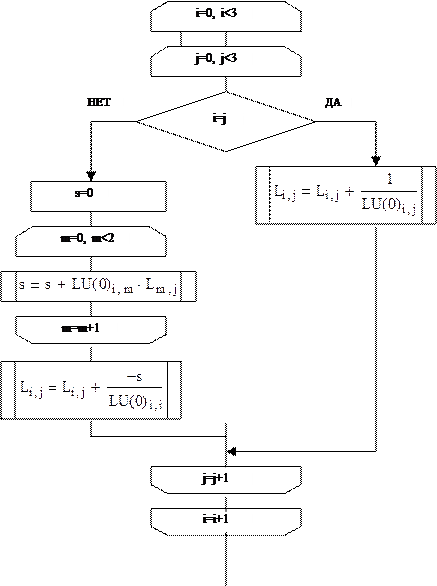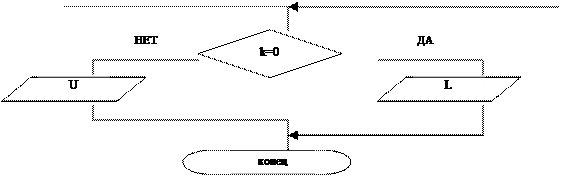 Листинг программы:

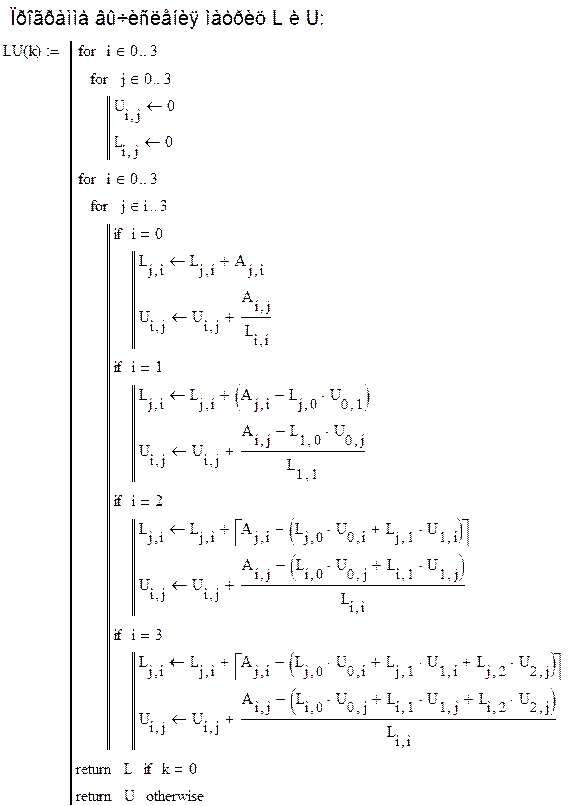
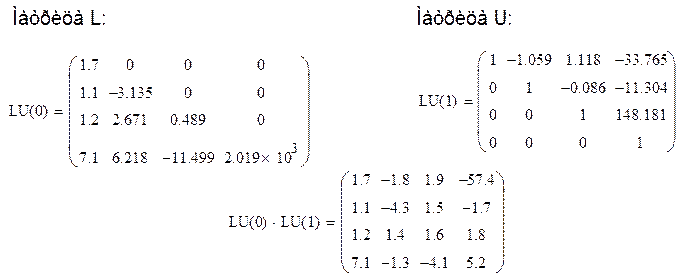
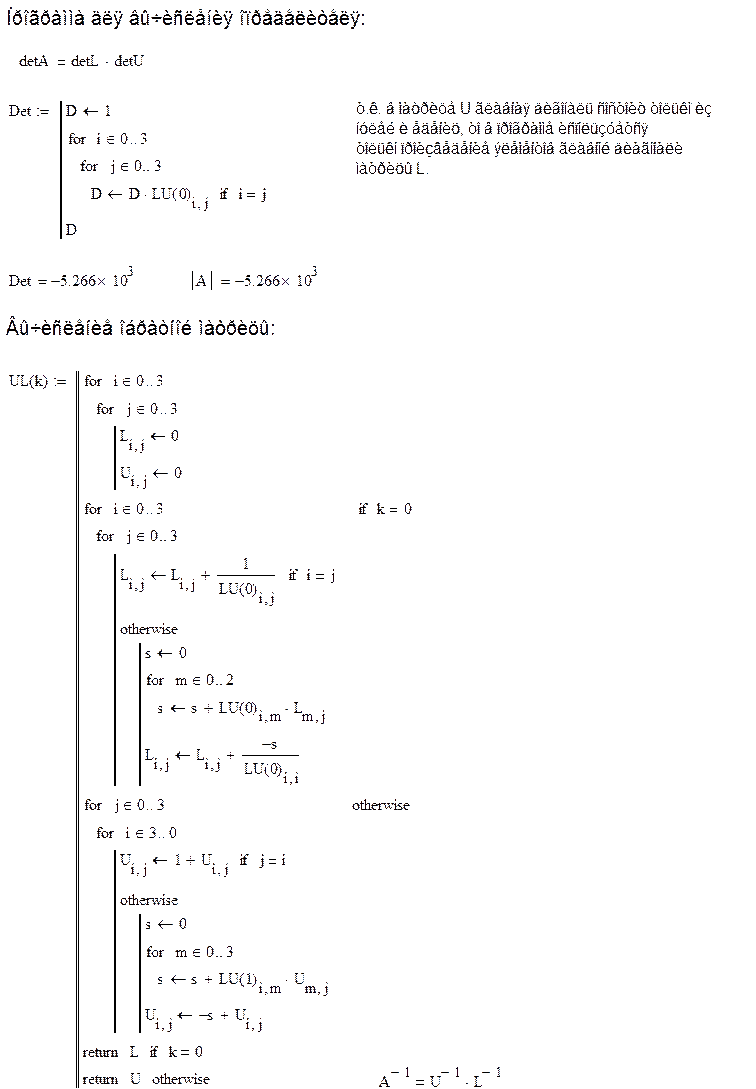
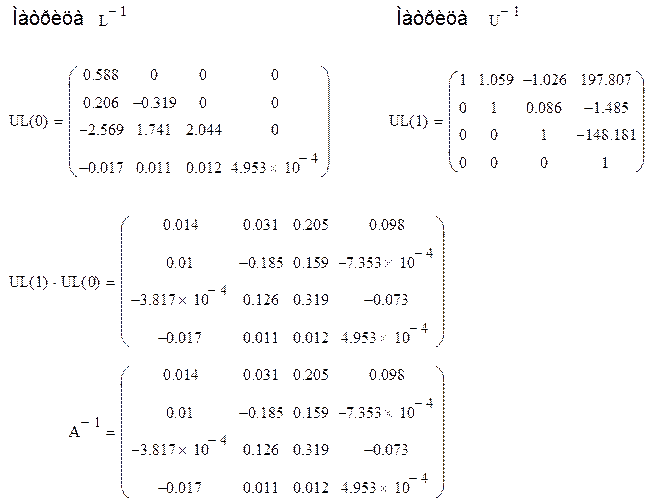
Список использованной литературы:

Боглаев Ю.П. Вычислительная математика и программирование: Учебное пособие для студентов втузов. – М.: Высшая школа, 1990. – 544 с.