












ВАРИАНТ №21
Задание:
Определить класс, объектами которого являются многоугольники указанного типа. Написать тест на принадлежность точки многоугольнику с помощью указанного алгоритма. Определить операцию вывода многоугольника в окно с помощью дружественной функции. Определить операцию преобразования многоугольника с помощью составной функции.
Меню включает опции: Ввод точек, Выполнение действия, Выход, Помощь.
Точки вводятся с помощью мыши или генератора случайных чисел.
Тест на принадлежность точки многоугольнику в нечетных вариантах выполняются методом горизонтального луча
Класс:
K4. Выпуклый многоугольник, производный от K1. Конструктор строит выпуклую оболочку методом Дейкстры..
Преобразование:
P2. Вращение на угол a вокруг точки (x,y).
Теоретические сведения:
Класс выпуклого многоугольника определим как производный от класса Spolygon. Конструктор будет строить выпуклый многоугольник как выпуклую оболочку с помощью алгоритма Дейкстры, основанному на приведенной ниже идее.
Пусть М – выпуклый многоугольник, р – произвольная внешняя точка. Сторона многоугольника называется видимой из точки р, если существует такая точка q, принадлежащая этой стороне, что отрезок, соединяющий ее с точкой р, не имеет других общих точек со стороной, кроме точки q. На рис. 5.4 видимыми будут стороны S0S1, S1S2 и S5S0. В частности, для стороны S5S0 такой точкой q будет S0.
Если задан выпуклый многоугольник и точка р, то удаляя видимые стороны и соединяя точку р с двумя крайними точками оставшихся сторон, получаем выпуклый многоугольник, который будет выпуклой оболочкой точек Si и р.
Конструктор строит выпуклую оболочку, последовательно добавляя по одной точке к предшествующим выпуклым многоугольникам.

Тест принадлежности методом луча. Рассмотрим алгоритм, основанный на определении внутренней точки, данном в стандарте GKS. Пусть луч пересекается с многоугольником в точках, являющихся вершинами многоугольника (рис. 6.1).
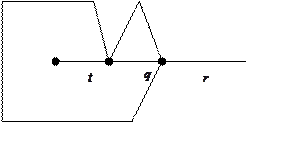 |
Рис. 6.1. Пример расположения точки и многоугольника
В этом примере луч пересекается с границей многоугольника в четном числе точек, хотя точка является внутренней. Если же подсчитывать число пересечений луча со сторонами многоугольника, то точка q и точка r будут учитываться дважды, и вновь получаем четное число пересечений со сторонами многоугольника.
Анализ этого примера приводит к выводу, что точку q следует учитывать два раза или не учитывать совсем, а точку r — один раз. Следовательно, при определении, пересекаются ли горизонтальный луч и отрезок, мы не должны учитывать точки отрезка, имеющие максимальную ординату.
В примере (рис. 6.1) получаем, что число точек пересечения со сторонами равно 1 + 1 + 1 + 0.
Алгоритм проверки на принадлежность точки t многоугольнику p0, p1,…,pn-1 будет состоять из следующих действий:
1. Установить четность parity = 0.
2. Организовать цикл по i = 0, 1, 2,…,n-1, в теле которого, в случае, когда пересечение луча, проведенного вправо от точки t, с отрезком pip(i+1)%n не пусто, применяется операция изменения четности parity = 1 – parity.
3. После окончания работы цикла, если parity = 1, то точка расположена внутри, а в случае parity = 0 — снаружи многоугольника.
При программной реализации проверка на пересечение луча и отрезка будет осуществляться в подпрограмме (функции), возвращающей 1, если пересечение не пусто, и 0 — в противном случае. Если общей точкой луча и отрезка является точка отрезка с максимальной ординатой, то возвращается 0. В частности, пересечение луча с горизонтальным отрезком всегда считается пустым. Луч, исходящий из точки (x, y), будет пересекаться с отрезком, соединяющим точки (x1, y1) и (x2, y2), если min (y1, y2) ≤ y < max (y1, y2) и, более того, точка пересечения горизонтальной прямой с отрезком находится справа от точки (x, y).
Текст программы:
Текстфайла poly.h
#define PI 3.14159 //определяем число пи
//--------------------------------------------------------------------------struct Pnt // класс точки
{
double x, y; // координаты точки
int code(Pnt q); // код четверти, в которой лежит точка q
double operator*(Pnt q); // векторное произведение
Pnt operator-(Pnt q); // разность векторов
};
//--------------------------------------------------------------------------int Pnt::code(Pnt q) // код четверти, в которой лежит точка q
{
// начало координат находится в точке (x, y)
if(q.x - x >= 0 && q.y - y >= 0) return 0;
if(q.x - x < 0 && q.y - y >= 0) return 1;
if(q.x - x >= 0 && q.y - y < 0) return 3;
if(q.x - x < 0 && q.y - y < 0) return 2;
}
//--------------------------------------------------------------------------double Pnt::operator*(Pnt q)
{
return x * q.y - y * q.x; // векторное произведение
}
Pnt Pnt::operator-(Pnt q) // разность векторов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.