Дистрибутивная ограниченная решетка, в которой для каждого элемента существует дополнение, называется булевой алгеброй.
Свойства булевой алгебры:
1. а ![]() а = а, a
а = а, a
![]() a = a
a = a
по определению решетки;
2. a ![]() b = b
b = b ![]() a, a
a, a![]() b = b
b = b![]() a
a
по определению решетки;
3. а ![]() (b
(b![]() с) = (а
с) = (а ![]() b)
b) ![]() с, a
с, a![]() (b
(b ![]() c) = (a
c) = (a ![]() b)
b) ![]() c
c
по определению решетки;
4. (а ![]() b)
b) ![]() а = а, (a
а = а, (a![]() b)
b) ![]() a = a
a = a
по определению решетки;
5. а ![]() (b
(b ![]() с) = (а
с) = (а ![]() Ь)
Ь) ![]() (а
(а ![]() с), a
с), a ![]() (b
(b ![]() с) = (а
с) = (а ![]() b)
b) ![]() (а
(а ![]() с)
с)
по свойству дистрибутивности;
6. а ![]() 1= 1, а
1= 1, а
![]() 0 = 0
0 = 0
по свойству ограниченности;
7. а ![]() 0 = а, а
0 = а, а
![]() 1 = 0
1 = 0
по следствию из теоремы ограниченности;
8. а" = а
по теореме о свойствах дополнения;
9. (а ![]() b)' = а'
b)' = а' ![]() b' (a
b' (a
![]() b)' = а'
b)' = а' ![]() b'
b'
по теореме о свойствах дополнения;
10. а ![]() а' = 1, a
а' = 1, a
![]() а' = 0
а' = 0
так как дополнение существует.
Пример
1. <2M;
![]() ,
, ![]() ,- > - булева алгебра, 1 = U, 0 = Ǿ,
,- > - булева алгебра, 1 = U, 0 = Ǿ, ![]() =
= ![]() .
.
2. <Е2;
&, V, ¬> — булева алгебра, 1 = 1,0=1, ![]() =
=![]() .
.
3. Пусть π(р)
: = {q | q ![]() N—
простое & q
N—
простое & q![]() р} — множество простых чисел,
не превосходящих р.
р} — множество простых чисел,
не превосходящих р.
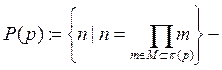
множество произведений различных чисел из π (р).
Тогда <Р; Н.О.Д., Н.О.К., ДОП> — булева алгебра, где Н.О.Д. - наибольший общий делитель, Н.О.К. — наименьшее общее кратное,
ДОП(n): = 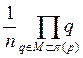 .
.
1:= ![]() , 0: = 1, m
, 0: = 1, m ![]() n: = n делится на m.
n: = n делится на m.
2.7. Матроиды
Матроиды, рассматриваемые в этом разделе, вообще говоря, не являются алгебраическими структурами в том смысле, который был придан этому понятию в первом разделе данной главы. Однако, во-первых, матроиды имеют много общего с рассмотренными алгебраическими структурами (в частности, с линейно независимыми множествами в векторных пространствах) и изучаются сходными методами, а во-вторых, они являются теоретической основой для изучения и анализа «жадных» алгоритмов. Ясное понимание природы и области применимости жадных алгоритмов совершенно необходимо всякому программисту.
2.7.1. Определения
Матроидом М = <Е, e> называется конечное множество Е, |Е| = n и семейство его
подмножеств e![]() 2Е, такое что
выполняются следующие три аксиомы:
2Е, такое что
выполняются следующие три аксиомы:
М1: Ǿ ![]() e;
e;
М2: А![]() e&В
e&В![]() A
A![]() В
В![]() e;
e;
М3: А, В![]() e & |В| = |А| +
1
e & |В| = |А| +
1 ![]()
![]() e
e![]() В\
А А
В\
А А![]() {е}
{е}![]() e.
e.
Элементы множества e называются независимыми, а остальные подмножества Е (2Е \ e) — зависимыми множествами.
ЗАМЕЧАНИЕ———————————————––––––––––––––––––––————–––––––––––––––––––––––
Аксиома М1 исключает из рассмотрения вырожденный случай e = Ǿ.
————————————————————————––––––––––––––––––––————–––––––––––––––––––––––
Пример
Семейство линейно независимых множеств векторов любого векторного пространства является матроидом. Действительно, по определению можно считать,
что пустое множество линейно независимо. Всякое подмножество линейно независимого множества векторов линейно независимо. Пусть A:={а1...,аm} и В: ={b1,..., bm+1} — линейно независимые множества. Если бы все векторы из множества В выражались в виде линейной комбинации векторов из множества А, то множество В было бы линейно зависимым. Стало быть, среди векторов множества В есть по крайней мере один вектор b, который не входит в множество A и не выражается в виде линейной комбинации векторов из множества А. Добавление вектора b к множеству А образует линейно независимое множество.
ЗАМЕЧАНИЕ———————————————––––––––––––––––––––————–––––––––––––––––––––––
Само понятие матроида возникло в результате исследований линейной независимости в векторных пространствах.
————————————————————————––––––––––––––––––––————–––––––––––––––––––––––
2.7.2. Максимальные независимые подмножества
Пусть X![]() Е — произвольное множество.
Максимальным независимым подмножеством множества X называется
множество У, такое что
Е — произвольное множество.
Максимальным независимым подмножеством множества X называется
множество У, такое что
У![]() Х & У
Х & У ![]() Е &
Е &![]() Z
Z ![]() Е Z
Е Z![]() X =Z
X =Z ![]() У.
У.
Множество
максимальных независимых подмножеств множества X обозначим ![]() . Рассмотрим следующее утверждение:
. Рассмотрим следующее утверждение:
М4: ![]() Х (У
Х (У![]()
![]() & Z
& Z ![]()
![]()
![]() |У|=|Z|), то есть
максимальные независимые подмножества данного множества равномощны.
|У|=|Z|), то есть
максимальные независимые подмножества данного множества равномощны.
ТЕОРЕМА Пусть М = <Е, e> и выполнены аксиомы M1 и М2. Тогда аксиома M3 и утверждение М4 эквивалентны, то есть
(A,B![]() E &|B|=|A|+1
E &|B|=|A|+1![]()
![]() e
e![]() B\A A
B\A A![]() {e}E)
{e}E)
тогда и только тогда, когда
![]() X (У, Z
X (У, Z ![]()
![]()
![]() |У|=|Z|)
|У|=|Z|)
Доказательство
Необходимость. Пусть выполнены
утверждения М1, М2, М3 (то есть М
— матроид). Покажем от противного, что выполняется и М4.
Пусть У,Z![]()
![]() , |У|
, |У|
![]() |Z| и для
определенности |У| > |Z|. Возьмем У'
|Z| и для
определенности |У| > |Z|. Возьмем У' ![]() У, так что |У'| = |Z| + 1. Тогда по
свойству М3 имеем:
У, так что |У'| = |Z| + 1. Тогда по
свойству М3 имеем: ![]() е
е![]() У'\ Z W:=Z
У'\ Z W:=Z![]() {е}
{е}![]() e. Таким образом,
имеем W
e. Таким образом,
имеем W![]() e, Z
e, Z![]() W, W
W, W ![]() X, что противоречит
предположению Z
X, что противоречит
предположению Z![]()
![]() .
.
Достаточность. Пусть выполнены
утверждения М1, М2, М4. Покажем от
противного, что выполняется и М3. Возьмем A,В![]() e, так что |В|=|А|+1.
Допустим, что ¬
e, так что |В|=|А|+1.
Допустим, что ¬![]() е
е![]() В\А А
В\А А![]() {е}
{е}![]() e, то есть
e, то есть ![]() е
е![]() В\А А
В\А А![]() {е}
{е}![]() e. Рассмотрим С:=А
e. Рассмотрим С:=А![]() В.
Имеем А
В.
Имеем А![]()
![]() . Но В
. Но В![]() e, поэтому
e, поэтому ![]() В' В
В' В![]() В'&В'
В'&В'
![]() e&В'
e&В' ![]()
![]() . По условию М4
имеем |В'| = |А|. Но |А|=|В'|
. По условию М4
имеем |В'| = |А|. Но |А|=|В'| ![]() |В|=|А|+1 - противоречие.
|В|=|А|+1 - противоречие.
ЗАМЕЧАНИЕ———————————————––––––––––––––––––––————–––––––––––––––––––––––
Таким образом, M1, М2, М4 — эквивалентная система аксиом матроида.
————————————————————————––––––––––––––––––––————–––––––––––––––––––––––
2.7.3. Базисы
Максимальные независимые подмножества множества Е называются базами, или базисами, матроида М = <Е, e>. Всякий матроид имеет базисы, что видно из следующего алгоритма.
Алгоритм 2.1. Алгоритм построения базиса матроида
Вход: Матроид М = <Е, e>.
Выход:
Множество В![]() Е элементов, образующих базис.
Е элементов, образующих базис.
В : = 0 { вначале базис пуст }
for е![]() Е do
Е do
if В![]() {е}
{е}![]() E then
E then
В : = В ![]() {е} {
расширяем базис допустимым образом }
{е} {
расширяем базис допустимым образом }
end if
end for
Обоснование
Алгоритм вычисляет базу матроида М.
Действительно,
пусть В0 = Ǿ, В1,…,Вk = В — последовательность
значений переменной В в процессе работы алгоритма. По построению ![]() i Вi
i Вi ![]() Е. Пусть В
Е. Пусть В ![]() , то есть В не является максимальным. Тогда
, то есть В не является максимальным. Тогда ![]() В' В В' & В'
В' В В' & В' ![]() В & В' Е. Возьмем В"
В & В' Е. Возьмем В"![]() В', так что |В"| = |В| +
1, В
В', так что |В"| = |В| +
1, В ![]() В" и В"
В" и В" ![]() Е. Рассмотрим е В' \ В.
Элемент е не попал в множество В, но алгоритм про сматривает все элементы,
значит, элемент е был отвергнут на некотором шаге i, то есть (Вi-1
Е. Рассмотрим е В' \ В.
Элемент е не попал в множество В, но алгоритм про сматривает все элементы,
значит, элемент е был отвергнут на некотором шаге i, то есть (Вi-1 ![]() {е})
{е}) ![]() E. Но е
E. Но е ![]() В" & Вi-1
В" & Вi-1![]() В"
В" ![]() (Вi-1
(Вi-1 ![]() {е}) е Е. По аксиоме М2 имеем: (Вi-1
{е}) е Е. По аксиоме М2 имеем: (Вi-1
![]() {е})
{е}) ![]() Е — противоречие.
Е — противоречие.
СЛЕДСТВИЕ Все базы матроида равномощны.
2.7.4. Ранг
Мощность максимального независимого подмножества данного множества X называется рангом множества:
![]()
ЗАМЕЧАНИЕ———————————————––––––––––––––––––––————–––––––––––––––––––––––
Это определение корректно, потому что все максимальные независимые подмножества данного множества равномощны.
————————————————————————––––––––––––––––––––————–––––––––––––––––––––––
ЛЕММА X![]() E & Y
E & Y![]()
![]()
![]() X = Y
X = Y
Доказательство
X![]() X & X
X & X![]() E & Y
E & Y![]()
![]()
![]() X
X![]() Y
Y![]() X
X![]() X = Y
X = Y
ТЕОРЕМА:X![]() E
E![]() r (X) = |X|
r (X) = |X|
Доказательство
X![]() E
E ![]() (X
(X![]() E & Y
E & Y![]()
![]()
![]() X = Y)
X = Y) ![]() (r (x) = |X|)
(r (x) = |X|)
ТЕОРЕМА: ![]() A, B
A, B ![]() E
E![]() e1, e2
e1, e2 ![]() E
E
R1 : 0![]() r(A)
r(A) ![]() |A|
|A|
R2
: А![]() В
В![]() r(A)
r(A)![]() r(B)
r(B)
R3
: r(A![]() B) +
r(A
B) +
r(A![]() B)
B) ![]() r(A)+ r(B)
r(A)+ r(B)
R4
: r(A)![]() r(A
r(A![]() {e})r(A)+1
{e})r(A)+1
R5
: r(A![]() {e1})
= r(A
{e1})
= r(A![]() {e2})=
r(A)
{e2})=
r(A) ![]() r(A
r(A![]() {e1,e2})
= r(A)
{e1,e2})
= r(A)
Доказательство
R1 : очевидно;
R2 : очевидно;
R3 :
Пусть {е1,…,еi}![]()
![]() . Тогда {е1,…,еi,
d1,…,di }
. Тогда {е1,…,еi,
d1,…,di }![]()
![]() и
затем {е1,…,еi, d1,…,dj, c1,…,ck,}
и
затем {е1,…,еi, d1,…,dj, c1,…,ck,}![]()
![]() . Имеем i = r (A
. Имеем i = r (A ![]() B), Bi+j = r(A), i +
k
B), Bi+j = r(A), i +
k ![]() i + j + k = r(A
i + j + k = r(A ![]() В)
В) ![]() r(A
r(A ![]() B) + r(A
B) + r(A ![]() B) = (i + j +k) + i = (i + j) + (i + k)
B) = (i + j +k) + i = (i + j) + (i + k) ![]() r(А) + r(В);
r(А) + r(В);
R4: очевидно;
R5 : r(A)![]() r(А
r(А![]() {е1, е2}) = r(А
{е1, е2}) = r(А ![]() {e1}
{e1}![]() {е2})
{е2}) ![]() r(А
r(А![]() {е1})+ r(A
{е1})+ r(A![]() {е2}) - r((A
{е2}) - r((A![]() {e1})
{e1}) ![]() (A
(A ![]() {е2})) = r(A) + r(A) - r(A) = r(А).
{е2})) = r(A) + r(A) - r(A) = r(А).
2.7.5. Жадный алгоритм
Пусть имеются
конечное множество Е, |Е| = n, весовая функция w: Е![]() R+ и семейство e
R+ и семейство e![]() 2Е.
2Е.
Рассмотрим
следующую задачу: найти X![]() e, такое что
e, такое что
![]() , где
, где ![]()
Другими словами, необходимо выбрать в указанном семействе подможество наибольшего веса.
Не ограничивая
общности, можно считать, что w(e1) ![]() …
…![]() w(en) > 0
w(en) > 0
Рассмотрим следующий алгоритм.
Алгоритм 2.2. Жадный алгоритм
Вход: множество Е = {е1 , . . . , еn}, семейство его подмножеств e и весовая функция w
Множество Е упорядочено в порядке убывания весов элементов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.