Анализ конструктивных фракталов

Глава 4. Анализ конструктивных фракталов

4.1. Инвариантные преобразования

Фракталы можно определить как множества точек, инвариантных относительно полугруппы сжатий.

В самом простом случае сжатие – это масштабное уменьшение с вращением или без него и задается линейным преобразованием плоскости :

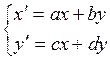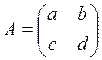,                                                         (4.1)

Преобразование (4.1) с матрицей  будем для краткости обозначать буквой . При

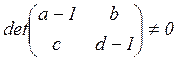                                                                         (4.2)

преобразование (отображение плоскости в себя) имеет единственную неподвижную точку , .

Тип неподвижной точки  определяют корни характеристического уравнения

,                                                        (4.3)

или

.                                                             (4.4)

1)  В случае ,  точка  – устойчивая;

2)  при ,  – седловая (гиперболическая);

3)  при  – эллиптическая;

4)  при ,  – неустойчивая.

Говорят, что отображение  сохраняет площадь, если . Поэтому, когда , то отображение  сохраняет площадь. Сохраняющее площадь отображение может иметь лишь точки эллиптического или гиперболического типа.

Можно рассматривать произведение двух или большего числа отображений . Например, если точка  под действием отображения  переходит в точку , а точка , в свою очередь, переходит в точку , то мы можем записать ,  или .

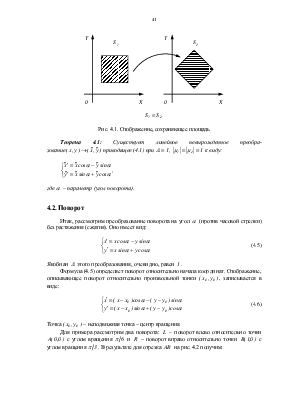
Рассмотрим подробнее отображение, сохраняющее площадь.

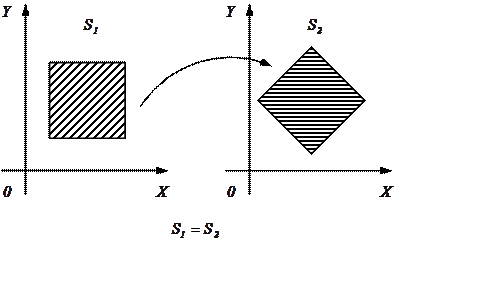
Рис. 4.1. Отображение, сохраняющее площадь

Теорема 4.1: Существует линейное невырожденное преобразование приводящее (4.1) при ,  к виду:

,

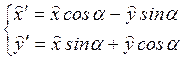где  – параметр (угол поворота).

4.2. Поворот

Итак, рассмотрим преобразование поворота на угол  (против часовой стрелки) без растяжения (сжатия). Оно имеет вид:

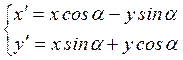                                                                      (4.5)

Якобиан  этого преобразования, очевидно, равен .

Формула (4.5) определяет поворот относительно начала координат. Отображение, описывающее поворот относительно произвольной тонки , записывается в виде:

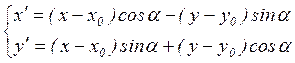                                               (4.6)

Точка  – неподвижная точка – центр вращения.

Для примера рассмотрим два поворота:  – поворот влево относительно точки  с углом вращения  и  – поворот вправо относительно точки  с углом вращения . В результате для отрезка  на рис. 4.2 получим:

, так как , ;

, так как , .

Заметим, что  и  параллельны и повернуты относительно  на .

Формально имеем

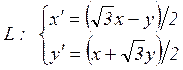
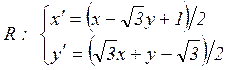                                               (4.7)

Рис. 4.2. Сочетание двух вращений

Поэтому получаем

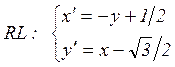
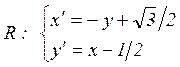                                                           (4.8)

Следовательно,  и  являются поворотом на . Положения центров вращения для  и  соответственно равны ; .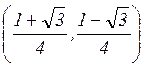

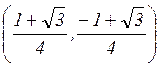4.3. Сжатие (растяжение)

Сжатие (растяжение) связано с изменением масштаба. Перемасштабирование или центральное расширение характеризуется центром и показателем сжатия «». Так, центральное расширение (сжатие), то есть расширение (сжатие) относительно начала координат, выражается соотношениями

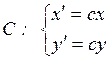,                                                                       (4.9)

а центральное расширение (сжатие) относительно точки  – формулами

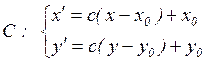.                                                    (4.10)

При  преобразование  определяет растяжение, а при  – сжатие. Для фракталов обычно имеем . При  говорят об отражении, оно соответствует повороту относительно точки  на .

4.4. Поворот с растяжением (сжатием)

Самым важным преобразованием подобия является поворот, скомбинированный с центральным расширением (сжатием). Определяющими характеристиками являются центр и показатель масштабирования. Поворот с расширением – это произведение преобразований:  или . Здесь порядок преобразований не имеет значения.

Рис. 4.3. Преобразование «поворот–растяжение»

Преобразование «поворот–растяжение» относительно начала координат  имеет вид:

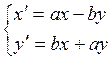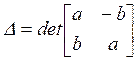,                                                                   (4.11)

Величина  характеризует величину растяжения-сжатия. При  имеем растяжение, а при  – сжатие. В координатах преобразование «поворот–растяжение» показано па рис. 4.4. Точка  с координатами  переходит в точку  с координатами . При этом масштабный множитель . Угол вращения  удовлетворяет соотношениям:

, .

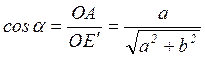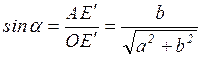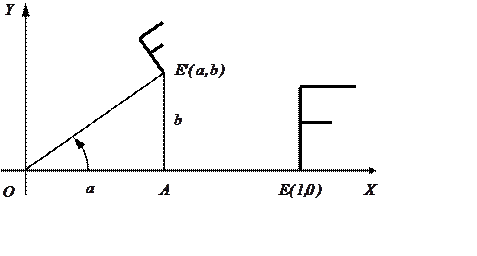
Рис. 4.4. Преобразование «поворот–растяжение»

Преобразование «поворот–растяжение» относительно произвольного центра записывается в виде:

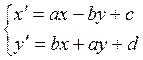                                                      (4.12)

4.5. Применение поворота-сжатия

Рассмотрим кривую Леви. На рис. 4.5 показаны первые фазы ее построения. Фактически приближение фрактала определяется своими вершинами. Поэтому то, что нам нужно сделать, это на каждом шаге найти вершины (и соединить их прямыми линиями). На рис. 4.5 можно обнаружить два поворота-сжатия. Первое преобразование, , имеет центр в точке ,  – угол вращения и  – показатель уменьшения/

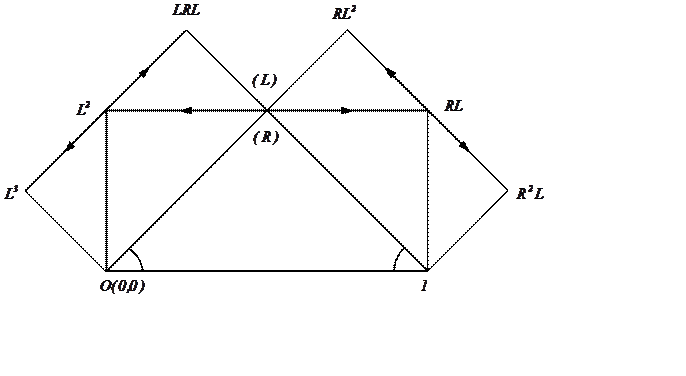
Рис. 4.5. Подобные преобразования во фрактале Леви

Второе преобразование, , имеет центр в точке , угол вращения  и  показатель сжатия . Как , так и  преобразуют вершины в другие вершины так, что фрактал Леви является инвариантным множеством относительно ,  и их комбинаций.

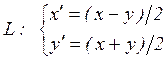
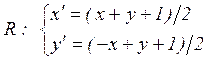                                (4.13)

Из (4.13) следует: , .

Точки фрактала Леви на каждом шаге (фазе)  можно получать, например, подвергая правую точку  последовательности комбинаций преобразований  и . Здесь можно использовать двоичную систему счисления, интерпретируя  как двоичную цифру , a  – как . Таким образом, фрактал состоит из такого же числа точек, сколько чисел между  и  в двоичной системе, а их бесконечное множество

Если мы выберем произвольную точку  в качестве начальной и подвергнем ее преобразованиям  и  несколько раз, то число точек на каждом шаге будет удваиваться. Мы можем изобразить этот процесс в виде дерева с числовыми индексами (рис. 4.6). Например, точка с номером  получится в результате преобразования .

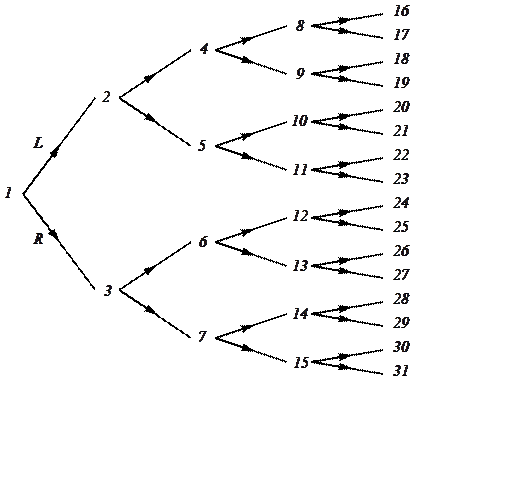
Рис. 4.6. Нумерация двоичного дерева

Если точка  является точкой фрактала, то и все ее итерации, которые получаются из нее, также будут точками фрактала. Это один из способов написания программы для построения вершин фрактала. Этот метод быстрый и эффективный, но требует много машинной памяти.

Есть другой способ, который требует значительно меньше