



Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ГОУВПО «Комсомольский-на-Амуре государственный технический университет»
Кафедра: МОП ЭВМ
Лабораторная работа №2
по дисциплине: «Компьютерное моделирование».
Выполнил: студент группы 4ВС – 1 Алексеенко Н. С.
Проверил: Петров Ю. А.
Комсомольск – на – Амуре
2007
Тема:"Решение линейных дифференциальных уравнений 2-го порядка".
Задание: найти общее решение уравнения, приведя его к каноническому виду:
![]()
Область применения:

Выполнение:
Решим задачу в системе Matlab.
Определим необходимые переменные:
syms dx dy x y teta eta teta_x teta_y eta_x eta_y u_tt u_t u_te u_e u_ee u_x u_y u_xx u_xy u_yy
Общий вид линейного уравнения с частными производными второго порядка с двумя независимыми переменными имеет вид:
![]() (1)
(1)
Зададим коэффициенты уравнения:
a11 = 1; a12 = 1; a22 = 1; b1 = -3; b2 = -3; f = 0; c = 0;
Определим тип уравнения:
a12^2-a11*a22
ans = 0
т.е. уравнение имеет параболический тип.
Данное
условие вытекает из уравнения характеристик ![]() (2).
Оно получается из исходного уравнения (1) с
помощью взаимно - обратного преобразования переменных
(2).
Оно получается из исходного уравнения (1) с
помощью взаимно - обратного преобразования переменных ![]() . Выражая
производные уравнения (1) через переменные
. Выражая
производные уравнения (1) через переменные ![]() ,
получим новые значения для
,
получим новые значения для ![]() .
Подставляя эти производные в уравнение (1),
получим
.
Подставляя эти производные в уравнение (1),
получим ![]() (3).
Вопрос о решении уравнения (3) решается
известными леммами. Так как мы ввели новые переменные с помощью двух, пока
произвольных, соотношений, то можем наложить на их выбор два условия
(3).
Вопрос о решении уравнения (3) решается
известными леммами. Так как мы ввели новые переменные с помощью двух, пока
произвольных, соотношений, то можем наложить на их выбор два условия ![]() . Уравнение
(2) распадается на два дифференциальных уравнения
. Уравнение
(2) распадается на два дифференциальных уравнения 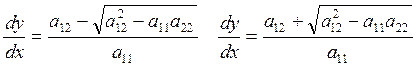 . Знак
подкоренного выражения и определяет тип уравнения (1).
. Знак
подкоренного выражения и определяет тип уравнения (1).
Запишем уравнение характеристик и решим его относительно dy:
v=solve(a11*dy^2-2*a12*dy*dx+a22*dx^2, dy)
v =
[ dx]
[ dx]
Из него определяем функции ![]() и
и ![]() :
:
teta=y-subs(v(1), 'dx', 'x')
eta = y
teta =y-x
eta =y
Определяем первые производные полученных функций:
teta_x=diff(teta, x)
teta_y=diff(teta, y)
eta_x=diff(eta, x)
eta_y=diff(eta, y)
teta_x =-1
teta_y =1
eta_x =0
eta_y =1
Проверяем линейную независимость полученных функций:
det(jacobian([teta;eta],[x,y]))
ans =-1
Определитель матрицы Якоби не
равен нулю, следовательно, ![]() линейно независимы,
т.е. функция
линейно независимы,
т.е. функция ![]() подобрана корректно.
подобрана корректно.
Вычислим производные функции u:
u_x=u_t*teta_x+u_e*eta_x
u_y=u_t*teta_y+u_e*eta_y
u_xx=u_tt*teta_x^2+u_ee*eta_x^2+2*u_te*teta_x*eta_x
u_xy=u_tt*teta_x*teta_y+u_ee*eta_x*eta_y+u_te*(teta_x*eta_y+teta_y*eta_x)
u_yy=u_tt*teta_y^2+u_ee*eta_y^2+2*u_te*teta_y*eta_y
u_x = -u_t
u_y = u_t+u_e
u_xx = u_tt
u_xy = -u_tt-u_te
u_yy = u_tt+u_ee+2*u_te
Подставим полученные производные в исходное уравнение:
a11*u_xx+2*a12*u_xy+a22*u_yy+b1*u_x+b2*u_y+f
ans = u_ee-3*u_e
Мы получили уравнение (1) в
каноническом виде: ![]() . Решение этого уравнения будем
искать в виде
. Решение этого уравнения будем
искать в виде ![]() . Тогда
. Тогда ![]() ,
,
![]()
и ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() . Решим
это уравнение:
. Решим
это уравнение:
d=dsolve('4*D2b-2*Db=0', 'eta')
d = C1+C2*exp(3*eta)
где ![]() ,
, ![]() .
.
Таким образом, решение имеет вид:
![]() . Выполним обратную подстановку и
переобозначим
. Выполним обратную подстановку и
переобозначим ![]() ,
, ![]() :
:
subs(d, eta)
ans = C1+C2*exp(3*y)
Таким образом, решение уравнения
имеет вид: ![]() , где
, где ![]() ,
, ![]() – дважды непрерывно-дифференцируемые
функции. Например, возьмем следующие функции:
– дважды непрерывно-дифференцируемые
функции. Например, возьмем следующие функции:
fun=y-x;
C3=6*fun
C4=fun
C3 = 6*y-6*x
C4 = y-x
u=C3+C4*exp(3*y)
u = 6*y-6*x+(y-x)*exp(3*y)
и подставим их в исходное уравнение:
a11*diff(diff(u, x), x)+2*a12*diff(diff(u, x), y)+a22*diff(diff(u, y), y)+b1*diff(u, x)+b2*diff(u, y)+c*u+f
ans =0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.