Моделирование планетарно-ползунного механизма. Расчетная схема эпи- и гипоциклоидных механизмов

Моделирование планетарно-ползунного механизма

На рис.1 приведена расчетная схема эпи- и гипоциклоидных механизмов. Через R и r обозначены радиусы центрального колеса и сателлита соответственно, размер стержня АВ=l (буква). Тогда проекции точки В стержня на оси x и y декартовой системы координат (в виде вектора X) будут иметь вид:

X₀ = (1+k×i)×cos(f) - l×cos(((1+k×i)/i)×f+k×a) – проекция на ось х,

X₁ = (1+k×i)×sin(f) - k×l×sin(((1+k×i)/i)×f+k×a) – проекция на ось y, где проекции точки В выражены в долях радиуса R центрального колеса:

i=r/R;  l= l/R; Х₀₌xB/R; Х₁=yB/R.

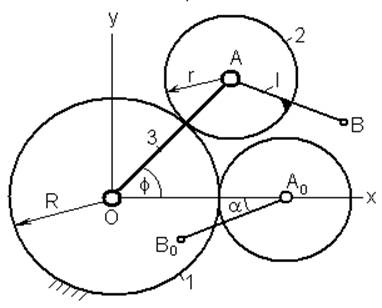
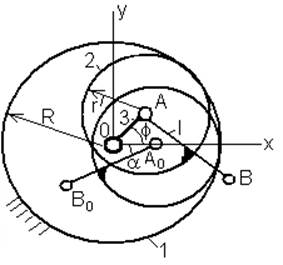
Рис.1. Расчетная схема эпи- и гипоциклоидных механизмов

Знаки ± заменены константой k=+1 для внешнего  и k= - 1 для внутреннего зацепления.

При моделировании планетарных механизмов решим следующие задачи:

1.Исследуем влияние параметров планетарных механизмов на траекторию точки В. На рис. 2 и рис.3 показана единичная окружность (R=1) и траектории точки В для внешнего и внутреннего зацепления в функции от параметра сборки α. 

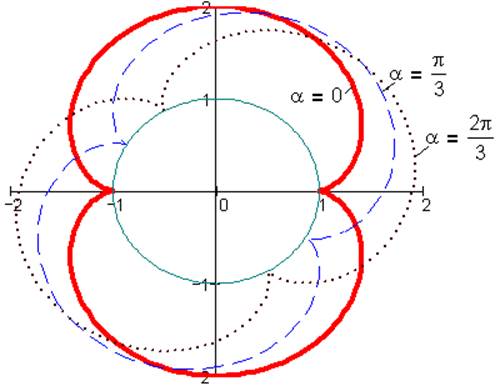
Рис. 2. Эпициклоида при k=1, i=0.5, λ=0.5

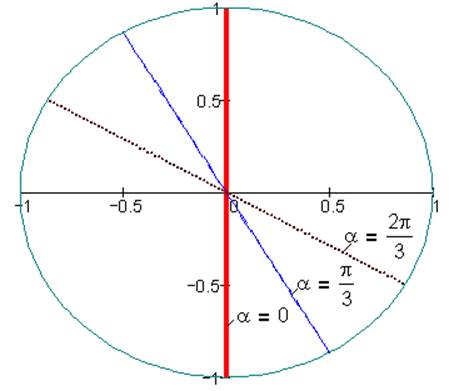
Рис. 3. Гипоциклоида при k= - 1, i=0.5, λ=0.5

Для точек, лежащих на подвижном колесе радиуса r (λ=0.5) при внутреннем зацеплении траектории точек В представляют собой прямые линии. Для точек, лежащих вне подвижной окружности (l>r) траектории точки В – удлиненные эпициклоиды (рис. 4) для внешнего и гипоциклоиды для внутреннего (рис.5) зацепления. Изменение угла α поворачивает циклоидальную кривую вокруг центра начала координат.

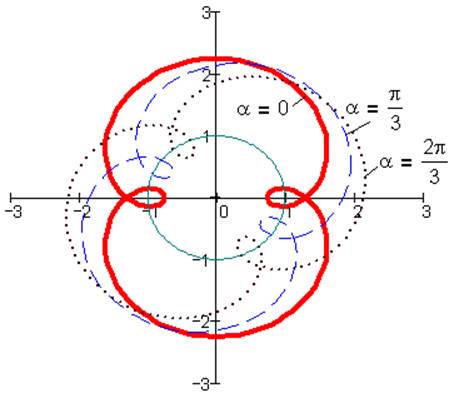
Рис. 4. Эпициклоида при k=1, i=0.5, λ=0.75

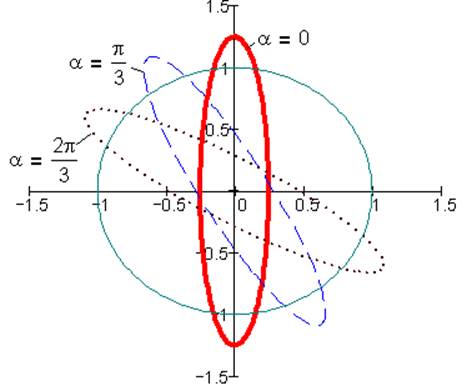
Рис. 5. Гипоциклоида при k= - 1, i=0.5, λ=0.75

Для точек, лежащих внутри подвижной окружности (l<r) траектории точки В – укороченные эпициклоиды (рис. 6) для внешнего и гипоциклоиды для внутреннего (рис.7) зацепления.

Изменение параметра i изменяет число петель траектории.

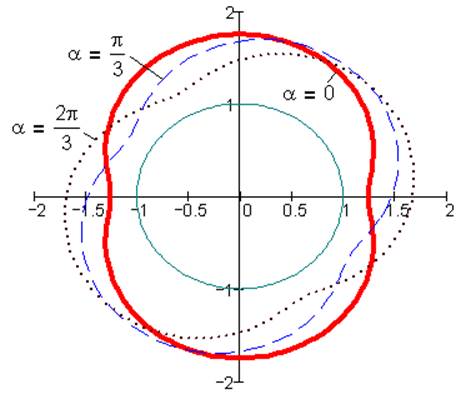
Рис. 6. Эпициклоида при k=1, i=0.5, λ=0.25

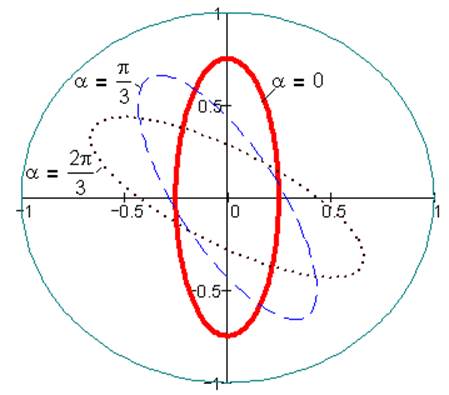
Рис. 7. Гипоциклоида при k= - 1, i=0.5, λ=0.25

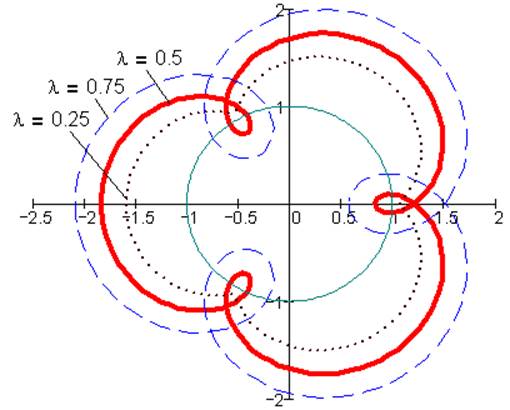
Рис. 7. Эпициклоиды при k=1, i=1/3, α=0

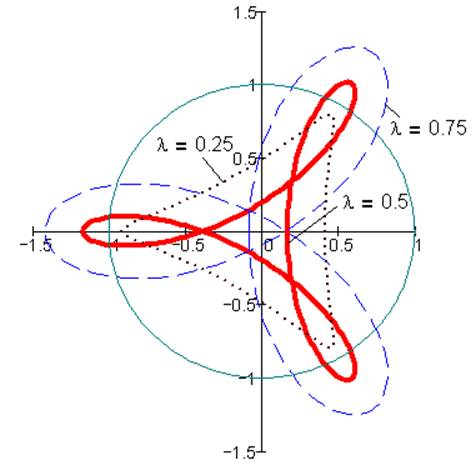
Рис. 8. Гипоциклоиды при k= -1, i=1/3, α=0

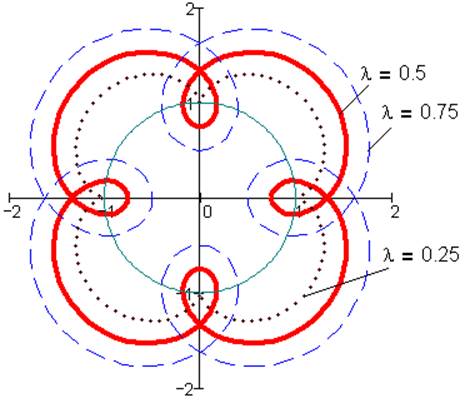
Рис. 9. Эпициклоиды при k= 1, i=1/4, α=0

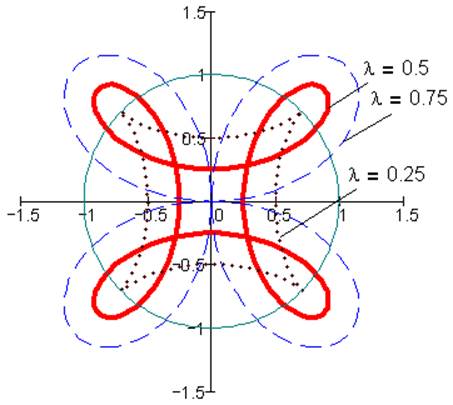
Рис. 10. Гипоциклоиды при k= -1, i=1/4, α=0

1. Присоединим в точке В группу Ассура, состоящую из двух поступательных и одной вращательной пары (2ПВ), рис.11 и постоим диаграммы S₁(φ) и S₂(φ), рис.12 – рис.25.

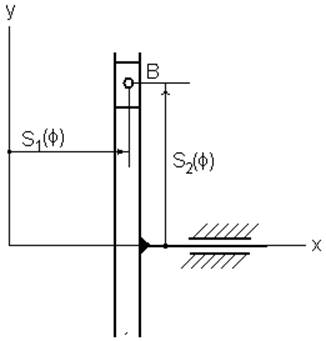
Рис. 11. Прицепная группа Асура 2ПВ

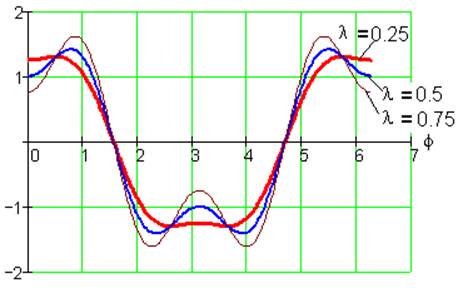
Рис. 12. Функция положения S₁(φ) при k= 1, i=1/2, α=0

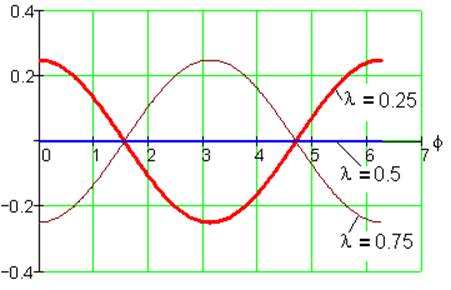
Рис. 13. Функция положения  S₁(φ) при k= -1, i=1/2, α=0

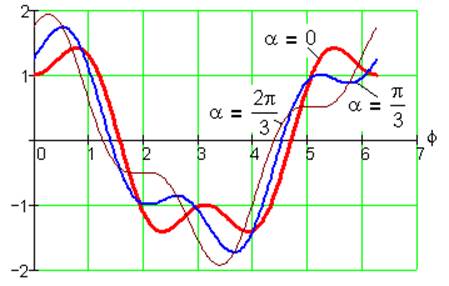
Рис. 14. Функция положения  S₁(φ) при k= 1, i=1/2, λ=0.5

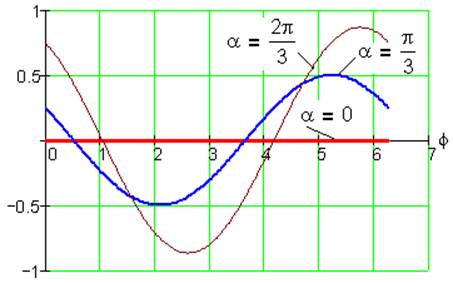
Рис. 15. Функция положения  S₁(φ) при k= -1, i=1/2, λ=0.5

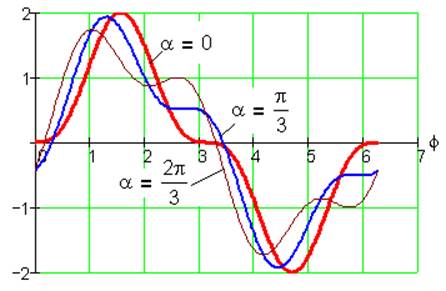
Рис. 16. Функция положения  S₂(φ) при k= 1, i=1/2, λ=0.5

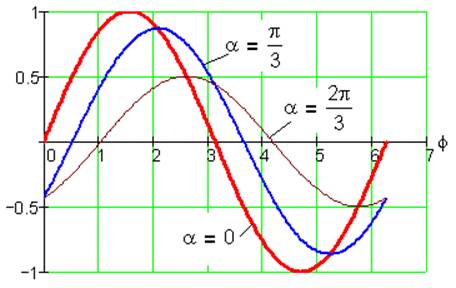
Рис. 17. Функция положения  S₂(φ) при k= -1, i=1/2, λ=0.5

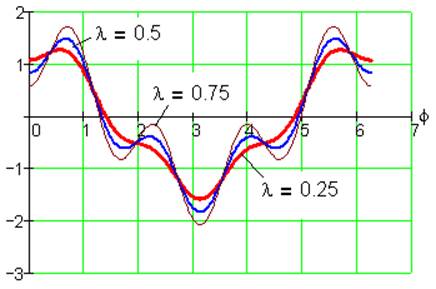
Рис. 18. Функция положения  S₁(φ) при k= 1, i=1/3, α=0

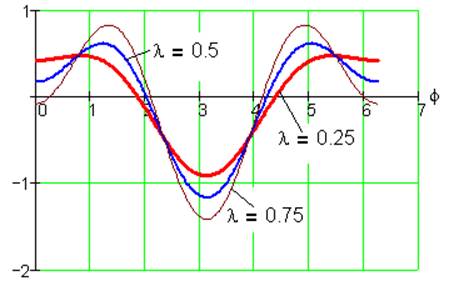
Рис. 19. Функция положения  S₁(φ) при k= -1, i=1/3, α=0

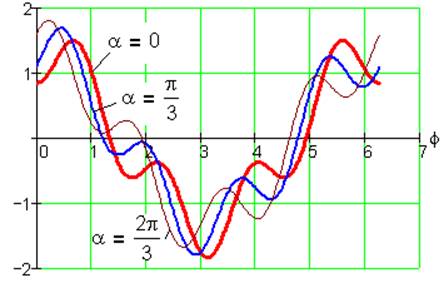
Рис. 20. Функция положения  S₁(φ) при k= 1, i=1/3, λ=0.5

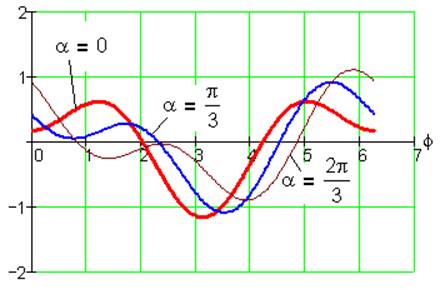
Рис. 21. Функция положения  S₁(φ) при k= -1, i=1/3, λ=0.5

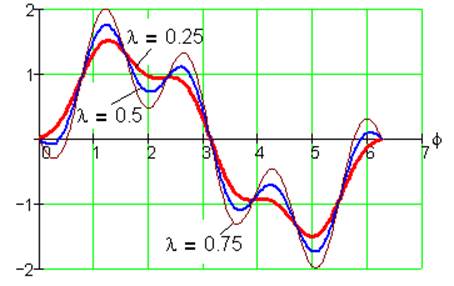
Рис. 22. Функция положения  S₂(φ) при k= 1, i=1/3, α=0

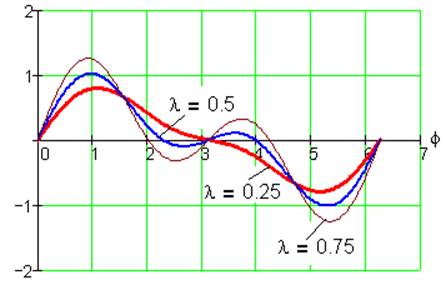
Рис. 23. Функция положения  S₂(φ) при k= -1, i=1/3, α=0

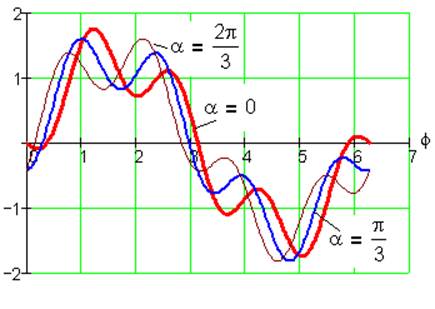
Рис. 24. Функция положения  S₂(φ) при k= 1, i=1/3, λ=0.5

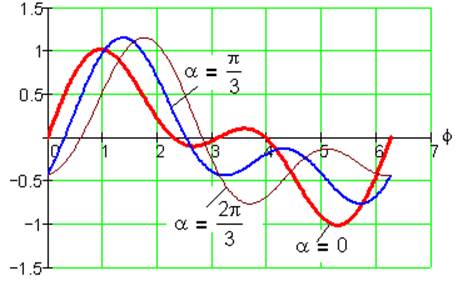
Рис. 25. Функция положения  S₂(φ) при k= -1, i=1/3, λ=0.5

2. Присоединим в точке В группу Ассура, состоящую из двух вращательных и одной поступательной пары (2ВП), рис.26 и постоим диаграммы ζ(φ) и S(φ), рис.12 – рис.25.

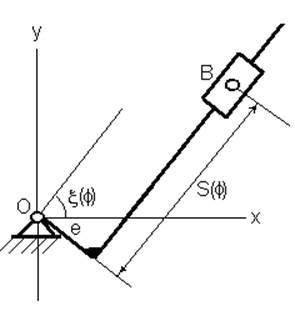
Рис. 26. Прицепная группа Асура 2ВП