по курсу «Компьютерное моделирование»
Выполнили: Алексеенко Н. С.
Проверил: Петров Ю.А.
Вариант: 1
Комсомольск-на-Амуре
Тема: «Моделирование планетарно-ползунного механизма».
Цель работы: Изучить планетарно-ползунный механизм.
Задание: Произвести моделирование планетарно-ползунного механизма, построить математическую модель с помощью интегрированной среды MathCAD, проанализировать полученные результаты.
Моделирование планетарно-ползунного механизма
На рис.1 приведена расчетная схема эпи- и гипоциклоидных механизмов. Через R и r обозначены радиусы центрального колеса и сателлита соответственно, размер стержня АВ=l. Тогда проекции точки В стержня на оси x и y декартовой системы координат (в виде вектора X) будут иметь вид:
X0 = (1+k×i)×cos(f) - l×cos(((1+k×i)/i)×f+k×a) – проекция на ось х,
X1 = (1+k×i)×sin(f) - k×l×sin(((1+k×i)/i)×f+k×a) – проекция на ось y, где проекции точки В выражены в долях радиуса R центрального колеса:
i=r/R; l= l/R; Х0=xB/R; Х1=yB/R.
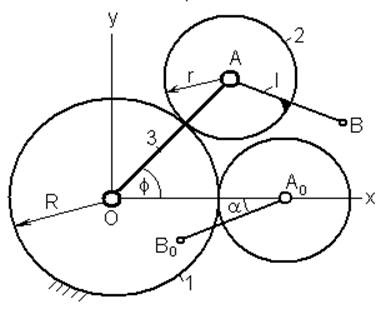
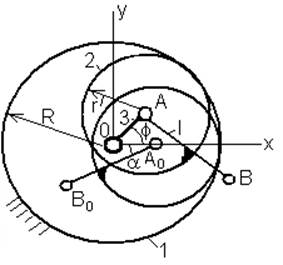
Рис.1. Расчетная схема эпи- и гипоциклоидных механизмов
Знаки ± заменены константой k = +1 для внешнего и k = -1 для внутреннего зацепления.
При моделировании планетарно-ползунного механизма решим следующие задачи:
- Исследуем влияние параметров планетарных механизмов на траекторию точки В.
- Исследуем влияние параметров планетарных механизмов на траекторию точки Е.
Присоединим к точке В группу Ассура (см. рис. 2).

Рис.2. Прицепная группа
Введем параметры группы Ассура: ε=e/R, m=L/R, q=ρ/R
Обозначим координаты x и y точек C, D и E через:
Х0=xB/R; Х1=yB/R;
Х2=xC/R; Х3=yC/R;
Х4=xD/R; Х5=yD/R;
Х6=xE/R; Х7=yE/R;.
Для описания характеристик планетарно-ползунного механизма используем функцию:
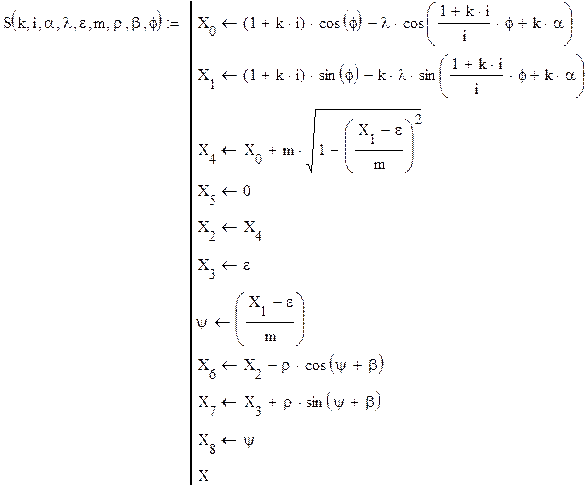
Данная функция возвращает вектор значений (X0, X1, X2, X3, X4, X5, X6, X7, X8), где
X0 – проекция точки B ось х
X1 – проекция точки B ось y
X2 – проекция точки C ось x
X3 – проекция точки C ось y
X4 – проекция точки D ось x
X5 – проекция точки D ось y
X6 – проекция точки E ось x
X7 – проекция точки E ось y
X8 – значение угла ψ.
Исследуем влияние параметров планетарных механизмов на траекторию точки В.
Построим графики траекторий точки В, для чего введем две новые функции:
|
|
|
функция для описания внешнего сцепления дисков |
|
|
|
функция для описания внутреннего сцепления дисков |
Начальные параметры функций определяются следующим образом:
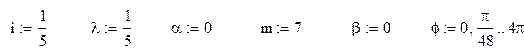
Проследим, как меняется траектория точки В при изменении угла сборки α:
Для внешнего зацепления получаем график, представленный на рис.1. Из графика видно, что при изменении угла сборки α график поворачивается по часовой стрелке на указанный угол.
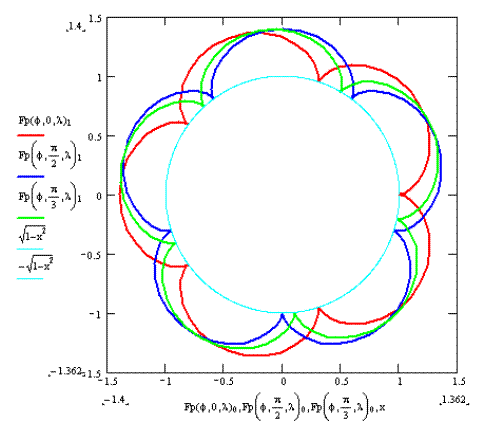
Рис. 1.
Для внутреннего зацепления получаем график, представленный на рис.2. Из графика видно, что при изменении угла сборки α график поворачивается против часовой стрелки на указанный угол.
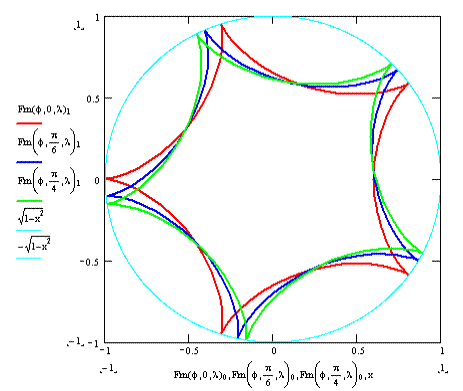
Рис. 2.
При уменьшении параметра λ (радиус большего диска увеличивается по отношению к стержню AB) графики как внешнего, так и внутреннего зацеплений постепенно видоизменяются, приобретая более плавные очертания, приближаясь по виду к окружности. (Рис. 3, Рис. 4.)
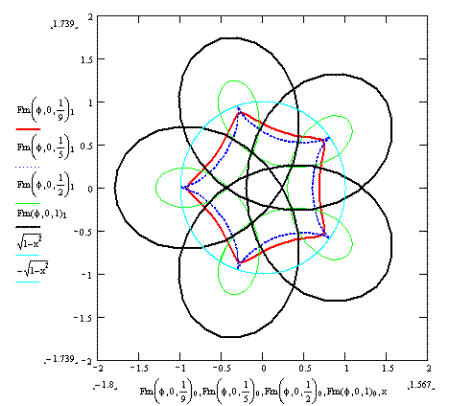
Рис. 3.
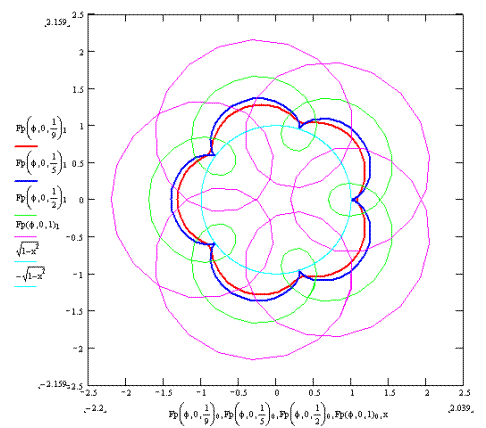
Рис. 4.
Соответственно при увеличении параметра λ (радиус большего диска уменьшении по отношению к стержню AB) графики как внешнего так и внутреннего зацеплений постепенно видоизменяются, приобретают более извилистые очертания. Для внешнего зацепления траектория движения точки В начинает попадать в пределы единичной окружности. Для внутреннего зацепления наоборот, траектория движения точки В начинает выходить за пределы единичной окружности. (Рис. 3, Рис. 4.)
Рассмотрим параметры прицепной группы Ассура.
Для этого введем функции:
|
|
|
функция для описания внешнего сцепления дисков |
|
|
|
функция для описания внутреннего сцепления дисков |
Начальные параметры функции определяются следующим образом:
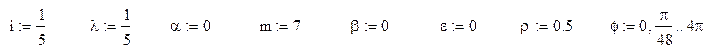
В процессе работы координата x точки D изменяется в соответствии с графиком, представленным на Рис. 5.
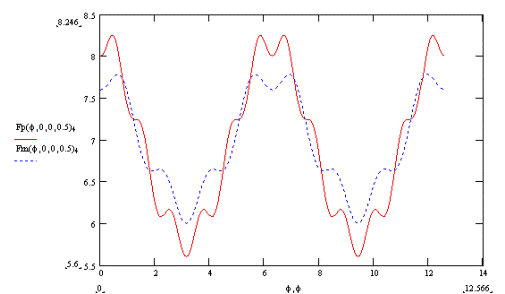
Рис. 5.
Исследуем влияние параметров планетарного механизма (β, ρ и ε) на траекторию точки Е.
При изменении параметра ρ (относительная длина стержня СЕ) координата х точки Е изменяется согласно графику на рис. 6. Видно, что чем меньше ρ, тем больше становится x.
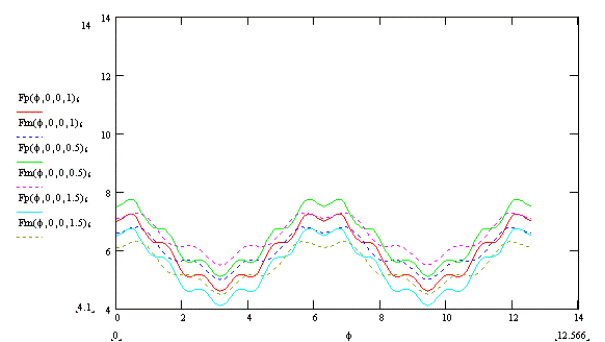
Рис. 6.
При изменении параметра ρ координата у точки Е изменяется согласно графику на рис. 7. График становится все более "скачкообразным" с увеличением ρ.
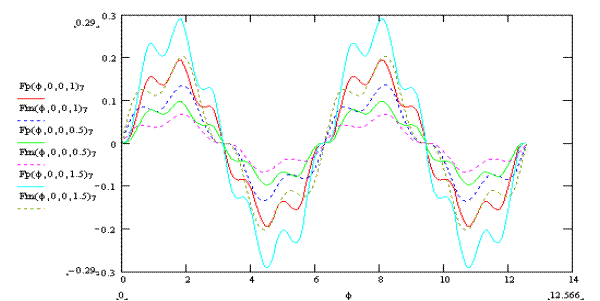
Рис. 7.
Траектория движения точки Е выглядит следующим образом (рис. 8.).
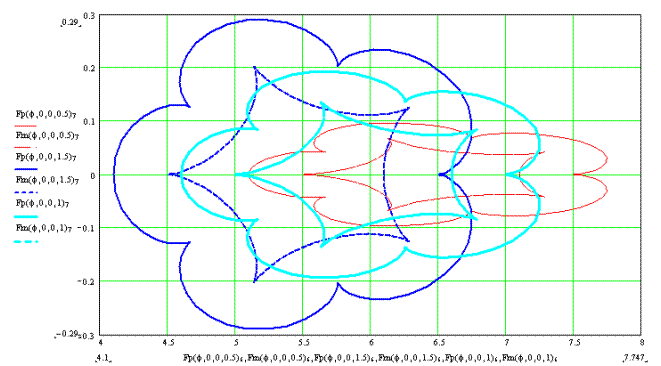
Рис. 8.
Можно заметить, что траектория сходна с траекторией движения точки В, как для внешнего, так и для внутреннего зацепления, но при меньшем ρ график сдвигается вправо по оси Ох и становится более узким в высоту.
При изменении параметра β координата х точки Е изменяется согласно графику на рис. 9. При большем угле β проекция точки В на ось Ох находится ближе к точке D, поэтому координата х будет больше, график сдвигается по оси Oy вверх.
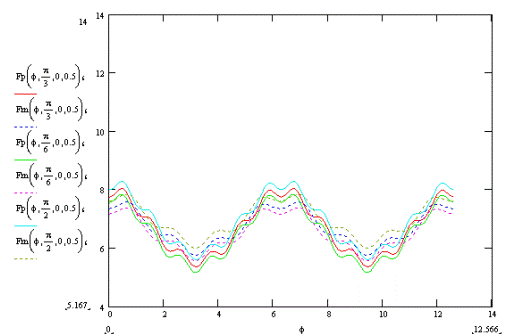
Рис. 9.
При изменении параметра β координата у точки Е изменяется согласно графику ни рис. 10. При меньшем угле β проекция точки В на ось Оу находится ближе к 0, поэтому координата у будет меньше, и график для меньших β будет менее выпуклый?????.
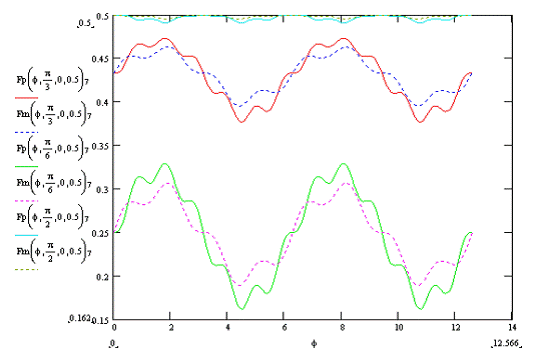
Рис. 10.
Траектория движения точки Е выглядит следующим образом (рис. 11.).
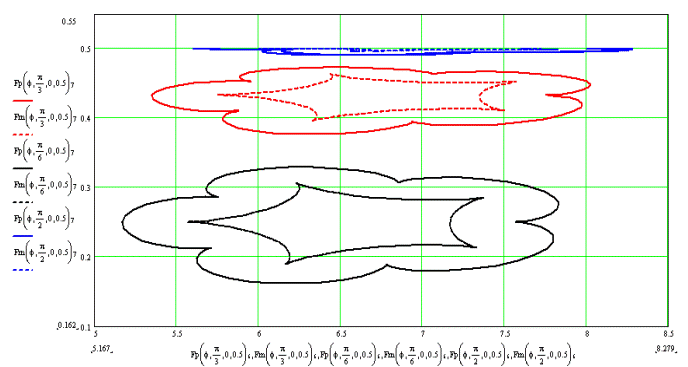
Рис. 11.
При изменении параметра ε (длина CD) координата х точки Е изменяется согласно графику ни рис. 12.??????????????????????????????????? зафига?????????????????????????????
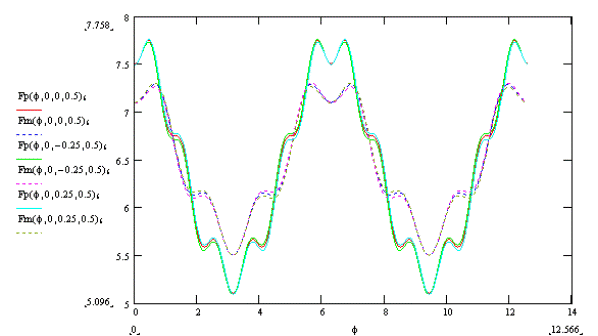
Рис. 12.
При изменении параметра ε координата у точки Е изменяется согласно графику ни рис. 13. Очевидно, чем больше параметр ε, тем координата у точки Е больше, а график расположен выше.
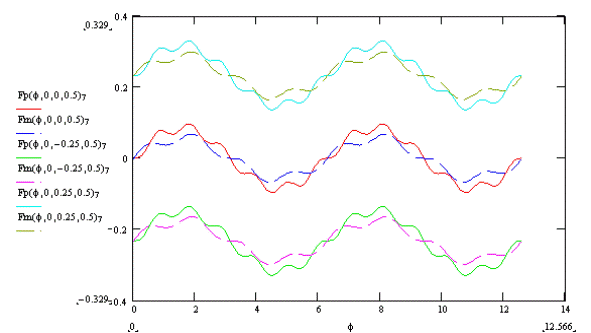
Рис. 13
Траектория движения точки Е выглядит следующим образом (Рис. 14). Чем больше параметр ε, тем координата у точки Е больше, а график расположен выше.
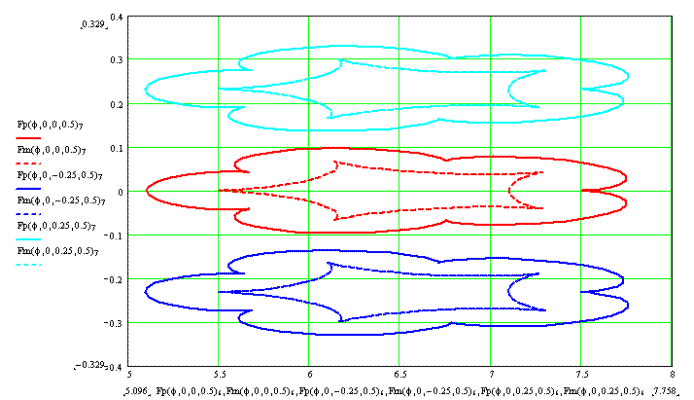
Рис. 14.
Список использованных источников
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.