![]() Построенная
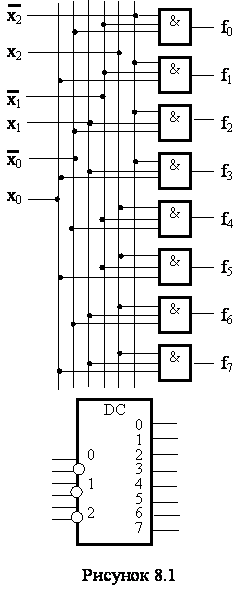
по этим уравнениям схема (см. рисунок 8.1) представляет собой восемь
независимых трехвходовых схем И. Прямые и инверсные значения разрядов кода
могут сниматься с прямых и инверсных выходов регистра или счетчика. Недостатком
такой схемы дешифратора является прямая зависимость числа входов схем И от
разрядности входного кода, что приводит к технологическим трудностям реализации
элементов в виде микросхем. Если построить линейный дешифратор на логических
элементах с небольшим числом входов, то это приведет к резкому увеличению их
числа. Например, если построить приведенную на рисунке 8.1 схему на элементах
И на два входа, то их потребуется в два раза больше, так
как
Построенная
по этим уравнениям схема (см. рисунок 8.1) представляет собой восемь
независимых трехвходовых схем И. Прямые и инверсные значения разрядов кода
могут сниматься с прямых и инверсных выходов регистра или счетчика. Недостатком
такой схемы дешифратора является прямая зависимость числа входов схем И от
разрядности входного кода, что приводит к технологическим трудностям реализации
элементов в виде микросхем. Если построить линейный дешифратор на логических
элементах с небольшим числом входов, то это приведет к резкому увеличению их
числа. Например, если построить приведенную на рисунке 8.1 схему на элементах
И на два входа, то их потребуется в два раза больше, так
как
![]() В
общем случае, если преобразовать исходную систему логических уравнений к виду
В
общем случае, если преобразовать исходную систему логических уравнений к виду
то можно получить схему дешифратора пирамидального вида на двухвходовых логических элементах, при этом уменьшив их общее количество по сравнению с количеством элементов, необходимых для построения линейного дешифратора.
![]()
 В
качестве примера, построим пирамидальный дешифратор на четыре входа и шестнадцать
выходов, работа которого описывается системой уравнения
типа .
В
качестве примера, построим пирамидальный дешифратор на четыре входа и шестнадцать
выходов, работа которого описывается системой уравнения
типа .
Схема приведена на рисунке 8.2.
Недостатком схемы является ее многоступенчатость, что приводит к увеличению как аппаратурных затрат, так и времени срабатывания.
![]() Поэтому
часто на практике строят линейно-матричные дешифраторы с использованием
двухвходовых логических элементов. Общее количество элементов для построения
таких дешифраторов требуется меньше, чем для пирамидальных дешифраторов.
Принцип построения таких дешифраторов состоит в разбиении исходных логических
функций на группы, в которых содержится от двух до n/2 переменных.
Пусть исходные уравнения разбиты на две группы
Поэтому
часто на практике строят линейно-матричные дешифраторы с использованием
двухвходовых логических элементов. Общее количество элементов для построения
таких дешифраторов требуется меньше, чем для пирамидальных дешифраторов.
Принцип построения таких дешифраторов состоит в разбиении исходных логических
функций на группы, в которых содержится от двух до n/2 переменных.
Пусть исходные уравнения разбиты на две группы
![]() Обозначим первую группу переменных через Аq,
а вторую группу - через Вq.Тогда
Обозначим первую группу переменных через Аq,
а вторую группу - через Вq.Тогда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.