Порядок расчета стержневой системы методом конечных элементов. Порядок расчета моментов инерции сложного сечения, страница 2

19.Определяются узловые перемещения элементов  в глобальных осях координат путем сопоставления с матрицей индексов перемещений элементов .

20.Определяются узловые перемещения элементов в локальных осях координат .

21.Снова используется основное уравнение МКЭ. Определяются узловые усилия в каждом элементе в локальных осях координат .

22.Решается задача сопротивления материалов. Из условия прочности для каждого элемента подбираются размеры поперечного сечения. Определяется масса конструкции.

Динамический расчет

23.Вручную вводится сосредоточенная масса в заданном узле.

Далее вновь компьютерный расчет.

24.Формируется матрица масс системы с учетом сосредоточенной массы.

25.С помощью функций genvals и genvecs решается уравнение свободных незатухающих колебаний  и рассчитывается вектор собственных частот и спектр собственных векторов системы.

26.Используя прямое интегрирование матричного уравнения вынужденных затухающих колебаний  методом конечных разностей (по Ньюмарку) рассчитывается динамическое перемещение одного из узлов системы в момент резонанса на первой собственной частоте и находится коэффициент динамичности.

Вновь работа расчетчика

27.Уточнить форму и размеры сечений с учетом соблюдения условий прочности и жесткости и для достижения минимального веса конструкции.

28.Произвести повторный расчет стержневой системы несколько раз до достижения нужных результатов.

29.Для элемента, нагруженного распределенной нагрузкой, из внутренних усилий вычесть эквивалентные нагрузки, вернуть на элемент распределенную нагрузку, построить эпюры внутренних усилий, определить максимальное эквивалентное напряжение.

30.Рассчитать вручную заданные преподавателем коэффициенты жесткости а)стержневой системы, б)сложного поперечного сечения (при решении уравнения Пуассона).

31.По результатам расчета нарисовать вид стержневой системы после деформации.

Порядок расчета моментов инерции сложного сечения

Работа расчетчика

1.  Ввести матрицу координат контура сложного сечения.

2.  Для создания сетки конечных элементов планшетным методом указать число рядов и число столбцов планшета.

Работа компьютерной программы

3.  С использованием функций интерполяции определяются уравнения контура сечения.

4.  По формулам сопротивления материалов определяются осевые моменты инерции сложного сечения.

5.  По заданному числу рядов и столбцов формируется планшет для разбивки сечения на конечные элементы.

6.  Определяются координаты узлов планшета и сложного сечения.

7.  Формируется матрица индексов планшета и сложного сечения путем исключения узлов планшета, находящихся за пределами сложного сечения.

8.  Записываются граничные условия — список узлов, лежащих на контуре сложного сечения.

9.  С использованием уравнения Пуассона 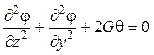, сведенного к основному уравнению , формируется матрица жесткости элементов .

10.Рассчитывается матрица жесткости системы  путем суммирования коэффициентов жесткости элементов по матрице индексов узлов.

11.Формируется вектор правых частей уравнений 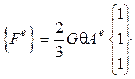, для чего надо задать любое значение относительного угла закручивания . Например, .

12.Учитываются граничные условия (перечень узлов на контуре сечения).

13.Решается основное уравнение  и находится вектор узловых значений функции напряжений .

14.Рассчитываются касательные напряжения в узлах и крутящий момент в сечении.

15.Определяется момент инерции  и момент сопротивления при кручении .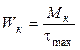

16.Найденные моменты инерции вводятся в программу расчета стержневой системы.

17.В программе расчета стержневой системы строятся эпюры внутренних усилий для стержня сложного поперечного сечения. Определяется максимальное эквивалентное напряжение для этого стержня.

18.Используя масштабный коэффициент, надо увеличить или уменьшить размеры сложного сечения с целью удовлетворения условиям прочности и жесткости.