Рис.7. Принцип принятия решения при поиске синхросигналов слов: а - символы фаз; б - решение по сумме единиц; в - решение исключением фаз с информационными символами считывание записанного числа в многоканальный счетчик. Затем регистр обнуляется и заполняется следующими n символами кода и т.д. Через т слов в одном из каналов счетчика будет т единиц, а в остальных - числа, меньшие т, т.к. в них попали информационные символы, принимающие значение нуля. Достижение суммой величины т обнаруживается пороговым устройством.
Сигнал схем сравнения можно записать в регистр. Если последовательность нулей и единиц, записанных в регистре, выдавать последовательно с частотой символов fТ, то появившаяся единица будет канальным синхроимпульсом.
 |
Рис.8. Структурная схема поиска сигналов синхронизации слов по алгоритму с накоплением синхросимволов
Определим необходимую продолжительность накопления т для обнаружения канальных синхросигналов. Вначале предположим, что искажения сигналов отсутствуют. В этом случае пропуска сигнала быть не может, т.к. по крайней мере в одном канале счетчика, соответствующем последовательности канальных синхросигналов, будет накоплено т единиц. В то же время ложные синхроимпульсы могут появиться, так как существует некоторая вероятность накопления последовательности m единиц информационных сигналов в каком-либо счетчике. Оценим эту вероятность, определяющую вероятность ложной синхронизации.
Предположим, что вероятности появления нулей и единиц на произвольной позиции в слове одинаковы: Р(0) = Р(1) = 1/2.
Вероятность появления ложного синхросигнала на выходе произвольного канала порогового устройства можно определить как вероятность появления подряд m единиц, т.е. 0,5т . Если информационных разрядов n - 1 , то вероятность ложной синхронизации определяется суммой вероятностей появления ложных синхросигналов во всех информационных разрядах:
РЛ.С. » 2-т (n-1). (2)
Если задана вероятность ложной синхронизации, то можно вычислить необходимое число анализируемых слов:
m = log 2 {(n - 1)/РЛ.С.)}. (3)
При воздействии помех возможны ошибки: ошибочный прием единицы вместо нуля и наоборот. Будем считать эти события равновероятными. Вероятность искажения символа, т.е. трансформации 1®0 и 0®1, называют вероятностью ошибки р .
Вероятность появления единицы в любом информационном разряде
Р1 = Р(1)(1-р) + Р(0)р.
где Р(0) и P(1) - априорные вероятности появления нуля и единицы.
Если Р(0) = Р(1)= 0,5, то Р1 = 0,5.
Таким образом, при наличии помех ситуация ничем не отличается от рассмотренной ранее для случая отсутствия помех. В связи с этим для определения вероятности ложной синхронизации может быть использована формула (2).
В синхроразряде без помех появляются только единицы Р(1)=1. В случае помех возможна трансформация единицы в нуль с вероятностью р. Поэтому установление порога, равного m единиц, будет приводить к пропуску в обнаружении синхросигнала вследствие пропадания некоторых из этих m единиц. Вероятность пропуска можно уменьшить путем уменьшения порога счета l<m.
Если порог счета выбран равным l < m , то вероятность пропуска равна вероятности пропадания не менее m - l+ 1 синхросимволов за т циклов счета, или, что то же самое, вероятности. появления не больше чем l - 1 синхросимволов за т циклов. Вероятность появления ровно i ошибок за т циклов определяет вероятность пропадания i единиц
РПРi = Стi рi (1 - р)т-i, (4)
где Стi - биномиальные коэффициенты, равные
С учетом сказанного выше вероятность пропуска равна сумме вероятностей пропадания (m - l+ 1)-го, (m - l+ 2)-го, ..., m-го сигналов:
РПР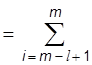 
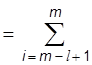РПРi Стi рi (1 - р)т-i. (5)
С другой стороны, вероятность ложной синхронизации
РЛ.С.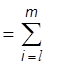 
Стi Рi (1) (1
- Р(1))т-i =2-т
Стi . (6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.