Математическая модель функционирования артиллерийских автоматов с отводом пороховых газов, страница 2

Таким образом, разработка таких моделей представляет самостоятельную задачу. А результаты ее решения могут быть интегрированы в современные прикладные программы баллистических расчетов.

Из рассмотрения циклограммы работы механизмов автоматики пушки АМ-23 следует, что придвижении затворной рамы назад совершаются следующие операции перезаряжания:

-  свободный ход затворной рамы;

-  открывание затвора и первый этап экстракции гильзы;

-  разворот рычага экстрактора-досылателя для подготовки его к встрече с упором ствольной коробки;

-  второй этап экстракции гильзы (при работе ускорительного механизма);

-  рабочий ход каретки подачи;

-  торможение затворной рамы газовым буфером.

В данной задаче рассматриваются только принципиальные моменты составления уравнения движения затворной рамы в характерные этапы ее движения.

1.  Период открывания затвора и начального этапа экстракции гильзы

Коэффициенты передачи сил от i-х звеньев к основному звену на данном этапе определяются по зависимостям

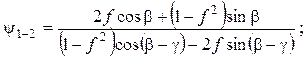
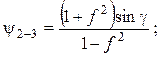
где ¦ - коэффициент трения скольжения; g - угол наклона опорной поверхности затвора к зеркалу; b - угол наклона копира затворной рамы.

Передаточное отношение звеньев определяются по зависимостям

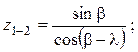
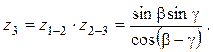
1 основное звено – затворная рама;

2 звено – затвор в прямолинейном поступательном движении относительно ствольной коробки;

3 звено – экстрактор-досылатель и гильза в прямолинейном поступательном движении относительно ствольной коробки.

Дифференциальное уравнение движения основного звена определяются по формуле (  )

                   ( )

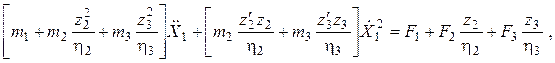где m₁ – масса затворной рамы с учетом присоединенной 1/3 массы пружины; m₂ – масса затвора в поступательном движении относительно ствольной коробки; m₃ – масса экстрактора-досылателя в месте с гильзой в поступательном движении относительно затворной рамы;

где F_пр – усилие возвратных пружин затворной рамы; F₁ – сумма всех внешних сил, приложенных к основному звену; F₂=0; F₃= F_г, где F_г – усилие извлечения гильзы из патронника.

Усилие извлечения гильзы из патронника F_г определяется зависимостью

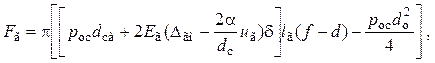
где  - остаточное давление пороховых газов;  - внутренний диаметр элемента гильзы;  - модуль упругости материала гильзы;  - начальный относительный натяг гильзы;  - угол наклона первого (основного) конуса гильзы;  - средний внутренний диаметр гильзы;  - перемещение фланца гильзы от начального положения;  - толщина стенки гильзы;  - длина первого (основного) конуса гильзы;  - коэффициент трения скольжения;  - диаметр дна гильзы.

Настоящая зависимость определена при следующих допущениях:

-   величина относительного натяга  постоянна по всей длине гильзы;

-  пренебрегаем влиянием радиальных напряжений в материале гильзы на величину тангенциальных деформаций;

-  деформация патронника отсутствует;

-  принимаем толщину стенок гильзы постоянной по всей ее длине и равной среднему ее значению;

-  при экстракции гильзы все сечения ее перемещаются вдоль оси на одинаковую величину (равносильно пренебречь осевыми напряжениями ).

2.  Период работы ускорительного механизма экстракции гильзы

1-e основное звено - затворная рама;

2-ое условное звено - рычаг экстрактора-досылателя в угловом перемещении относительно его оси на затворной раме;

3-е условное звено -экстрактор-досылатель и гильза в прямолинейном поступательном перемещении относительно ствольной коробки.

Дифференциальное уравнение движения затворной рамы в рассматриваемый период

                   ( )

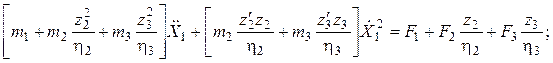где -момент инерции рычага экстрактора-досылателя;

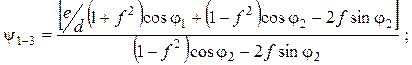
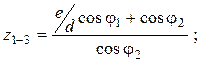
3.  Период рабочего хода каретки механизма подачи патронов

Сила сопротивления патронной ленты

Усилие на толкателе каретки подачи

Допущение: не учитывают зазоры и силы сопротивления, действующие на звенья. Примем схему, в которой масса патронов и звеньев считаем равномерно распределенной. Влияние соответствующей ленты учтем добавлением к найденному усилию проекции веса части ленты, расположенной ниже данного сечения.

Усилие, где  - усилие в ленте;  - жесткость звена ленты; m – масса элемента(патрона со звеном);  - скорость ведомого конца ленты.

Учитывая вес свисающей части ленты, получим для ведомого конца

где n – число патронов в наклонной части ленты; q – угол наклона подводящего рукава к горизонту.

Усилие в ленте с учетом сопротивления определяется по зависимости

где  - перемещение ведущего конца ленты; С_л – жесткость одного звена патронной ленты; 2h – коэффициент, определяемый опытным путем для учета потерь энергии, идущей на преодоление различных сопротивлений.

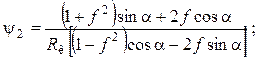
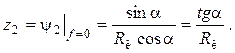
4.   Период торможения затворной рамы газовым буфером

При встрече затворной рамы с поршнем газового буфера (рис. 1.) происходит ударное присоединение неподвижного звена к основному. При этом скорость основного звена приобретает значение

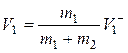
где  - масса затворной рамы;  - масса поршня газового буфера;  - скорость затворной рамы при ее подходе к газовому буферу.

Коэффициент восстановления скорости принимаем , считая связь абсолютно неупругой.

Изменение давления газа в газовом буфере принимаем по политропическому закону, т.е.

где  - текущие значения давления и объема газа;  - начальные их значения;         n – показатель политропы.

Отсюда следует .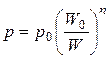

Текущее значение объема газа в цилиндре газового буфера определяется формулой

где  - рабочая площадь поршня.

Сила торможения газового буфера

Сила  также будет воздействовать на затворную раму при ее движении вперед на начальном этапе.

5.  Период досылки патрона при работе ускорительного механизма

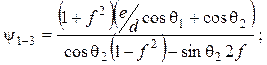
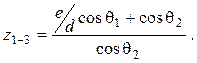
6.  Период закрывания затвора

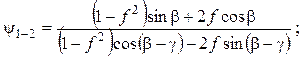
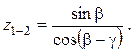
Библиографический список

1.  Проектирование спецмашин. ЧI. Проектирование стрелково-пушечного вооружения. Под ред. М.В. Грязева. Издательство ТулГУ. Тула. 2008г. 315с.

2.  Захаренков В.Ф. Внутренняя баллистика и автоматизация проектирования артиллерийский орудий. Санкт-Петербург. 2010. 276с.