Математическая модель функционирования артиллерийских автоматов с отводом пороховых газов

О.Г. Агошков, С.И. Кудрявцев, Д.Ю. Ульданов

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФУНКЦИОНИРОВАНИЯ АРТИЛЛЕРИЙСКИХ АВТОМАТОВ С ОТВОДОМ ПОРОХОВЫХ ГАЗОВ

Артиллерийские автоматы с газоотводной автоматикой нашли широкое применение в стрелково-пушечном вооружении, являясь автоматами второго класса, использующих энергию выстрела для осуществления процессов перезаряжания. Опыт проектирования таких автоматов дает многочисленные примеры рациональных подходов к разработки математических моделей функционирования их отдельных устройств и механизмов при использовании принципа декомпозиции указанных сложных технических систем. А математические модели, учитывающая в полной мере взаимное влияние этих устройств и механизмов на этапе эскизного проектирования автоматов применяются реже.

В настоящей статье рассматривается математическая модель функционирования механизмов автоматики на примере 23-мм автоматической авиационной пушки АМ-23 и 23-мм зенитного автомата 2А7, учитывающая взаимное влияние процессов происходящих в канале ствола и камере газового двигателя. В этих автоматах используется схема с ударным ускорительным механизмом досылания патрона. Схема автомата АМ-23 представлена на рис.1.

На основе построения математической модели функционирования артиллерийского автомата с газоотводной автоматикой лежит дифференциальное уравнение движения затворной рамы, принятой в качестве основного звена автоматического оружия 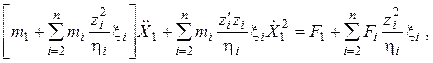(1).

                               (1)

где       – масса или момент инерции основного звена механизмов автоматического оружия;

 – масса или момент инерции i –го звена механизмов автоматики;

 – текущая координата основного звена;

- текущая координата i-го звена;

–сумма проекций сил на направление движения 1-го и i-го звена или сумма моментов относительно оси вращения всех сил, действующих на звено, совершающее движение;

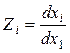 – передаточное отношение от звена, совершающего i-е движение, к основному;

 – коэффициент полезного действия механизма, представляющего собой отношение элементарной работы, передаваемой ведомому i-му звену, к элементарной работе, совершаемой ведущим звеном.

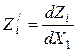 – изменение передаточного отношения i-го звена по координате движения основного звена;

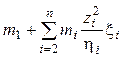= – приведенная масса;

 – коэффициент приведения масс;

 – коэффициент включения/выключения i-го звена в работу автоматики;

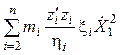 - приведенная к основному звену суммарная сила инерции звеньев механизма, обусловленная изменением передаточного отношения;

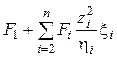 - приведенная к основному звену сумма всех внешних сил (или моментов);

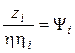 - коэффициент приведения сил, или коэффициент передачи сил от i-го звена к основному.

В основу уравнения (1) лежат следующие допущения:

-  звенья механизмов автоматики – абсолютно твердые тела;

-  зазоры и натяги в кинематических парах отсутствуют;

-  контакт между деталями механизмов точечный.

В рамках настоящей статьи рассматриваются схемы сил, действующих на звенья механизмов автоматики и коэффициенты приведения сил на характерных участках движения затворной рамы при ее движении назад – при открывании затвора, страгивании гильзы в начале ее экстракции и во втором этапе экстракции гильзы при работе ускорительного механизма, при работе механизма подачи.

В качестве математической модели функционирования газоотводного двигателя в отрасли нашла применение модель (руководящие технические материалы [РТМ В-3-71-70]), основанная на системе уравнений, основным из которых является уравнение скорости  изменения внутренней энергии порохового газа в газовой камере [2]

, где  - площадь сечения газового цилиндра;

- удельный приход энергии;

- удельный расход энергии;

 - секундный приход порохового газа через газопровод из канала ствола;

 - секундный расход порохового газа из камеры через газопровод в стол;

 - секундный расход порохового газа из камеры через зазор между цилиндром и поршнем;

 - механический эквивалент тепла;

теплоотдача от газа стенкам камеры

Система уравнений в [РТМ В-3-71-70] составлена при следующих допущениях:

-  рабочий процесс в газовой камере не влияет на рабочий процесс, протекающий в канале ствола;

-  течение газа в газопроводе и в зазоре между поршнем и цилиндром считается квазиустановившимся;

-  кинетическая энергия порохового газа в камере мала по сравнению с внутренней энергией газа;

-  отношение теплоемкостей порохового газа принимается постоянным.

Математическая модель баллистического расчета артиллерийских установок, в том числе с отводом пороховых газов из канала с учетом взаимодействия с газовым буфером. В настоящее время реализованы в новом методе построения математических моделей для отдельных конструктивных элементов ив комплексе прикладных программ, разработанных профессором д.т.н. В.Ф. Захаренковым в БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова.

Синтез из этих конструктивных элементов конкретных баллистических схем установок позволяет получить комплексные математические модели, но без учета работы механизмов автоматики.

Математическая модель данного автомата включает в себя: пороховую камору, ствол со снарядом, газовую камеру, отверстие, зазор между поршнем и цилиндром газовой камеры, газоотводный канал газового буфера, газовую камеру газового буфера (при его заполнении газом).

Таким образом, разработка данной модели и программного комплекса позволяют во многом учесть взаимное влияние газодинамических процессов, происходящих в канале ствола, газовом двигателе, газовом буфере при создании новых технических решений баллистических установок (в том числе и артиллерийских автоматов с отводом пороховых газов из канала ствола).

Не решенной проблемой в отрасли остается автоматизация синтеза математических моделей, отражающих работу механизмов автоматики и построение на этой базе программного комплекса.

Специфика математических моделей функционирования механизмов автоматики состоит в их  прерывистом характере, обусловленном изменением структуры ведомых звеньев, передаточных чисел, передаточных отношений сил и изменением приведенной массы ведущего звена.