Решение обыкновенных дифференциальных уравнений методом Эйлера и конечно-разностным методом

БГТУ «Военмех» им. Д.Ф. Устинова

Кафедра космических летательных аппаратов и разгонных блоков

Лабораторная работа №2

Решение обыкновенных дифференциальных уравнений

Подготовил студент группы М171

Бокучава П.Н.

Проверил доц. Ходосов В.В.

СПб,

2010

Решение обыкновенных дифференциальных уравнений

Вариант 1

Задание:

1.  Записать ОДУ в форме Коши

2.  Методом Эйлера и конечно-разностным методом получить решение ОДУ

3.  Решить ОДУ средствами MATLAB

4.  Определить ошибку в каждой точке.

Условия:

ОДУ:

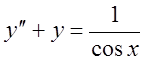
Начальные условия:

Отрезок интегрирования:

Точное решение:

Граничные условия:

1.  Форма Коши

Записанное в форме Коши, уравнение будет иметь вид:

2.1. Решение задачи Коши  методом Эйлера

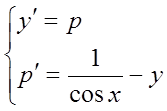
Разобьем отрезок интегрирования на четыре части, с шагом h=0.125:

Воспользуемся методом Эйлера:

Определим погрешность в каждой точке, сравнив ответ с точным решением:

2.2. Решение краевой задачи конечно-разностным методом

Разобьем отрезок интегрирования на четыре части, с шагом h=0.125:

Составим уравнения для граничных точек: для левой точки

,

и для правой точки

  заменим на левое разностное отношение

,

Составим уравнения для средних точек, заменив в ДУ производные разностными формулами:

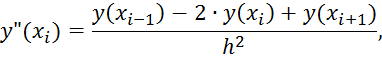
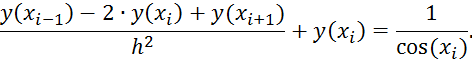
Упростим выражение

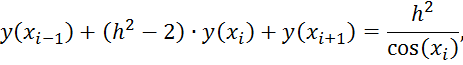
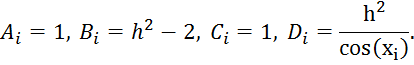
Запишем систему уравнений  в матричном виде:

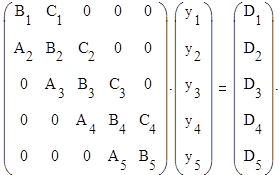
Решим эту систему методом прогонки. Найдем прогоночные коэффициенты и посчитаем значение функции в конце отрезка.

На конце отрезка функция принимает значение:

3.  Решение ОДУ средствами MATLAB

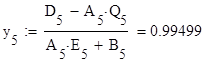
Воспользуемся программой Simulink, встроенной в MATLAB. Для определения искомого значения функции создадим схему, описывающую решение ДУ и определение погрешностей.

Схема решения:

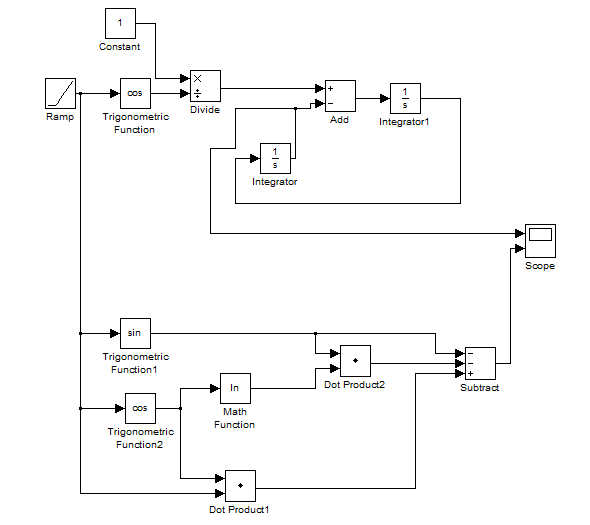
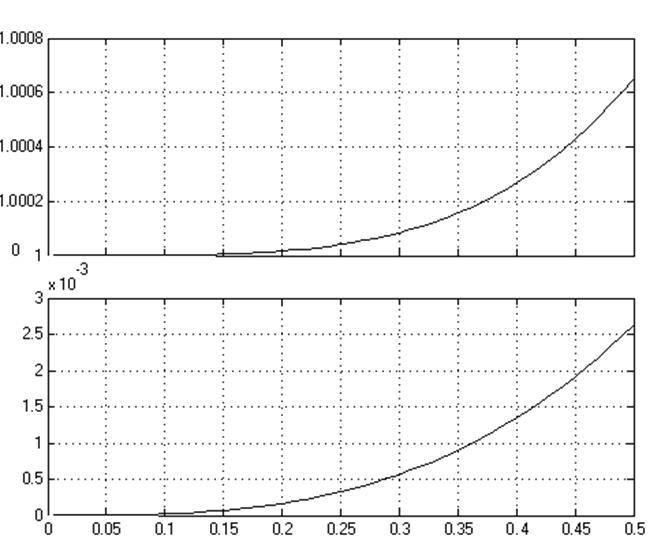
Подставив начальные условия в блоки интегрирования и задав длину отрезка интегрирования, получим графики значений функции и абсолютной погрешности вычислений.

График результатов вычислений по схеме(верхний – значение функции, нижний – абсолютная погрешность):