В этом уравнении ускорение точки А известно и по
модулю, и по направлению, ускорение 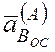 всегда направлено к
полюсу А и по модулю равно
всегда направлено к
полюсу А и по модулю равно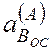 =
= ![]() =0,232p2 = 0,053p2
м/с2, ускорение
=0,232p2 = 0,053p2
м/с2, ускорение 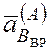
направлено перпендикулярно АВ и по модулю равно 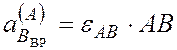 ¾
не известно, ускорение точки В не известно ни по модулю, ни по направлению.
Уравнение (1) с двумя неизвестными не решается.
¾
не известно, ускорение точки В не известно ни по модулю, ни по направлению.
Уравнение (1) с двумя неизвестными не решается.
Но точка В принадлежит звену ВО1Е , совершающего вращательное движение вокруг точки О1, и движется по окружности с центром О1, так что ее ускорение имеет две составляющие:
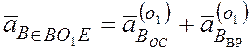 .
(2)
.
(2)
В уравнении (2) ускорение 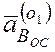 всегда
направлено к точке О1 , т.е. к оси вращения звена В О1Е
и по модулю равно
всегда
направлено к точке О1 , т.е. к оси вращения звена В О1Е
и по модулю равно 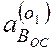 =
= ![]() =
=
=0,232p2
× 0,5= 0,026p2 м/с2, ускорение 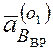 направлено перпендикулярно В О1
и по модулю равно
направлено перпендикулярно В О1
и по модулю равно 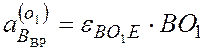 ¾ не известно, ускорение точки В не известно ни по
модулю, ни по направлению. Уравнение (2) с двумя неизвестными не решается.
¾ не известно, ускорение точки В не известно ни по
модулю, ни по направлению. Уравнение (2) с двумя неизвестными не решается.
Поскольку левые части уравнений (1) и (2) равны , то приравнивая правые части этих уравнений, получаем уравнение (3):
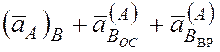 =
= 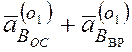 , (3)
, (3)
где ![]() м/с2 ,
м/с2 , 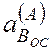 =
= ![]() =
0,053p2 м/с2,
=
0,053p2 м/с2,
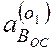 =
= ![]() =
0,026p2 м/с2,
=
0,026p2 м/с2, 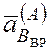 направлено перпендикулярно АВ и по
модулю равно
направлено перпендикулярно АВ и по
модулю равно 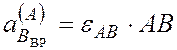 ¾
не известно,
¾
не известно,
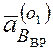 направлено
перпендикулярно ВО1 и по модулю равно
направлено
перпендикулярно ВО1 и по модулю равно 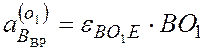 ¾
не известно.
¾
не известно.
Таким образом,
в уравнении (3) неизвестны только модули двух векторов 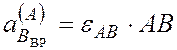 и
и
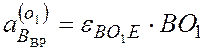 , и поэтому его можно решить. Решим это
уравнение аналитически, спроецировав его на оси
, и поэтому его можно решить. Решим это
уравнение аналитически, спроецировав его на оси
![]() , совпадающей с прямой ВО1,
и
, совпадающей с прямой ВО1,
и![]()
![]() , перпендикулярной к ВО1,
( предварительно изобразив на схеме векторы, входящие в это уравнение):
, перпендикулярной к ВО1,
( предварительно изобразив на схеме векторы, входящие в это уравнение): 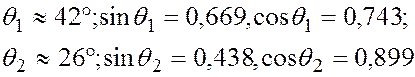 .
.
Проекция уравнения (3) на ось ![]() :
:
![]() ×сos
q1 -
×сos
q1 - 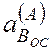 ×sin q2 -
×sin q2 -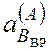 ×
cosq2
=
×
cosq2
= 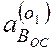 +0,
+0,
![]() × 0,743 - 0,053p2×0,438
-
× 0,743 - 0,053p2×0,438
- 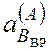 × 0,899 = 0.026p2 , откуда находим
× 0,899 = 0.026p2 , откуда находим 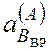 =
= 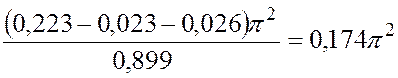 м/с2 > 0, и угловое ускорение
м/с2 > 0, и угловое ускорение 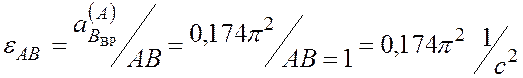 .
.
Направление углового ускорения находим по направлению
вектора 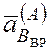 , т.е.
, т.е. ![]() , т.е.
против хода часовой стрелки, и показываем на схеме.
, т.е.
против хода часовой стрелки, и показываем на схеме.
Проекция уравнения (3) на ось ![]() , перпендикулярную к ВО1:
, перпендикулярную к ВО1:
-![]() ×sin q1
+
×sin q1
+ 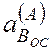 ×cos q2
-
×cos q2
-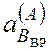 × sinq2 = 0 -
× sinq2 = 0 - 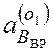 ,
,
-![]() ×
0,669 + 0,053p2×0,899 - 0,174p2× 0,438 = -
×
0,669 + 0,053p2×0,899 - 0,174p2× 0,438 = -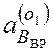 , откуда находим
, откуда находим 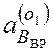 =
= ![]() м/с2 > 0, и угловое ускорение
м/с2 > 0, и угловое ускорение 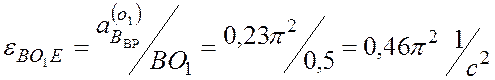 .
.
Направление углового ускорения находим по направлению вектора
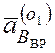 , т.е.
, т.е. ![]() ,
т.е. по ходу часовой стрелки, и показываем на схеме .
,
т.е. по ходу часовой стрелки, и показываем на схеме .
Ускорение точки В :
![]() =
= ![]() м/с2.
м/с2.
3) ─Ускорение точки Е:
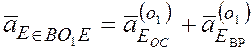 ,
,
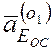 всегда направлено к точке О1
, т.е. к оси вращения звена ВО1Е и по модулю равно
всегда направлено к точке О1
, т.е. к оси вращения звена ВО1Е и по модулю равно 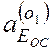 =
= ![]() = 0,232p2 ×
0,4= 0,021p2 м/с2,
= 0,232p2 ×
0,4= 0,021p2 м/с2,
ускорение 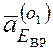 направлено
перпендикулярно ЕО1 в сторону
направлено
перпендикулярно ЕО1 в сторону ![]()
и по модулю равно 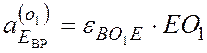 =
=![]() м/с2.
м/с2.
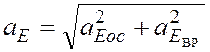 =
= ![]() м/с2.
м/с2.
4) ─ Ускорение точки F:
Ускорение точки F , принадлежащей шатуну EF, совершающего плоскопараллельное движение, определяется аналитически методом полюса. Приняв за полюс точку E, ускорение которой найдено, имеем
![]() (4)
(4)
или с учетом того, что 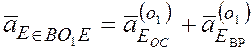 ,
получаем
,
получаем
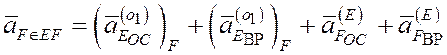 . (5)
. (5)
В этом уравнении составляющие ускорения точки E известны и по модулю, и по направлению, ускорение ![]() всегда направлено к полюсу E и по модулю равно
всегда направлено к полюсу E и по модулю равно![]() =
= ![]() =0,0632p2 1,2 = 0,005p2 м/с2, ускорение
=0,0632p2 1,2 = 0,005p2 м/с2, ускорение ![]() направлено перпендикулярно EFи по модулю равно
направлено перпендикулярно EFи по модулю равно ![]() ¾ не известно, вектор ускорение точки F ─
¾ не известно, вектор ускорение точки F ─ ![]() не известен
по модулю, но линия действия его известна ─ параллельна оси Oy─
вертикаль OF.
не известен
по модулю, но линия действия его известна ─ параллельна оси Oy─
вертикаль OF.
Таким образом,
в уравнении (5) неизвестны только модули двух векторов ![]() и
и
![]() , и поэтому его можно решить аналитически,
спроецировав это уравнение на оси x,
совпадающей с прямой EF, и h, перпендикулярную к EF,
( предварительно изобразив на схеме векторы, входящие в это уравнение):
, и поэтому его можно решить аналитически,
спроецировав это уравнение на оси x,
совпадающей с прямой EF, и h, перпендикулярную к EF,
( предварительно изобразив на схеме векторы, входящие в это уравнение):
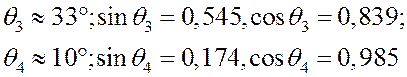 .
.![]()
Проекция уравнения (5) на ось x,
перпендикулярную неизвестному вектору![]() :
:
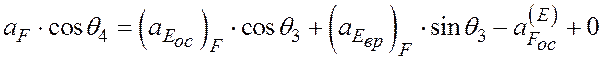
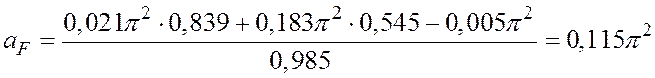 м/с2 > 0.
м/с2 > 0.
Спроецировав уравнение (5) на ось h, перпендикулярную шатуну EF, имеем
![]()
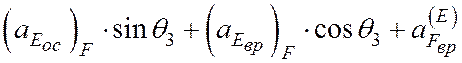 ,
,
![]()
откуда находим
![]()
![]() >
0 . Если
>
0 . Если 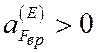 , то направление вектора
, то направление вектора ![]() выбрано правильно и
выбрано правильно и 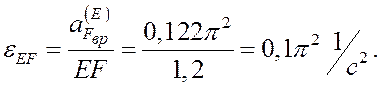
Направление углового ускорения ![]() находим
по направлению вектора
находим
по направлению вектора
![]() , т.е.
, т.е. ![]() ,
т.е. по ходу часовой стрелки, и показываем на схеме .
,
т.е. по ходу часовой стрелки, и показываем на схеме .
О т в е т: ![]() =p
с-1;
=p
с-1; ![]() =0,23p с-1;
=0,23p с-1;![]() =0,23p с-1;
=0,23p с-1; ![]() =0,063p
с-1;
=0,063p
с-1;
![]() = 0,3p
= 0,3p ![]() ;
; ![]() =0,115p
=0,115p ![]() ;
;
![]() = 0,092p
= 0,092p
![]() ;
;![]() = 0,044p
= 0,044p
![]() .
.
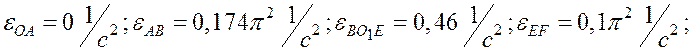
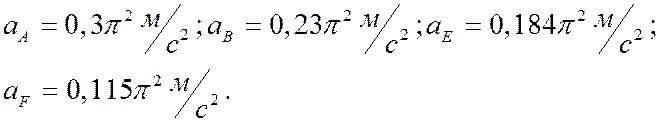
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.