





Работа силы.
Для того, чтобы рассмотреть теорему об изменении кинетической энергии, необходимо ввести новое понятие для силы – работу силы. Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.
Пусть на материальное тело действует сила ![]() .
Элементарная работа силы
.
Элементарная работа силы ![]() определяется выражением:
определяется выражением:
![]() , (1)
, (1)
где ![]() - алгебраическая величина проекции силы на
касательную в данной точке траектории, G – траекторная
координата.
- алгебраическая величина проекции силы на
касательную в данной точке траектории, G – траекторная
координата.
Но ![]() , где
, где 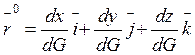 - орт
касательной, так как из кинематики точки известно, что
- орт
касательной, так как из кинематики точки известно, что 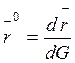 ,
а
,
а ![]() , где
, где ![]() -
радиус-вектор.
-
радиус-вектор.
Сила ![]() в проекциях на оси декартовой системы
координат 0xyz:
в проекциях на оси декартовой системы
координат 0xyz:
![]() , то есть
, то есть
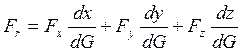
Элементарная работа силы 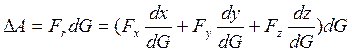 окончательно
определяется равенством:
окончательно
определяется равенством:
![]() (2)
(2)
Так как ![]() , где
, где ![]() - радиус-вектор точки, то (2) может быть записано
в форме скалярного произведения:
- радиус-вектор точки, то (2) может быть записано
в форме скалярного произведения:
![]() (3)
(3)
Так как 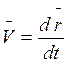 , то
, то
![]() (4)
(4)
Элементарная работа силы может иметь еще одно выражение. Известно, что
путь S, пройденный материальной точкой, величина
существенно положительная и возрастающая, то есть ![]() , где G – траекторная координата (знак «+» - движение материальной
точки в сторону положительных траекторных координат, рис. А, знак «-» - в
сторону отрицательных, рис. Б).
, где G – траекторная координата (знак «+» - движение материальной
точки в сторону положительных траекторных координат, рис. А, знак «-» - в
сторону отрицательных, рис. Б).
Из рисунков видно, что ![]() (знак «+» - движение
материальной точки в сторону положительных траекторных координат, знак «-» - в
сторону отрицательных). То есть
(знак «+» - движение
материальной точки в сторону положительных траекторных координат, знак «-» - в
сторону отрицательных). То есть
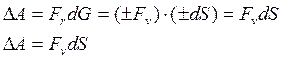 (5)
(5)
Для определения полной работы силы ![]() на
перемещении от
на
перемещении от ![]() до
до ![]() нужно
просуммировать элементарные работы на элементарных перемещениях. В пределе из
(1) получаем криволинейный интеграл.
нужно
просуммировать элементарные работы на элементарных перемещениях. В пределе из
(1) получаем криволинейный интеграл.
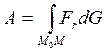 (6)
(6)
Из (6)-(10) следует, что работа силы – скалярная (положительная или отрицательная) физическая величина, характеризующая действие этой силы на некотором конечном перемещении материальной точки. Аналогично:
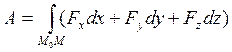 (7)
(7)
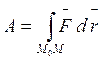 (8)
(8)
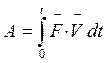 (9)
(9)
- в этом случае криволинейный ![]() сводится к обычному
определенному
сводится к обычному
определенному ![]() .
.
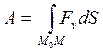 (10)
(10)
Из (10) следует, что если сила, действующая на материальную точку, перпендикулярна скорости этой точки во все время движения, то работа этой силы равна 0. Например, при движении материальной точки по горизонтальной плоскости работа силы тяжести этой точки равна 0.
Если сила приложена к точке, скорость которой равна 0, то работа этой силы также равна 0. Примером может служить работа силы трения скольжения, действующей на колесо, катящееся без скольжения по рельсу (точка касания колеса с рельсом – м.ц.е. колеса).
Пусть на материальную точку действует система сил ![]() .
Из определения элементарной и полной работы следует: работа равнодействующей
системы сил, действующих на материальную точку, на данном перемещении ее равна
сумме работ всех сил данной системы на том же перемещении.
.
Из определения элементарной и полной работы следует: работа равнодействующей
системы сил, действующих на материальную точку, на данном перемещении ее равна
сумме работ всех сил данной системы на том же перемещении.
![]() , где
, где ![]() - работа равнодействующей системы сил,
- работа равнодействующей системы сил, ![]() - работа силы
- работа силы ![]() данной
системы сил.
данной
системы сил.
Теорема об изменении кинетической энергии материальной точки.
Пусть материальная точка М массы m движется под действием системы сил (![]() )
относительно некоторой системы отсчета по заданной траектории. В начальный
момент времени точка занимала положение
)
относительно некоторой системы отсчета по заданной траектории. В начальный
момент времени точка занимала положение ![]() и имела
в этот момент времени скорость
и имела
в этот момент времени скорость ![]() . Под действием заданной
системы сил материальная точка переместилась в положение М, при этом скорость
ее стала равной
. Под действием заданной
системы сил материальная точка переместилась в положение М, при этом скорость
ее стала равной ![]() .
.
Найдем связь между работой сил, приложенных к материальной точке, и изменением скорости точки. Для этого воспользуемся основным уравнением динамики
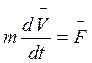 , где
, где ![]() - равнодействующая всех сил, приложенных к
материальной точке. Умножим обе части его скалярно на дифференциал
радиуса-вектора
- равнодействующая всех сил, приложенных к
материальной точке. Умножим обе части его скалярно на дифференциал
радиуса-вектора ![]() .
.
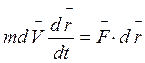
![]()
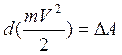 (*)
(*)
Половина произведения массы точки на квадрат ее скорости называется кинетической энергией материальной точки:
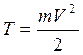
Кинетическая энергия материальной точки – скалярная положительная физическая величина, характеризующая динамическое состояние этой материальной точки в данный момент времени.
(*) – теорема об изменение кинетической энергии материальной точки в дифференциальной форме: полный дифференциал кинетической энергии материальной точки равен элементарной работе всех действующих на эту точку сил.
Проинтегрируем обе части (*) по кривой ![]() ,
получим теорему об изменении кинетической энергии в конечной форме:
,
получим теорему об изменении кинетической энергии в конечной форме:
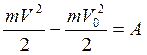 (**)
(**)
Изменение кинетической энергии материальной точки при переходе ее из начального в конечное положение равно сумме работ на этом перемещении всех сил, приложенных к точке.
С помощью этой теоремы можно решать две задачи:
- Определять скорость материальной точки в конце или начале движения. (**) применяют, если работу можно вычислить, не зная закона движения.
- Вычисление работы силы по заданной скорости. (**) применяют, когда неизвестна аналитическая зависимость силы или трудно определить закон движения.
Частные случаи вычисления работы силы.
1. Работа центральной силы. Центральная сила – силы, линия действия которой во все время движения проходит через неподвижный центр (центр силы), а величина зависит от расстояния материальной точки до этого центра. Центральные силы могут быть силами притяжения (рис. А) или силами отталкивания (рис. Б).
![]() , где
, где ![]()
(«+» - сила отталкивания, «-» - притяжения), r – длина
радиуса-вектора, ![]() - его орт.
- его орт.
Работа силы при перемещении материальной точки из ![]() в
M:
в
M:
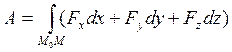
Найдем алгебраические величины проекций силы ![]() на оси
на оси ![]() .
.
Орт: 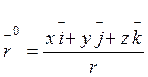
Центральная сила: 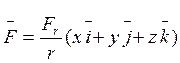
То есть: 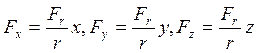
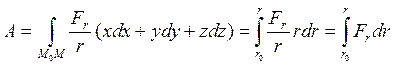 ,
,
так как ![]() , то
, то ![]()
Окончательно:
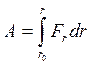
- работа центральной силы, переменной по величине и направлению, не зависит от формы траектории, по которой движется точка (а, значит, от длины пути, пройденного ею). А зависит только от начального и конечного положения.
Пример центральной силы – сила упругости пружины, величина которой прямопропорциональна ее удлинению, а линия действия проходит через неподвижную (.) О.
![]() - длина пружины в недеформированном
состоянии. Сила упругости
- длина пружины в недеформированном
состоянии. Сила упругости ![]() , где c
– коэффициент жесткости.
, где c
– коэффициент жесткости.
![]()
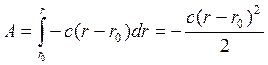 ,
,
![]() - удлинение пружины.
- удлинение пружины.
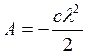
2. Работа постоянной по величине силы сопротивления. Сила
сопротивления, действующая на материальную точку, направлена в сторону,
противоположную скорости этой точки, то есть ![]() , где F=Const.
, где F=Const.
Работу этой силы при перемещении материальной точки из положения ![]() в положение M определим по формуле (10). Отсчет начала пути будет
совпадать с
в положение M определим по формуле (10). Отсчет начала пути будет
совпадать с ![]() , а
, а ![]()
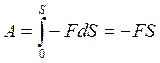 , то есть работа постоянной по величине силы сопротивления будет зависеть
от длины пути, пройденного материальной точкой при перемещении ее из
, то есть работа постоянной по величине силы сопротивления будет зависеть
от длины пути, пройденного материальной точкой при перемещении ее из ![]() в M.
в M.
3. Работа постоянной силы. Пусть на материальную точку действует
постоянная сила ![]() . Вычислим
работу этой силы на некотором перемещении точки из состояния
. Вычислим
работу этой силы на некотором перемещении точки из состояния ![]() в
в ![]() ,
, ![]()
![]() .
.
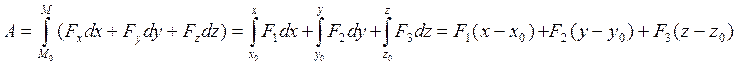
- работа постоянной силы не зависит от формы траектории или от длины пути, пройденного точкой, а зависит лишь от начального и конечного положения точки на траектории.
Примером постоянной силы может служить сила тяжести. Вблизи поверхности Земли она равна по величине mg и направлена по вертикали вниз.
В системе координат с осью Z, направленной
вертикально вверх, и плоскостью x0y горизонтальной, составляющие силы тяжести![]() и работа силы при перемещении точки из
положения
и работа силы при перемещении точки из
положения ![]() в положение
в положение ![]() -
-
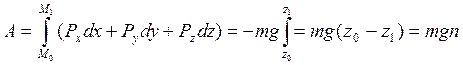
Работа будет положительной, если материальная точка движется вниз, и отрицательной при ее движении вверх.
По виду производимой ими работы силы можно разделить на два класса. Консервативными называются силы, работа которых не зависит ни от формы траектории, ни от пути, проходимого точкой приложения силы, а зависит от начального и конечного положения этой точки. Силы, неудовлетворяющие этому условию, называются неконсервативными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.