ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ![]()
Кафедра “Теоретические основы электротехники”
Лабораторная работа № 35
“Исследование одноконтурной цепи при периодических несинусоидальных напряжении и токе”
Выполнил:
студент группы ЭТ-401
Кожевников Д. М.
Санкт-Петербург
2006
ВВЕДЕНИЕ
Цель работы- экспериментальное
исследование влияния параметров ![]() ,
, ![]() ,
, ![]() на форму кривой
тока; исследование явления резонанса в одноконтурной электрической цепи при
несинусоидальном напряжении питания.
на форму кривой
тока; исследование явления резонанса в одноконтурной электрической цепи при
несинусоидальном напряжении питания.
ПРОГРАММА РАБОТЫ
1. Экспериментальная часть.
1.1. Экспериментальное исследование влияния параметров цепи на форму кривой тока при несинусоидальном напряжении на зажимах цепи.
1.2. Исследование
резонанса напряжений при несинусоидальной форме напряжений тока цепи (получение
резонансов для первой и третьей гармоник путем изменения параметра ![]() ).
).
2. Обработка экспериментальных данных. Расчеты.
2.1. Разложение несинусоидальной кривой напряжения в ряд Фурье. Графическая проверка результатов разложения.
2.2. Аналитический
расчет несинусоидальных токов в реальной катушке и в цепи с последовательным
соединением ![]() ,
, ![]() ,
, ![]() (в последнем случае – при резонансах для
первой и третей гармоник).
(в последнем случае – при резонансах для
первой и третей гармоник).
2.3. Сопоставление кривой одного из рассчитанных токов с экспериментальной кривой.
Таблица 1
Характеристика измерительных приборов
|
Наименование и тип прибора |
Система прибора |
Класс точности |
Заводской номер |
Предел измерений |
Цена деления |
|
Вольтметр |
МЭ |
0,5 |
77789 |
30 В |
0,2 В |
|
Амперметр |
МЭ |
0,5 |
81370 |
200 мА |
2 мА |
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Во многих случаях периодические э.д.с., токи и напряжения несинусоидальны и могут быть представлены в виде гармонического ряда Фурье. Как известно, ряд Фурье в общем случае содержит постоянную составляющую, основную (первую) гармонику, имеющую период, равный периоду э.д.с. (напряжения, тока) и высшие гармоники, частоты в целое число раз больше частоты первой гармоники. Например,
![]() .
.
В общем случае ряд Фурье содержит бесконечное число членов, но обычно на практике можно ограничиться некоторым конечным числом членов.
Для вычисления коэффициентов ряда (![]() ;
; ![]() и т.д.) целесообразно его члены выразить через синусы и
косинусы без начальных фаз:
и т.д.) целесообразно его члены выразить через синусы и
косинусы без начальных фаз:
![]() ,
,
и, следовательно,
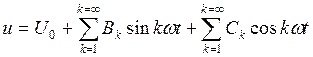 .
.
В таком
случае постоянная составляющая и коэффициенты ![]() и
и
![]() могут быть
определены по формулам, известным из математики:
могут быть
определены по формулам, известным из математики:
|
|
(1) |
Имея ![]() и
и ![]() , нетрудно
вычислить амплитуду и начальную фазу
, нетрудно
вычислить амплитуду и начальную фазу ![]() - той гармоники:
- той гармоники:
![]() ;
; 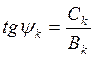 .
.
Следует помнить, что значение ![]() определяется через
определяется через ![]() неоднозначно. Угол уточняется сопоставлением знаков
неоднозначно. Угол уточняется сопоставлением знаков ![]() и
и 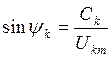 .
.
Приведенные формулы (1) могут быть использованы, когда
функция ![]() задана аналитически. В лабораторной работе
мы располагаем кривыми (осциллограммами) э.д.с., тока или напряжения. В подобных случаях пользуются приближенными методами
интегрирования. Например, можно воспользоваться приближенными формулами (2):
задана аналитически. В лабораторной работе
мы располагаем кривыми (осциллограммами) э.д.с., тока или напряжения. В подобных случаях пользуются приближенными методами
интегрирования. Например, можно воспользоваться приближенными формулами (2):
|
|
(2) |
Для использования формул (2) делят период ![]() на
на ![]() равных
интервалов и в
равных
интервалов и в ![]() точках определяют ординаты
точках определяют ординаты 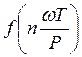 заданной графически кривой, полагая
заданной графически кривой, полагая ![]() =
1, 2, 3, …,
=
1, 2, 3, …, ![]() .
.
Разложение функции в гармонический ряд упрощается, если график ее обладает симметрией. В случае наиболее часто встречаемой на практике симметрии относительно оси абсцисс или так называемой зеркальной симметрии, т.е. при условии:
|
|
(3) |
постоянная составляющая и четные гармоники отсутствуют, а первая
половина слагаемых под знаком суммы в формулах (2) для ![]() и
и ![]() (для нечетных гармоник) равна
второй половине слагаемых. Ряд получает вид:
(для нечетных гармоник) равна
второй половине слагаемых. Ряд получает вид:
![]() .
.
В случае симметрии относительно начала координат, т.е. при
условии ![]() формулы
(2) для постоянной составляющей и для всех коэффициентов
формулы
(2) для постоянной составляющей и для всех коэффициентов ![]() дают нуль.
Ряд получает вид:
дают нуль.
Ряд получает вид:
![]() .
.
В случае последовательного соединения реальной индуктивной катушки
и конденсатора для ![]() - той
гармоники имеем:
- той
гармоники имеем:
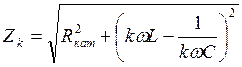 ;
; 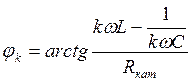 ,
,
где ![]() - активное
сопротивление реальной катушки.
- активное
сопротивление реальной катушки.
Мгновенное значение ![]() - той
гармоники тока:
- той
гармоники тока:
![]() ,
,
где 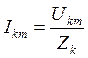 .
.
Постоянная составляющая тока в такой цепи равна нулю, так как конденсатор постоянный ток не проводит. Ток цепи:
![]() .
.
В последовательном соединении ![]() ,
, ![]() ,
, ![]() может наблюдаться случай, когда для
может наблюдаться случай, когда для ![]() - й гармоники индуктивное сопротивление равно емкостному. В таком случае действующее значение
- й гармоники индуктивное сопротивление равно емкостному. В таком случае действующее значение ![]() - й гармоники тока (4) возрастает:
- й гармоники тока (4) возрастает:
|
|
(4) |
Действующее значение несинусоидального тока (5) может
возрасти, так как ![]() - я гармоника в кривой тока проявляется
больше, чем в кривой напряжения:
- я гармоника в кривой тока проявляется
больше, чем в кривой напряжения:
|
|
(5) |
Из равенства
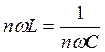
следует: сохраняя из двух величин (![]() и
и ![]() ) одну постоянной
и изменяя другую, можно обеспечить это равенство для различных значений
) одну постоянной
и изменяя другую, можно обеспечить это равенство для различных значений ![]() , т.е. получать резонанс для различных гармоник; графики зависимостей
, т.е. получать резонанс для различных гармоник; графики зависимостей ![]() и
и ![]() могут иметь несколько максимумов.
могут иметь несколько максимумов.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Экспериментальная часть
Работа выполняется по схеме на рис. 1.
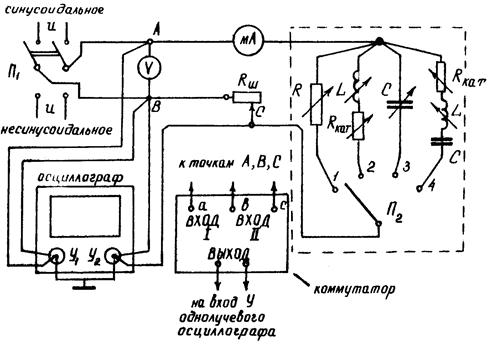
Рис. 1
1.1. Экспериментальное исследование влияния параметров цепи на форму кривой тока при несинусоидальном напряжении на зажимах цепи
Экспериментальное определение характерных особенностей
кривых тока в приемниках - резисторе, реальной катушке и конденсаторе - при
питании их от источника несинусоидального напряжения состоит в наблюдении и
снятии осциллограмм тока и напряжения (по одной для каждого приемника) с нанесенными
на осциллограммы осями абсцисс. Ось абсцисс можно получить, разорвав токовую
цепь переключателем ![]() .
.
Для последующего сопоставления осциллограмм с расчетными данными
на всех снимаемых в процессе работы осциллограммах должны быть указаны масштабы
кривых тока и напряжения, действующие значения тока и напряжения, а также величины ![]() ,
, ![]() ,
, ![]() . Масштаб напряжения обозначен на входном делителе
двухлучевого осциллографа. Масштаб тока получают делением амплитуды кривой
напряжения на шунте (кривой тока) на величину сопротивления шунта.
. Масштаб напряжения обозначен на входном делителе
двухлучевого осциллографа. Масштаб тока получают делением амплитуды кривой
напряжения на шунте (кривой тока) на величину сопротивления шунта.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.