Такое передаточное отношение можно обеспечить, применяя, например, планетарный механизм схемы «В». Произведём проектировочные расчёты.
Исходные данные для проектирования редуктора:
Требуемое передаточное отношение=5,84
Допустимая погрешность реализации=5%
Частота вращения выходного вала=125об/мин
Максимальный момент на выходном валу=190,674 Н*м
Ресурс работы передачи=5000час
Колёса: прямозубые
Термообработка: Zа – цементация Zg – нормализация или улучшение
Zf – цементация Zb– нормализация или улучшение
Сателлиты – сборные.
Число сателлитов=3
Коэффициенты ширины зубьев шестерён: Kza=1 Kzf=1
На рисунке 6.2 представлены результаты проектировочного расчёта.

Рис. 7.2
Исследование динамики работы машины и обеспечение требуемой плавности хода
8.1 Постановка задачи, уравнение движения
Исследуемый машинный агрегат совершает установившиеся движения. При этом период, через который повторяются все фазы технологического процесса, равен времени оборота кривошипа главного механизма.
Поскольку в данном случае число степеней свободы главного механизма W=1, то достаточно определить закон движения одного ведущего звена.
Таким образом, исследования предварительно можно сформулировать задачу математического моделирования движения главного вала машины под действием приложенных сил и моментов с помощью уравнения движения. Результатом, т.е. решение данного уравнения, будет искомый закон движения главного вала за один оборот.
Где φ – угол поворота главного вала, ω – его угловая скорость
По функции (8.1) можно установить максимальное ωmax и минимальное ωmin значение угловой скорости. По этим данным вычисляем коэффициент неравномерности хода.
Δ=2(ωmax- ωmin)/ (ωmax+ ωmin) (8.2), являющийся количественной характеристикой степени отклонения угловой скорости от среднего значения. По техническому заданию предельно допустимое значение коэффициента неравномерности хода [δ]=0.1, и проектируемой мошине должно выполняться условие:
Если в результате моделирования окажется, что условие δ <= [δ] не выполняется, то главный вал машины необходимо установить маховик, момент инерции которого должен быть подобран так, чтобы условие(8.3) выполнилось.
Резюмируя, можно окончательно сформулировать цели исследования как математическое моделирование движения главного вала машины и обеспечение на этой основе заданной плавности хода путем подбора требуемой маховой массы.
Математической моделью процесса является дифференциальное уравнение движения:
Jпр(φ)dω/dt + (ω2/2)·d Jпр/dω=MДпр – MСпр (8.4)
(ω2/2)d Jпр/dφ – момент обусловленный переменностью приведенного момента инерции.
Приведенный момент инерции в данном случае состоит из трех составляющих:
Jпр(φ) = Jгмпр(φ) + Jпрпр + Jммпр (8.5)
Приведенные моменты в правой части уравнения (8.4) являются функциями различных параметров. Исследуемая машина приводится в движение асинхронным электродвигателем, движущий момент которого MДпр = f(ω). Силы сопротивления обусловлены в первую очередь технологической операцией и до некоторой степени силами трения, так что MCПР=f(φ) – смотри раздел 5.
Решением уравнения (8.4) являются функции: ω(t)=φ(t). Исключая t как параметр получаем зависимость ω(φ).
8.2 Решение уравнения движения и подбор параметров маховика.
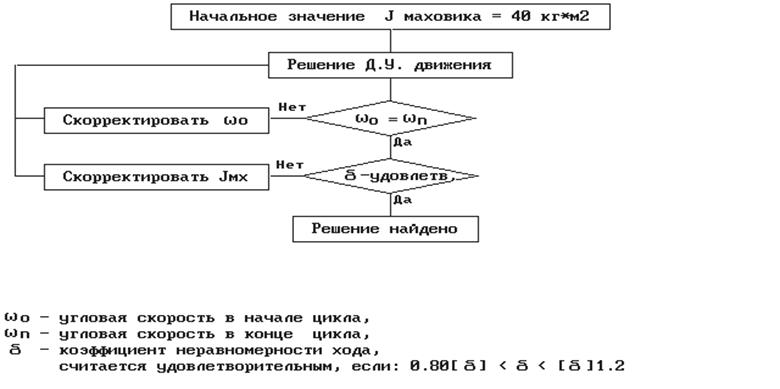
Для обеспечения требуемой плавности хода уравнение (8.4) решается. В процессе реализации варьируется значение момента инерции маховика JMX, входящее константой в JПР, и контролируется стационарность режима работы. Процесс идёт до тех пор, пока не будет найден вариант, удовлетворяющий заданному коэффициенту неравномерности хода.
Входные данные:
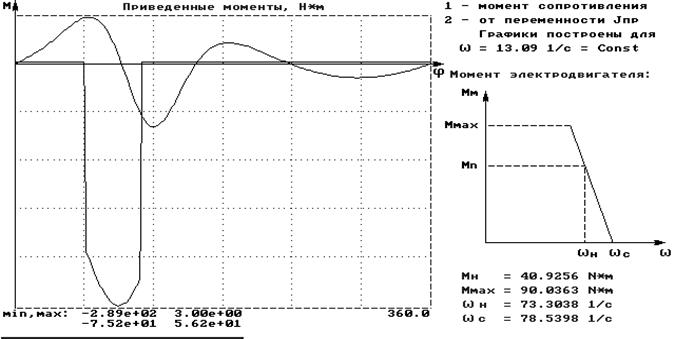
Полученные данные:
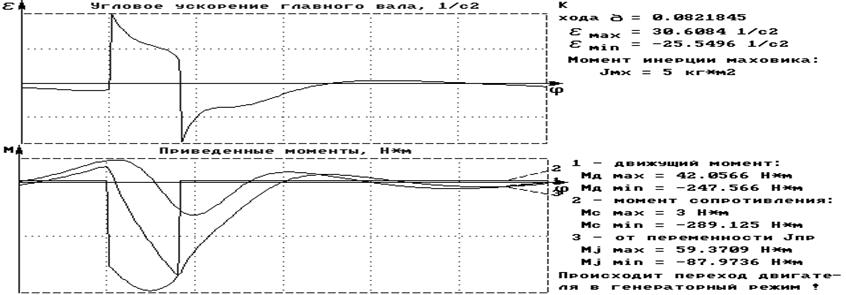
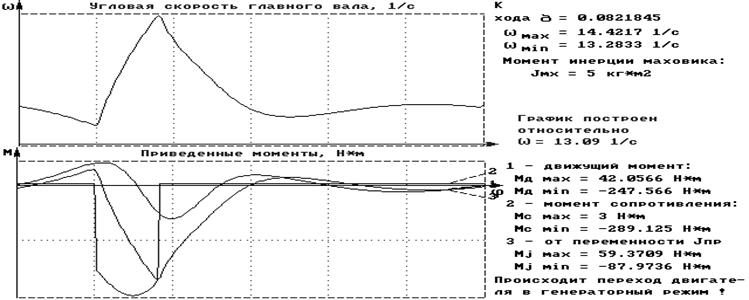
Анализ этих зависимостей показывает:
Рассчитаем ориентировочные размеры маховика. Для этого неоходимо приближённо предположить, что маховик представляет собой сплошной диск, момент инерции которого:
JMX= ρbπd4/32,
Где ρ – плотность материала ( для стали и чугуна можно принять ρ=7800 кг/м3); b,d – толщина и диаметр маховика, м.
Принимая для ориентировочного расчёта d/b=5, имеем:
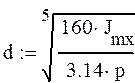
Конструктивно такой диаметр маховика слишком велик, однако маховики изготавливают так, чтобы основная масса располагалась ближе к ободу, в этом случае диаметр заметно уменьшается, кроме того и отношение d/b можно взять меньшим. Если устанавливать маховик не на главный вал, а на вал двигателя. То его момент инерции:
JMX = JMX/I2 = 14.98/13.232 = 0.085 кг*м2, где i – передаточное отношение зубчатого механизма.
В этом случае диаметр маховика:
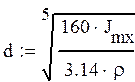
Заключение.
В данном курсовом проекте решены следующие задачи:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.