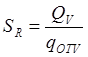Назначение, типы и состав системы обеспечения теплового режима. Работа газовой системы терморегулирования. Массовое уравнение. Расчет массовых и габаритных характеристик элементов, страница 4

                                                                 (5.13)

Масса радиатора , где =(3…15) кг/м² – удельная масса радиатора.

Площадь сечения газовода

, где                                             (5.14)

 - секундный расход, скорость и плотность газа соответственно.

Массовый секундный расход газа

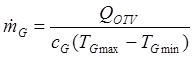 ,                                                      (5.15)

где  - отводимый тепловой поток равен внутреннему тепловому потоку гермоконтейнера;  - теплоемкость газа [Дж/(кг·К];  - максимальная (на входе в радиатор) и минимальная (на выходе из радиатора) температуры газа.

Скорость потока газа определяется по зависимости, составленной на основании критерия Рейнольдса.

Критерий Рейнольдса:         ,                                                              (5.16)

где  - определяющий размер и кинематическая вязкость газа [м²/с].

Определяющий размер:   ,                                                                                               (5.17)

где  - высота газовода.

С учетом (4.14 – 4.17) получим зависимость площади сечения газовода

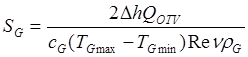                                             (5.18)

При расчете площади сечения газовода значение числа Рейнольдса выбирается из диапазона 2500…3000, что соответствует слабо турбулизированному режиму движения газа.

Примечание: Re≤2300 – ламинарный поток; Re≥10⁴ – турбулентный поток.

Для расчета площади и массы газовода необходимо знать размеры гермоотсека. Поскольку размеры гермоотсека определяются позже, масса газовода вначале определяется через массовый статистический коэффициент, зависящий от компоновки:

                                                                                    (5.19)

Масса регулятора ,                                                                                    (5.20)

где =(2…6) кг/кВт – удельная масса регулятора.

Масса вентилятора ,                                                                                  (5.21)

где =(0,8…2,6) кг/кВт.

Масса теплообменника газ-жидкость ,                                                      (5.22)

где =(4…6) кг/кВт.

Расчет массы газа ведется по уравнению Менделеева-Клапейрона

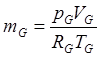,                                                                          (5.23)

где =1,3·10⁵Па – давление в гермоотсеке;  - объем газа; =8314/28 Дж/(кг·К) – газовая постоянная для азота; = (273+50)ºС - максимальная температура газа в гермоотсеке.

5.5. Уточненный расчет площади поверхности теплового радиатора

Для уточнения площади радиатора используется уравнение угла освещенности  плоскости орбиты (4.5). Угловыми коэффициентами    определяется доля падающего на поверхность КА собственного планетного излучения и доля отраженного от планеты солнечного излучения

              

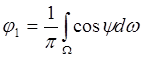
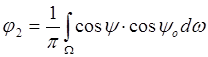
где  - угол, определяющий ориентацию локальной элементарной площадки поверхности;  - угол между направлениями Земля-КА и Земля-Солнце;  - телесный угол обзора планеты.

Расчетные соотношения для этих коэффициентов зависят от формы поверхности КА, его ориентации и в общем случае сложны. При сферической форме КА осредненные угловые коэффициенты находят по соотношениям

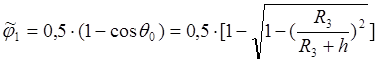
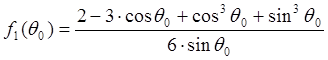
где  - угол между местной вертикалью и направлением, касательным к земной поверхности (угол  - является сечением телесного угла обзора планеты).

Плотность прямого собственного планетного излучения определяется уравнением:

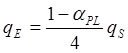                                                         (5.24)

Для случая термостатирования гермоконтейнера с целью учета его ориентации на орбите вводятся осредненные угловые коэффициенты, отнесенные к площади миделевого сечения радиационной поверхности

                  

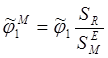
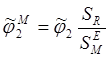
где  - площадь миделевого сечения радиационной поверхности по отношению к тепловому потоку.

Зависимость для плотности поглощенного теплового потока