Так как линейные (они же фазные) напряжения UAB, UBC, UCA симметричны, то и фазные токи образуют симметричную систему
İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.
Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°.
Линейные токи
İA = İab - İca; İB = İbc - İab; İC = İca - İbc;
образуют также симметричную систему токов (рис.3.13, 3.14).
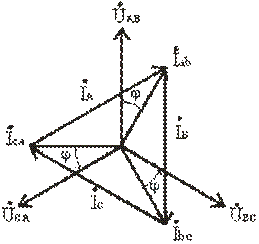
Рис. 3.13
На векторной диаграмме (рис. 3.14)
фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы
приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что
напряжение UAB имеет нулевую фазу. Из диаграммы следует, что любой
линейный ток больше фазного в 
раз. Линейный ток İA отстает по фазе от
фазного тока İab на угол 30°, на этот же угол отстает İB
от İbc, İC от İca.
Таким образом, при соединении
треугольником действующее значение линейного тока при симметричной нагрузке в раз больше действующего
значения фазного тока и UЛ = UФ; IЛ =IФ.
При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы.
Фазное напряжение UФ = UЛ.
Фазный ток IФ = UФ / ZФ,
линейный ток IЛ =IФ, угол сдвига по фазе
φ = arctg (XФ / RФ).
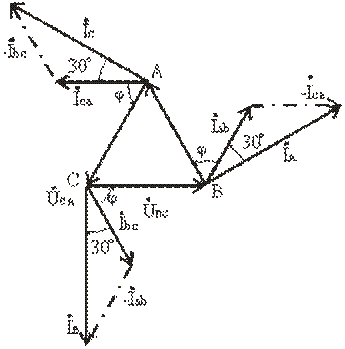
Рис. 3.14
В общем случае при несимметричной нагрузке Zab ≠ Zbc ≠ Zca. Обычно она возникает при питании от трехфазной сети однофазных приемников. Например, для нагрузки, рис. 3.15, фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными.
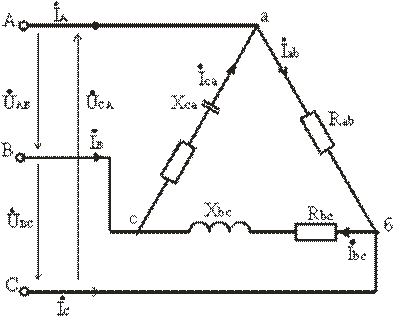
Рис. 3.15
Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активно-емкостная приведена на рис. 3.16, топографическая диаграмма – на рис. 3.17.
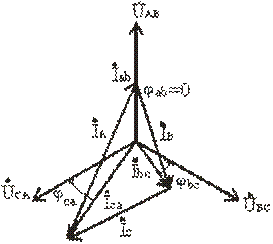
Рис. 3.16
Построение векторов линейных токов произведено в соответствии с выражениями
İA = İab - İca; İB = İbc - İab; İC = İca - İbc.
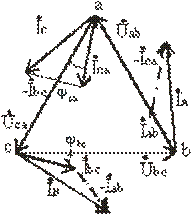
Рис. 3.17
Таким образом, при несимметричной нагрузке симметрия фазных токов İab, İbс, İca нарушается, поэтому линейные токи İA, İB, İC можно определить только расчетом по вышеприведенным уравнениям (3.20) или найти графическим путем из векторных диаграмм (рис. 3.16, 3.17).
Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки.
При расчете для несимметричной нагрузки сначала определяют значения фазных токов İab, İbc, İca и соответствующие им сдвиги фаз φab, φbc, φca. Затем определяют линейные токи с помощью уравнений (3.20) в комплексной форме или с помощью векторных диаграмм (рис. 3.16, 3.17).
1. При расчете трехфазных цепей исходят из предположения, что генератор дает симметричную систему напряжений. На практике несимметрия нагрузки практически не влияет на систему напряжений генератора в том случае, если мощность нагрузки мала по сравнению с мощностью генератора или сети электроснабжения.
2. Схема соединения обмоток трехфазного генератора не предопределяет схему соединения нагрузки. Так, при соединении фаз генератора в звезду нагрузка может быть соединена в звезду с нейтральным проводом, в звезду без нейтрального провода или, наконец, в треугольник.
В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей.
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз
(3.23)
P = Pa + Pb + Pc, где
(3.24)
Pa = Ua Ia cos φa; Pb = Ub Ib cos φb; Pc = Uc Ic cos φc; Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токи; φa, φb, φc – углы сдвига фаз между напряжением и током.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.