Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что
(3.15)
Úa = ÚA - ÚnN; Úb = ÚB - ÚnN; Úc = ÚC - ÚnN.
Зная фазные напряжения приемника, можно определить фазные токи:
(3.16)
İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc.
Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и UnN (рис. 3.11).
При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали UnN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно.
Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).
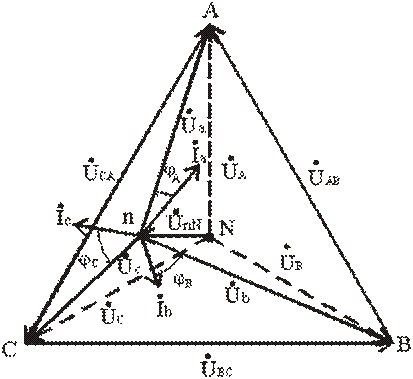
Рис. 3.11
Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.
Поэтому нейтральный провод необходим для того, чтобы:
Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.
При соединении источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началом В второй фазы, конец Y второй фазы – с началом С третьей фазы, конец третьей фазы Z – c началом первой фазы А. Начала А, В и С фаз подключаются с помощью трех проводов к приемникам.
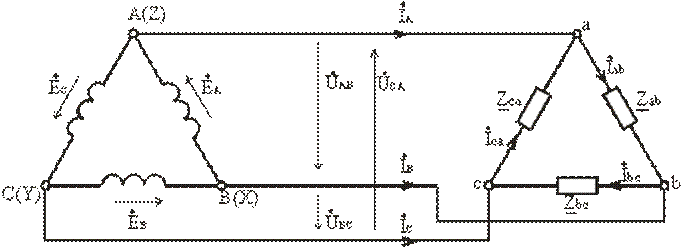
Рис. 3.12
Соединение фаз источника в замкнутый треугольник возможно при симметричной системе ЭДС, так как
(3.17)
ĖA + ĖB + ĖC = 0.
Если соединение обмоток треугольником выполнено неправильно, т.е. в одну точку соединены концы или начала двух фаз, то суммарная ЭДС в контуре треугольника отличается от нуля и по обмоткам протекает большой ток. Это аварийный режим для источников питания, и поэтому недопустим.
Напряжение между концом и началом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению.
(3.18)
UЛ = UФ.
Пренебрегая сопротивлением линейных проводов, линейные напряжения потребителя можно приравнять линейным напряжениям источника питания: Uab = UAB, Ubc = UBC, Uca = UCA. По фазам Zab, Zbc, Zca приемника протекают фазные токи İab, İbc и İca. Условное положительное направление фазных напряжений Úab, Úbc и Úca совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов İA, İB и İC принято от источников питания к приемнику.
В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Токи в фазах приемника определяются по формулам
(3.19)
İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.
Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c (рис 3.12)
(3.20)
İA = İab - İca; İB = İbc - İab; İC = İca - İbc.
Сложив левые и правые части системы уравнений, (3.20), получим
(3.21)
İA + İB + İC = 0, т.е. сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке.
При симметричной нагрузке
(3.22)
Zab = Zbc = Zca = Zejφ, т.е. Zab = Zbc = Zca = Z, φab = φbc = φca = φ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.