Расчет переходных процессов (E=15 В, L=0,2 Гн, C=7 мкФ, R1=400 Ом, R2=200 Ом, R3=600 Ом, ключ размыкается)

Содержание.

1.  Постановка задачи………………………………………………………………………2

2.  Расчёт токов и напряжений классическим методом………………………………….2

3.  Расчёт переходного процесса операторным методом………………………………..5

4.  Сравнение результатов…………………………………………………………………7

5.  Составление системы уравнений по методу переменных состояний……………….7

6.  Графики токов и напряжений………………………………………………………….8

7.  Заключение……………………………………………………………………………...9

8.  Литература………………………...…………………………………………………….10

1.  Постановка задачи.

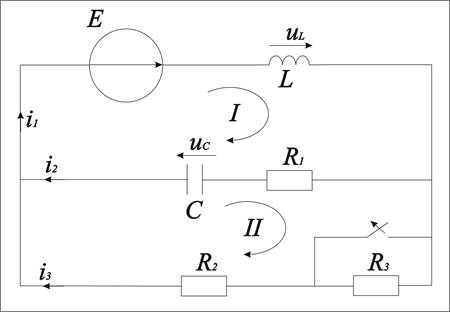
В цепи изображённой на рис.1 происходит коммутация в момент времени t=0(ключ размыкается).

Параметры цепи:

E=15 В

L=0,2 Гн

C=7 мкФ

R1=400 Ом

R2=200 Ом

R3=600 Ом

Рис.1

Требуется: По заданной электрической цепи:

·  Найти законы изменения токов i₁, i₂, i₃и напряжений на емкости u_cи индуктивности u_l классическим методом.

·  Построить временные диаграммы токов i₁, i₂, i₃ и напряжений u_c и u_l.

·  Рассчитать переходный процесс операторным методом.

·  Составить систему уравнений по методу переменных состояния.

2.  Расчёт токов и напряжений классическим методом.

1.  Определение начальных условий.

а) независимые:

б) зависимые

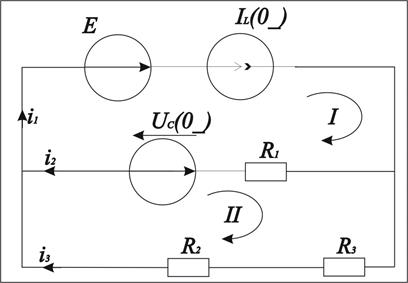
Рис. 2

Составим систему уравнений по законам Кирхгофа для начальных условий

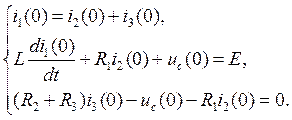
Подставляя данные схемы, получаем

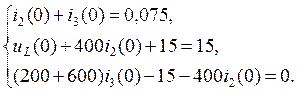
Решая данную систему уравнений, находим зависимые начальные условия.

По закону коммутации, в любой ветви с индуктивностью ток не может изменится скачком и начинает изменяться от значения до коммутации, а напряжение изменяется скачком.

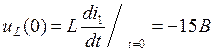       (Напряжение на индуктивности скачком меняется от 0 до )

; .

2.  Система уравнений по законам Кирхгофа.

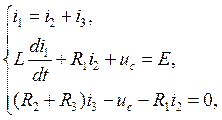                                                                        (1)

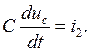 (Уравнение связи)                                                                                                    (2)

Данная система уравнений сводится к одному дифференциальному уравнению второго порядка относительно .

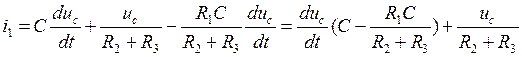
Подставляя результат во второе уравнение системы, получим

.

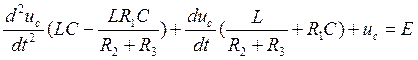3.  Решение дифференциального уравнения.

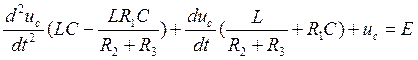
Подставляя числовые значения, получаем

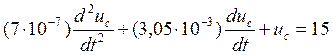
Решение имеет следующий вид:

а) нахождение корней характеристического уравнения (p₁ и p₂).

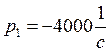
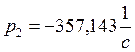
б)Определение постоянных интегрирования (A₁ и A₂).

      =>      

  =>  

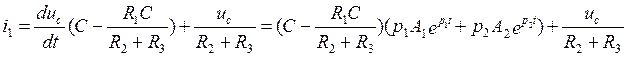
Получаем систему:

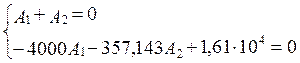
Решение дифференциального уравнения:

4.  Определение остальных токов и напряжений.

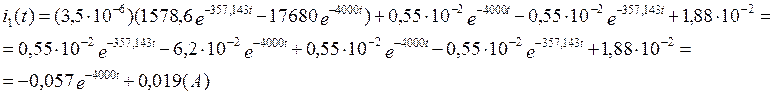
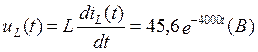
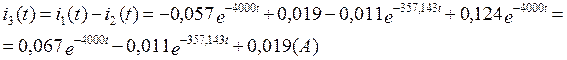                                        (3)

3.  Расчёт переходного процесса операторным методом.

1.  Операторная схема для данной цепи.

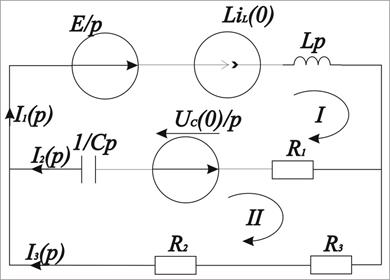
Рис.3

2.  Система уравнений по законам Кирхгофа в операторной форме.

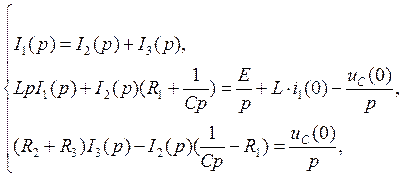
Решая систему нашли

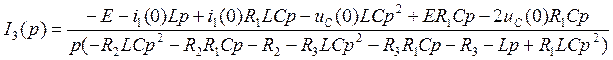
Подставляя силовые значения, имеем

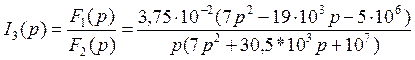
Находи значения параметров.

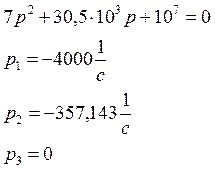
Перейдем от изображения к оригиналу с помощью теоремы разложения.

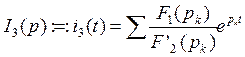
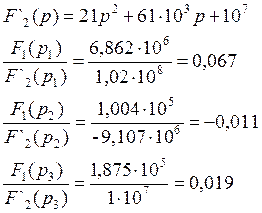
                                                                                (4)

4.  Сравнение результатов.

Ток (3), найденный классическим методом, совпадает с током, найденным операторным методом (4).

5. Составление системы уравнений по методу переменных состояния.

Из системы уравнений (1) и уравнения (2) получим

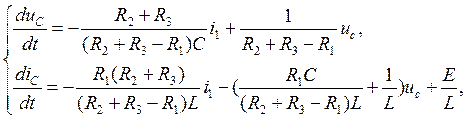
Подставив численные значения величин параметров цепи, получим

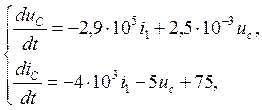
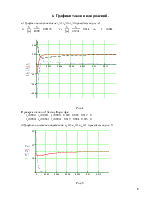
6.  Графики токов и напряжений.

а) Графики изменения токов i₁(t), i₂(t) и i₃(t) приведены на рис. 4.

               =>      

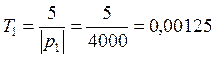
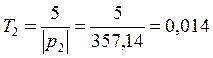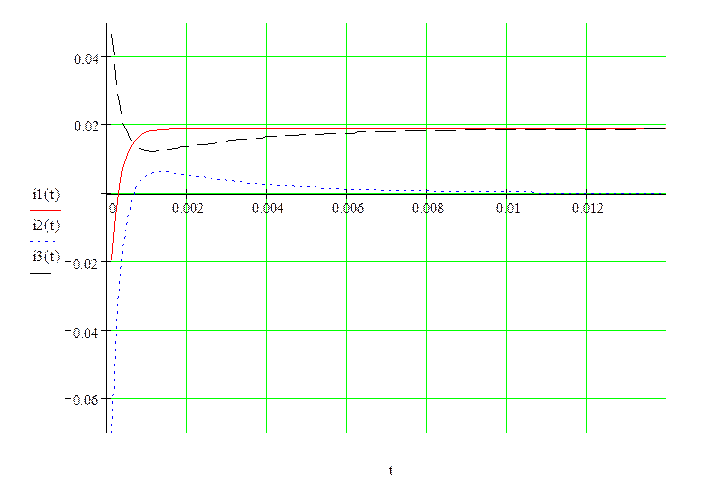
Рис. 4

Проверка токов по 1 Закону Кирхгофа:

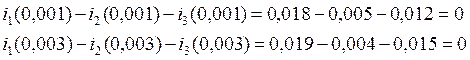
б)Графики изменения напряжений  приведены на рис. 5.

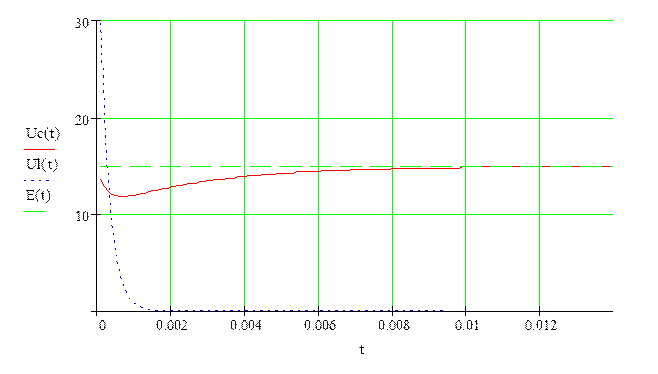
Рис. 5

Проверка напряжений по 2 Закону Кирхгофа:

7. Заключение.

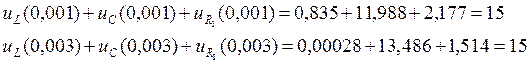
В ходе выполнения работы расчеты переходных процессов производились 2 методами (классическим и операторным), которые дали одинаковые результаты:

Данная работа показывает возможность использования обоих способов для расчёта переходных процессов. С помощью программного пакета Mathcad 2001i Professional были решены системы уравнений и построены графики токов и напряжений.

8. Литература.

1. Методические указания к домашним заданиям по расчету электрических цепей, под редакцией А.П.Лысенко.- Л.: ЛМИ, 1984.
2. Теоретические основы электротехники. Л.А.Бессонов. Москва, 2001.

Приложение.

Как, изменяя сопротивление , можно добиться колебательного процесса в данной схеме?

Для этого необходимо чтобы дискриминант характеристического уравнения

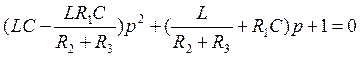 был равен отрицательному числу.

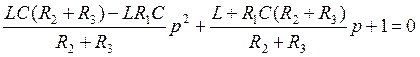
Получим приведённое уравнение

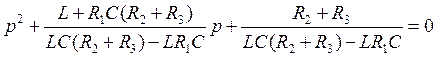
Выразим дискриминант для данного уравнения

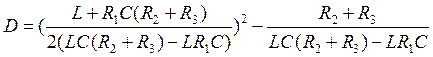
Для того чтобы дискриминант был равен отрицательному числу, необходимо чтобы

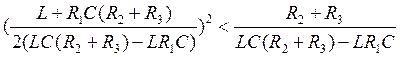
Подставляя численные данные, получаем

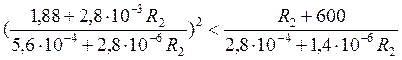
Решая данное неравенство, получаем

Т.к.  решив полученное неравенство, получили, что сопротивление должно быть отрицательным, то значит добиться колебательного процесса в данной схеме, меняя сопротивление , невозможно.