Исследование днищ с различной геометрической формой меридиана, нагруженные постоянным давлением или заполненные жидкостью

Цель работы:

1.  Исследовать характер напряжений в днище;

2.  Определить точку на днищах различной геометрической формы с наибольшими эквивалентными напряжениями;

3.  Выполнить расчет днища МКЭ и сравнить полученные результаты с аналитическим решением.

Объект исследования: днища с различной геометрической формой меридиана, нагруженные постоянным давлением или заполненные жидкостью.

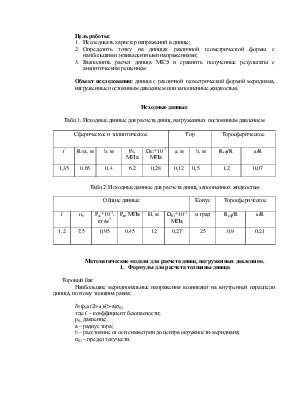
Исходные данные

Табл.1. Исходные данные для расчета днищ, нагруженных постоянным давлением

Сферическое и эллиптическое					Тор		Торосферическое
f	R=a, м	b, м	P0, МПа	Ω02*10-3 МПа	a, м	b, м	Rсф/R	a/R
1,35	0,65	0,4	6.2	0,28	0,12	0,5	1,2	0,07

Табл.2. Исходные данные для расчета днищ, заполненных жидкостью

Общие данные						Конус	Торосферическое
f	nx	Ρж*10-3, кг/м3	Pн, МПа	H, м	Ω02*10-3 МПа	α град	Rсф/R	a/R
1,2	7,5	0,95	0,45	12	0,27	25	0,9	0,21

Математические модели для расчета днищ, нагруженных давлением.

1.  Формулы для расчета толщины днища

  Торовый бак

Наибольшие меридиональные напряжения возникают на внутренней параллели днища, поэтому толщина равна:

δ=fp₀a(2b-a)/(b-a)σ₀₂

где f – коэффициент безопасности;

p_{0 –} давление;

а – радиус тора;

b – расстояние от оси симметрии до центра окружности-меридиана;

σ₀₂ – предел текучести.

  Эллиптическое днище

Если а – большая полуось эллипса, а b – меньшая, то:

δ=fp₀a²/2bσ₀₂ , если а/b<√2;

δ=fp₀a/2σ₀₂(а²/b²-1), если а/b>√2;

Так как эквивалентные напряжения определяются как сумма абсолютных значений тангенциальных и меридиональных напряжений в основании днища, где тангенциальные напряжения отрицательные. В последнем случае следует определять толщину стенки и по верхней точке днища. Окончательное значение толщины в этом случае принимается как наибольшее из двух полученных значений.

  Торосферическое днище.

На торовом участке днища меридиональные напряжения положительные, а тангенциальные – отрицательные, поэтому эквивалентные напряжения определяются по плоскости стыка сферической и торовой оболочек и тогда толщина стенки равна.

δ=fp₀R_сф(R_сф /a-1)/2σ_02, где R_сф – радиус сферического участка днища;

а – радиус торовой части.

  Эллиптическое с жидкостью

Толщина, определяемая по напряжениям в нижней точке днища, равна:

δ=fp₀a²(p₀+ρgn_x(h₀+b))/2bσ_02, где

p₀ – давление жидкости в основании днища, расположенном на расстоянии h₀ от свободной поверхности жидкости;

а, b – большая и малая полуоси эллипса;

ρ – плотность жидкости;

n_x – осевые перегрузки.

  Коническое с жидкостью

Толщина стенки определяется по наибольшим тангенциальным напряжениям, которые возникают в точке экстремума. Координата точки с максимальными тангенциальными напряжениями, измеряемые от основания днища, равна:

X_m = 1/2(H- p₀/ ρgn_x).

Тогда толщина стенки конического днища, заполненного жидкостью, определяется по формуле

δ=f(p₀+ρgn_xx₂)(H-x₂)tgα/ σ₀₂cosα; α – угол полураствора днища, H – его высота, кроме  того, если X_m<0, то в этой формуле следует принять x₂=0, а если X_m>0, то x₂= X_m.

  Торосферическое с жидкостью

Толщина определяется по напряжениям в основании днища. Меридиональные напряжения здесь положительны и равны:

σ₁ = (p₀+Gn_x/πR²)R/2δ, где n_x – осевая перегрузка, G – вес жидкости в днище.

2.  Напряжения в произвольной точке днища

  Торовый бак

σ₁ =fp₀a(2b+asinύ)/2δ(b+asinύ)

σ₂ = fp₀a/2δ,

  Эллиптическое днище

σ₁ =fp₀(m²a²-r²(m²-1))^1/2/2δ

σ₂ = fp₀/δ(m²a²-r²(m²-1))^1/2(1-a²m²/2(m²a²-r²(m²-1)), где

r – радиус параллельного круга,

m=a/b – отношение полуосей эллипса.

  Торосферическое днище

На сферическом участке 0<ύ< ύ₀

 

σ₁ = σ₂ = fp₀R_сф/2δ, на торовом участке ύ₀< ύ<π/2

σ₁ = fp₀R_сф/2δ             σ₂ = fp₀R₂(1- R₂/ 2R₁), где R₁=а, R₂=r/sinύ, r=b+a sinύ.

  Полусферическое с жидкостью

Меридиональные напряжения

σ₁ = fR_сф(p_H+ρgn_x((h+R_сф(2-3cosύ + cos³ ύ))/3 sin² ύ)

Тангенциальные:

σ₂ = f(p_H+ρgn_xh)R₂/ δ  - σ_1, где h=h₀ + R_сф cosύ – высота столба жидкости.

  2.5 Эллиптическое с жидкостью

Меридиональные напряжения

σ₁ =f(p_HR₂/2δ+ ρgn_x R₂[(h₀+x)+(2b-3b²x+x³)/3(b²-x²)]/2δ)

Тангенциальные:

σ₂ =f(p_H+ ρgn_x(h₀+x)) R₂(1- R₂/ 2R₁)/δ - σ₁ R₂/ R_1, где

R₁=(а⁴x²+b⁴r²)^3/2/ а⁴ b⁴           R₂=(а⁴x²+b⁴r²)^1/2/ b²

 

x – расстояние от основания днища до сечения;

p_H - давление на свободной поверхности днища;

h₀ – расстояние от основания днища до поверхности жидкости.

2.6 Коническое с жидкостью

Меридиональные напряжения:

σ₁ =ftgα(p₀+(1/3) ρgn_x(H+2x))(H-x)/2δ

Тангенциальные:

σ₂ =f(p₀+ ρgn_x)(H-x)tgα/ δcosα

Здесь x – расстояние от основания днища до сечения.

2.7 Торосферическое с жидкостью

Меридиональные напряжения:

σ₁ =p₀R₂/2δ+ ρgn_xR₂(x+V(ύ)/πr²)/2δ,

Тангенциальные:

σ₂ = p₀R₂(1- R₂/ 2R₁)/ δ+ ρgn_xR₂[(1- R₂/ 2R₁)x- (R₂/ 2R₁)V/ πR²]/ δ