· Эксплуатационный отказ
3. По характеру изменения параметров, определяющих работоспособность:
· Постепенный
· Внезапный
4. По трудоёмкости устранения:
· Малый (простой до 2 часов)
· Средний (простой от 2 до 4 часов)
· Большой (простой свыше 4 часов)
У исследуемого объекта (2С1 «Гвоздика») могут возникнуть все перечисленные выше виды отказов.
Оценка надёжности 2С19 «МСТА-С» по результатам испытаний
Оценка показателя надёжности 2С11 «Гвоздика» (в данной работе вероятности безотказной работы) производится при помощи пакета прикладных программ OBRIS по результатам условных испытаний. Пакет использует модели испытаний, оперирующие данными типа «успех - отказ – доработка».
Задача определения оценки вероятности безотказной работы (ВБР) разбита на ряд задач:
· подзадача принятия решения об однородности исходной информации;
· подзадача выбора модели испытаний;
· подзадача определения оценок параметров модели испытаний;
· подзадача определения оценок показателей надёжности (ПН) по модели испытаний.
Выполнение задачи осуществляется последовательным решением подзадач без участия оператора.
Задача определения доверительных границ ПН осуществляется отдельно в диалоговом режиме.
Ограничения на применение для программных средств, решающих задачу определения оценки ПН 2С1 по результатам испытаний, следующие:
·
число
серий испытаний ![]() ;
;
· при числе серий испытаний более 3-х исследуемый объект должен иметь устойчивую тенденцию к не уменьшению безотказности к концу испытаний;
· в каждой серии
испытаний число испытаний должно превышать число отказов: ![]() ;
;
· числа испытаний
в различных сериях испытаний не должны отличаться более чем на порядок: ![]() ;
;
·
числа
устранённых причин отказов в различных доработках не должны отличаться более
чем в три-пять раз: ![]() .
.
Ограничения на применение для программных средств, решающих задачу определения доверительных границ в диалоговом режиме:
· оценка верхней доверительной границы (ВДГ) ПН (в отличие от нижней доверительной границы (НДГ)) имеет смысл только для целых значений числа отказов;
· значение доверительной вероятности устанавливается менее 1 и более 0.
Подзадача принятия решения об однородности исходной информации.
Решение подзадачи заключается в нахождении нижних и верхних доверительных границ ВБР в каждой серии испытаний и проверке биномиальной гипотезы для каждой серии. При этом за фиксируемый уровень принимается точечная оценка ВБР, определённая по схеме Бернулли по суммарной наработке всех серий испытаний.
Определение доверительных границ ВБР основано на решении уравнений Клоппера-Пирсона с использованием аппроксимации неполной бета-функцией [5].
Подзадача выбора модели испытаний.
Выбор модели испытаний регламентирован характером исходных данных.
При однородных данных или при единственной серии испытаний принимается биномиальная модель (ГОСТ В20.57.304-76).
При неоднородных данных и не более трёх серий испытаний принимается рекуррентная модель [6].
При неоднородных данных и более трёх серий испытаний принимается аппроксимационная модель [7].
Подзадача определения оценок параметров моделей испытаний.
Определение оценки параметра ![]() рекуррентной модели
рекуррентной модели
![]()
основано на использовании «точного критерия Фишера» (матрицы 2х2).
Определение оценок параметров ![]() аппроксимационной модели
аппроксимационной модели
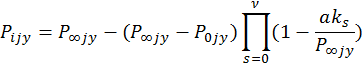
основано на поиске максимума функции максимального правдоподобия.
Подзадача определения оценок ПН по модели испытаний.
Принятая модель испытаний реализуется при вычисленных оценках параметров.
В результате определяются точечная оценка ВБР, точечная оценка средней наработки на отказ, НДГ ВБР, НДГ средней наработки на отказ, эквивалентное число отказов и, при рекуррентной модели, эквивалентное число испытаний.
Входные и выходные данные пакета прикладных программ.
Входными данными задачи определения оценок ПН являются:
· число серий испытаний;
· количество испытаний в каждой серии;
· количество отказов в каждой серии;
· количество причин отказов, устранённых в каждой доработке.
Выходными данными задачи определения оценок ПН являются:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.