Определение скорости монтажного патрона с помощью баллистического крутильного маятника

Лабораторная работа № 13

Определение скорости монтажного патрона с помощью баллистического крутильного маятника.

Цель работы – изучение законов сохранения на примере баллистического крутильного маятника.

Приборы и принадлежности: баллистический крутильный маятник, комплект монтажных патронов, блок миллисекундомера.

Рисунок установки:

Основание 1 оснащено регулируемыми ножками 2, позволяющими выровнять прибор. В основании закреплена колонка 3, на которой закреплены верхний 4, нижний 5 и средний 6 кронштейны. К среднему кронштейну прикреплено стреляющее устройство 7, а также прозрачный экран с нанесенной на него угловой шкалой 8 и фотоэлектрический датчик 9. Кронштейны 4 и 5 имеют зажимы для крепления стальной проволоки 10, на которой подвешен маятник, состоящий из двух мисочек, наполненный пластилином 11, двух перемещаемых грузов 12, двух стержней 13, водилки 14. 

Рабочие формулы:

Период колебания маятника:

,                                                               (1)

где I – момент инерции маятника относительно оси Z

k – коэффициент крутильной жесткости проволоки, где, где

l – длина однородной проволоки,

R – радиус круглого сечения,

G – модуль сдвига материала проволоки.

, где М_кр – момент кручения проволоки,

 - угол поворота маятника.

                                                               (2)

E_p – потенциальная энергия упругодеформированной проволоки при кручении.

Учитывая пренебрежительно малую величину момента сил трения при движении крутильного маятника, можно говорить о законе сохранения механической энергии, т.е. при колебании маятника кинетическая энергия вращательного движения системы превращается в потенциальную энергию (2) упругодеформированной проволоки при кручении:

                                                               ,                                                               (3)

где  - момент инерции маятника вместе с попавшим в него патроном (согласно теореме Штейнера), где

I₁ – момент инерции собственно маятника относительно вертикальной оси,

m – масса патрона,

r – расстояние от оси вращения до точки удара патрона,

 - угловая скорость маятника.

При определении угловой скорости воспользуемся законом сохранения момента импульса:

,

при mr² <<I₁

.

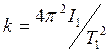
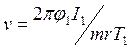                                                                                                                      (4)

Если подвижные грузы максимально удалить друг от друга, то по теореме Штейнера момент инерции маятника

,                                                             (5)

а его период колебаний

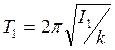
Если грузы разместить вплотную, то

,                                                            (6)

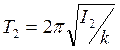, где I₀ – момент инерции маятника, когда центр тяжести грузов совпадает с осью вращения маятника,

I₁ – момент инерции маятника, когда грузы находятся на расстоянии r₁,

I₂ – момент инерции маятника, когда грузы находятся на расстоянии r₂,

M – масса груза,

r₁ – расстояние от оси вращения до центра масс груза в первом положении,

r₂ – расстояние от оси вращения до центра масс груза во втором положении.

Вычитая (6) из (5), получаем

.

С учетом 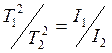, исключая из последнего выражения I₂:

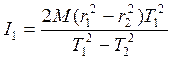                                                          (7)

Подставляя (7) в (4), получаем скорость монтажного патрона

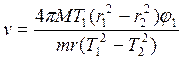, где  - максимальный угол отклонения, когда оба груза расположены на расстоянии r₁ (рад).

Расчет погрешностей измерений

Таблица прямых измерений

r=0,12 м                          m=0,0037 кг                          M=0,193 кг                

№ опыта	r1=0,09 м				r1=0,02 м				v
			t1	T1			t2	T2
	град	рад	с		град	рад	с		м/с
1.	20°	0,349	18,319	6	40°	0,697	7,497	5	8
2.	30°	0,523	20,262	8	36°	0,628	6,974	4	3,66
3.	27°	0,471	19,843	7	38°	0,663	7,001	5	5,78
4.	25°	0,436	19,276	7	39°	0,680	7,173	5	5,35
5.	29°	0,506	20,138	8	37°	0,645	7,021	4	3,55

v_ср=5,268 м/с

i	, м/с	, м/с
1.	8,00	2,73	7,45
2.	3,66	1,61	2,59
3.	5,78	0,51	0,26
4.	5,35	0,08	0,01
5.	3,55	1,72	2,96
	м/с	м/с	м/с

1. В процессе измерений были исключены известные систематические ошибки. Можно считать, что постоянные систематические погрешности дают пренебрежимо малый вклад в результат наблюдений. Таким образом, серию результатов считаем исправленными результатами наблюдений.

2. Вычисляем среднее арифметическое скорости:

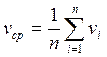
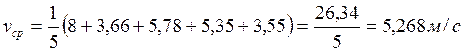
3. Промахи в данной серии отсутствуют, так как максимальное отклонение от среднего (в первом наблюдении) не превосходит в 2,5 раза среднюю абсолютную погрешность по разбросу. Средняя погрешность по разбросу:

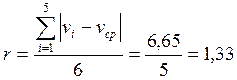
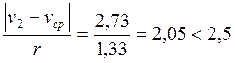
4. Вычисляем оценку среднего квадратического отклонения результатов измерений

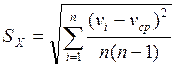
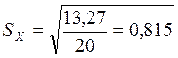
5. Так как n<15, считаем распределение нормальным.

6.Определяем доверительные границы случайной погрешности

, где (n) – коэффициент Стьюдента в зависимости от надежности и числа