The results of fitting an exponential distribution to the data on EXP

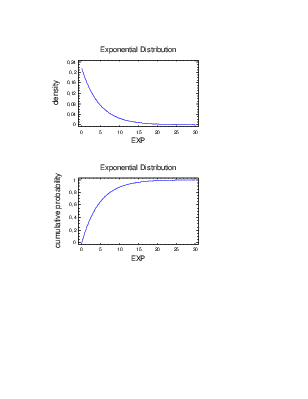
Uncensored Data - EXP

Analysis Summary

Data variable: EXP

100 values ranging from 0,0746175 to 28,8372

Fitted exponential distribution:

mean = 4,65513

The StatAdvisor

--------------This analysis shows the results of fitting an exponential

distribution to the data on EXP.  The estimated parameters of the

fitted distribution are shown above.  You can test whether the

exponential distribution fits the data adequately by selecting

Goodness-of-Fit Tests from the list of Tabular Options.  You can also

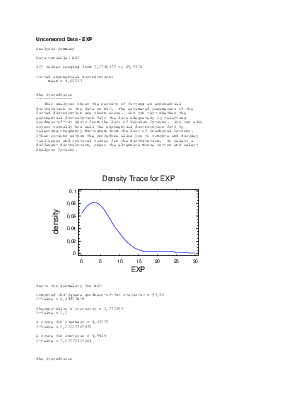
assess visually how well the exponential distribution fits by

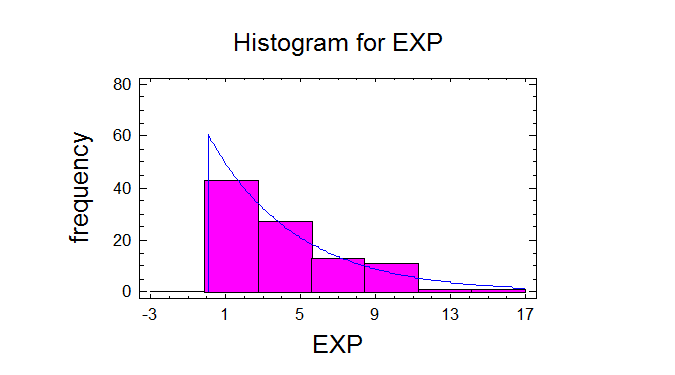
selecting Frequency Histogram from the list of Graphical Options.

Other options within the procedure allow you to compute and display

tail areas and critical values for the distribution.  To select a

different distribution, press the alternate mouse button and select

Analysis Options.

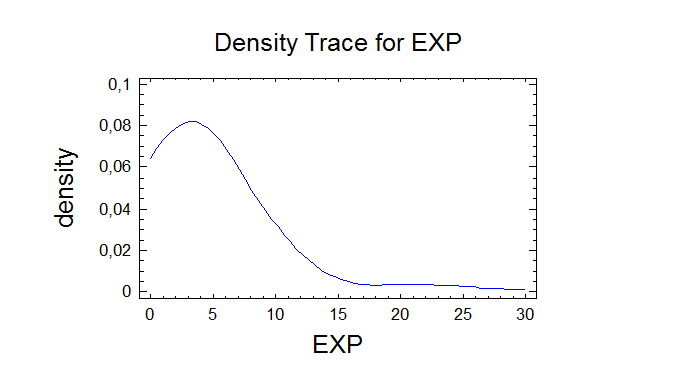
Tests for Normality for EXP

Computed Chi-Square goodness-of-fit statistic = 83,36

P-Value = 2,19907E-9

Shapiro-Wilks W statistic = 0,770183

P-Value = 0,0

Z score for skewness = 4,63005

P-Value = 0,00000365975

Z score for kurtosis = 4,8914

P-Value = 0,00000100261

The StatAdvisor

--------------This pane shows the results of several tests run to determine

whether EXP can be adequately modeled by a normal distribution.  The

chi-square test divides the range of EXP into 24 equally probable

classes and compares the number of observations in each class to the

number expected.  The Shapiro-Wilks test is based upon comparing the

quantiles of the fitted normal distribution to the quantiles of the

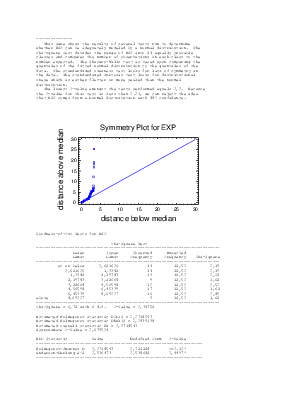
data.  The standardized skewness test looks for lack of symmetry in

the data.  The standardized kurtosis test looks for distributional

shape which is either flatter or more peaked than the normal

distribution.

The lowest P-value amongst the tests performed equals 0,0.  Because

the P-value for this test is less than 0.01, we can reject the idea

that EXP comes from a normal distribution with 99% confidence.

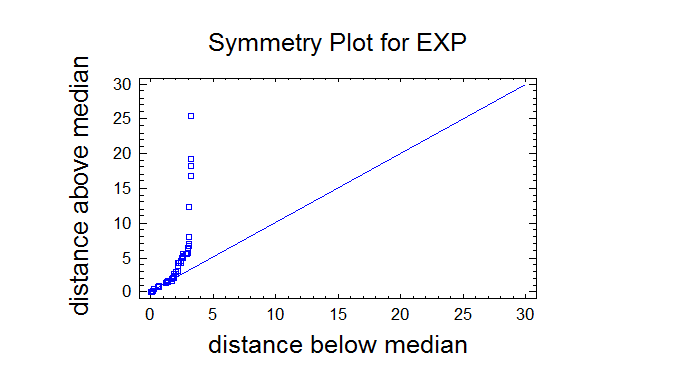
Goodness-of-Fit Tests for EXP

Chi-Square Test

---------------------------------------------------------------------------Lower         Upper      Observed      Expected

Limit         Limit     Frequency     Frequency    Chi-Square

---------------------------------------------------------------------------at or below      0,621606            14         12,50          0,18

0,621606        1,3392            14         12,50          0,18

1,3392       2,18793            13         12,50          0,02

2,18793       3,22669             8         12,50          1,62

3,22669       4,56589            10         12,50          0,50

4,56589       6,45338            17         12,50          1,62

6,45338       9,68007            16         12,50          0,98

above        9,68007                           8         12,50          1,62

---------------------------------------------------------------------------Chi-Square = 6,72 with 6 d.f.   P-Value = 0,34752

Estimated Kolmogorov statistic DPLUS = 0,0719543

Estimated Kolmogorov statistic DMINUS = 0,0438139

Estimated overall statistic DN = 0,0719543

Approximate P-Value = 0,678504

EDF Statistic          Value           Modified Form   P-Value

--------------------------------------------------------------------Kolmogorov-Smirnov D   0,0719543       0,721229        >=0.10*

Anderson-Darling A^2   0,536473        0,539692        0,4487*

--------------------------------------------------------------------*Indicates that the P-Value has been compared to tables of critical values

specially constructed for fitting the currently selected distribution.

Other P-values are based on general tables and may be very conservative.

The StatAdvisor

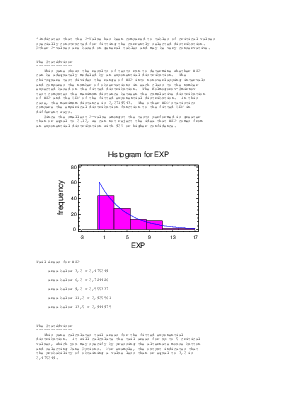
--------------This pane shows the results of tests run to determine whether EXP

can be adequately modeled by an exponential distribution.  The

chi-square test divides the range of EXP into nonoverlapping intervals

and compares the number of observations in each class to the number

expected based on the fitted distribution.  The Kolmogorov-Smirnov

test computes the maximum distance between the cumulative distribution

of EXP and the CDF of the fitted exponential distribution.  In this

case, the maximum distance is 0,0719543.  The other EDF statistics

compare the empirical distribution function to the fitted CDF in

different ways.

Since the smallest P-value amongst the tests performed is greater

than or equal to 0.10, we can not reject the idea that EXP comes from

an exponential distribution with 90% or higher confidence.

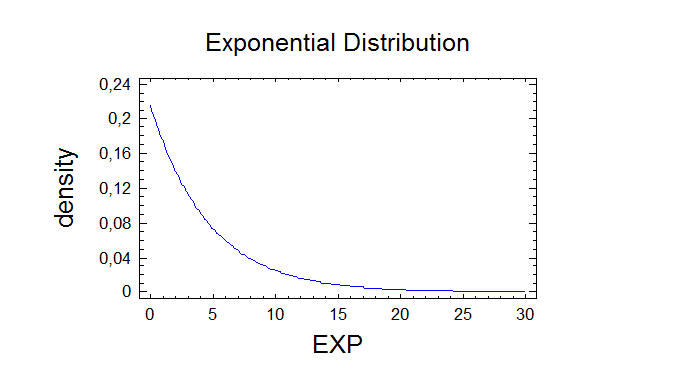
Tail Areas for EXP

area below 3,0 = 0,475049

area below 6,0 = 0,724426

area below 9,0 = 0,855337

area below 11,0 = 0,905861

area below 13,5 = 0,944978

The StatAdvisor

--------------This pane calculates tail areas for the fitted exponential

distribution.  It will calculate the tail areas for up to 5 critical

values, which you may specify by pressing the alternate mouse button

and selecting Pane Options.  For example, the output indicates that

the probability of obtaining a value less than or equal to 3,0 is

0,475049.

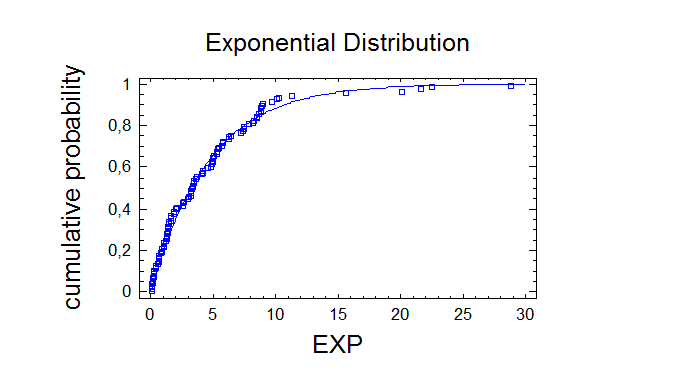
Critical Values for EXP

area below 0,0467856 = 0,01

area below 0,490467 = 0,1

area below 3,22669 = 0,5

area below 10,7188 = 0,9

area below 21,4377 = 0,99

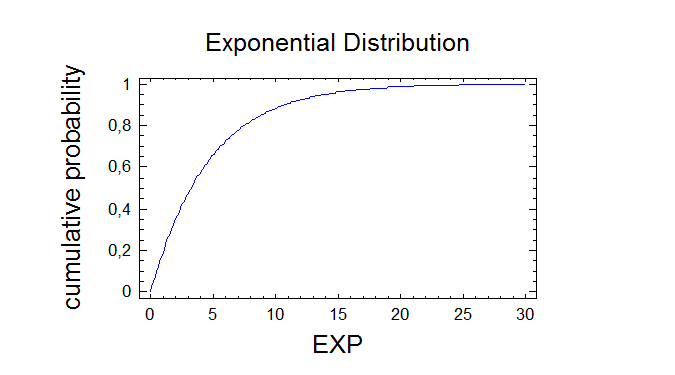
The StatAdvisor

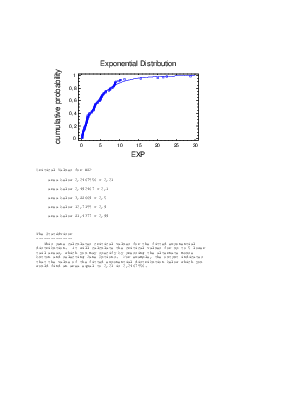
--------------This pane calculates critical values for the fitted exponential

distribution.  It will calculate the critical values for up to 5 lower

tail areas, which you may specify by pressing the alternate mouse

button and selecting Pane Options.  For example, the output indicates

that the value of the fitted exponential distribution below which you

would find an area equal to 0,01 is 0,0467856.