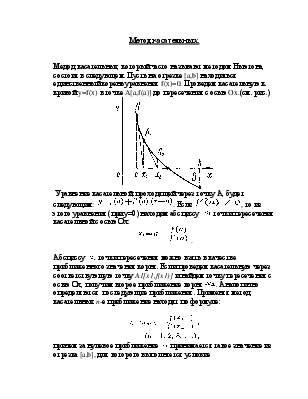

Метод касательных.
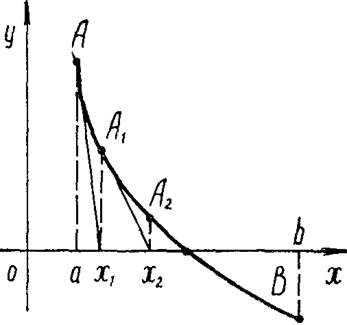
Медод касательных, который часто называют методом Ньютона, состоит в следующем. Пусть на отрезке [a,b] находиться единственный корень уравнения f(x)=0. Проведем касательную к кривой y=f(x) в точке A[a,f(a)] до пересечения с осью Ox.(см. рис.)
Уравнение касательной,
проходящей через точку А, будет следующим: ![]() . Если
. Если![]() ,
то из этого уравнения (при у=0) находим абсциссу
,
то из этого уравнения (при у=0) находим абсциссу ![]() точки
пересечения касательной с осью Ох:
точки
пересечения касательной с осью Ох:
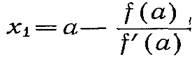 .
.
Абсциссу ![]() точки
пересечения можно взять в качестве приближенного значения корня. Если проведем
касательную через соответствующую точку A1[x1,f(x1)] и найдем точку пересечения с осью Ох, получим второе
приближение корня
точки
пересечения можно взять в качестве приближенного значения корня. Если проведем
касательную через соответствующую точку A1[x1,f(x1)] и найдем точку пересечения с осью Ох, получим второе
приближение корня![]() . Аналогично
определяются последующие приближения. Применяя метод касательных n-е
приближение находят по формуле:
. Аналогично
определяются последующие приближения. Применяя метод касательных n-е
приближение находят по формуле:
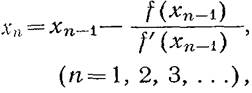
причем за нулевое приближение
![]() принимается такое значение из отрезка [a,b], для
которого выполняется условие
принимается такое значение из отрезка [a,b], для
которого выполняется условие
![]()
Вычисления проводят до тех пор, пока не перестанут изменятся сохраняемые в ответе десятичные знаки. Для промежуточных выкладок надлежит брать один-два запасных знака. Оценка погрешности определяется формулой
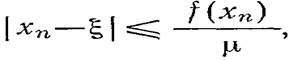
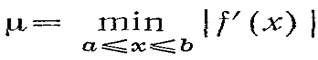
Приближенное вычисление корня по методу касательных, определение номера n приближения xn, при котором будет достигнута заданная точность, можно осуществить на основе следующей теоремы.
Пусть для уравнения f(x)=0 и начального приближения x0 искомого корня выполняются условия:
1)
![]() ≠A и
≠A и ![]()
2)
![]()
3)
![]() на отрезке
на отрезке
![]()
4)
![]()
5)
![]()
Тогда
данное уравнение имеет корень ![]() , принадлежащий
отрезку
, принадлежащий
отрезку ![]() . Этот корень может быть получен как предел
последовательности каждый член которого находится по формуле
. Этот корень может быть получен как предел
последовательности каждый член которого находится по формуле
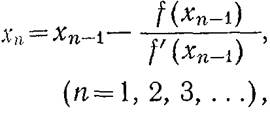
Оценка погрешности определяется по формуле
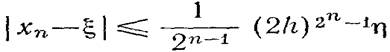
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.