Составление математической модели движения груза по заданной наклонной плоскости под действием силы. Построение графиков функций движения, скорости и ускорения тела

         Глава 2.    Математическое моделирование

2.1  Постановка задачи

Телу массой m сообщена начальная скорость V₀,направленная вверх по наклонной плоскости. На тело действует сила P, заданна кусочно-непрерывной  функцией и направленная в ту же сторону (рис.1.а, б). Параметры зависимости силы P(t) и коэффициент трения скольжения f представлены в таблице 2.1. Данные о  наклонной плоскости (рис.1.б) приведены в таблице 2.2.

    Таблица 2.1 Исходные данные к заданию

где t1,t2,t3 – моменты времени изменения силы P(t).(t0=0).

    Таблица 2.2 Параметры наклонной плоскости

где x1,x2- длина участка с углом наклона α1  , α2  соответственно.

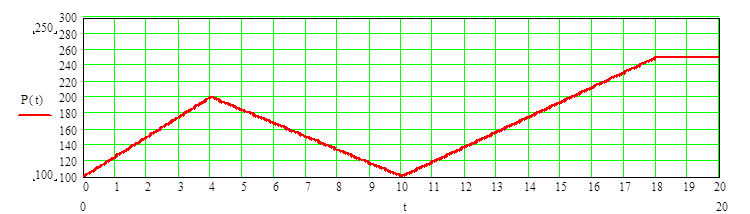
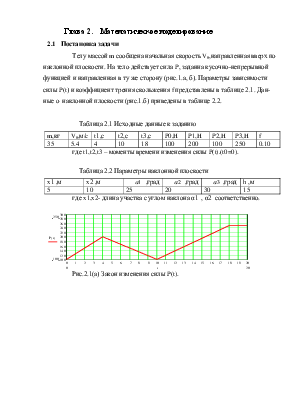
Рис.2.1(а) Закон изменения силы P(t).

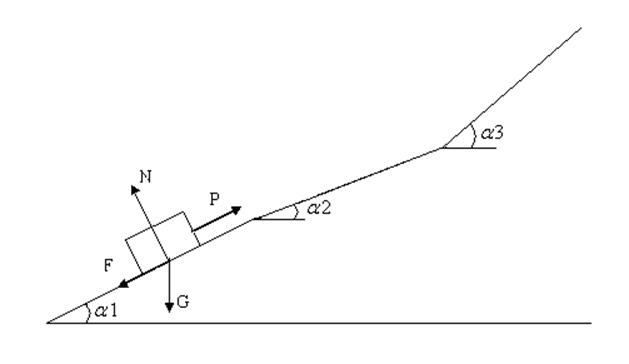
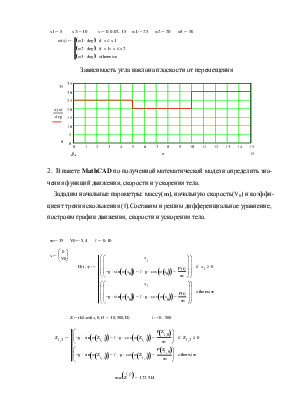
Рис.2.1(б). Форма наклонной плоскости.

Необходимо:

1.  Составить математическую модель движения груза по заданной наклонной плоскости под действием силы P(t);

2.  В пакете MathCAD по полученной математической модели определить значение функций движения, скорости и ускорение тела;

3.  Построить графики функций движения, скорости и ускорения тела;

4.  С помощью пакета MathCoonex выполнить моделирование влияния начальной скорости на движение тела и определить минимальную начальную скорость V_{0 min} , при которой тело поднимается на заданную высоту h;

5.  Для найденной начальной скорости V_{0 min} построить графики функций движения, скорости и ускорения тела.

2.2  Составление математической модели.

Покажем силы, действующие на тело (рис.2.1(б)): вес G, нормальную реакцию плоскости N, силу P и силу трения скольжения F, направив ее противоположно начальной скорости, т.е. вниз по наклонной плоскости.

Построим график P=P(t) по заданным значениям P₀, P₁, P₂ и P₃ (рис. 2.1(а)).

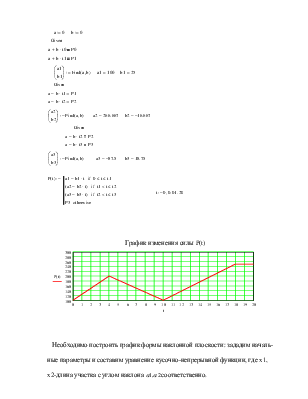
Запишем дифференциальное уравнение для тела, принимаемого за материальную точку: 

Раскроем правую часть уравнения:

Учитывая, что сила трения скольжения  , получаем

т.е. 

.

Подготовим уравнение к решению в MathCAD, для этого необходимо ввести следующие зависимые переменные:  и . Уравнение в MathCAD имеет вид:            

Данное дифференциальное уравнение используется при движении заданного тела вверх. 

Если тело движется вниз, то уравнение будет иметь следующий вид:

2.3. Вычисление дифференциального уравнения в пакете MathCAD.

1.  Составим математическую модель движения груза по заданной наклонной плоскости под воздействием силы P(t).

t1, t2, t3-моменты времени изменения силы P1, P2, P3 соответственно .

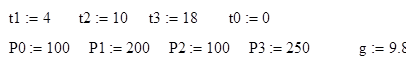
Зададим  начальные условия кусочно- непрерывной функции и построим график изменения силы P(t).

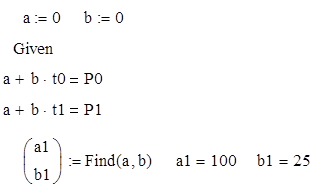
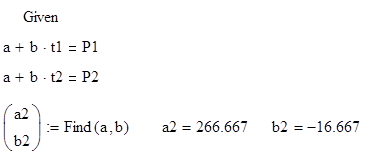
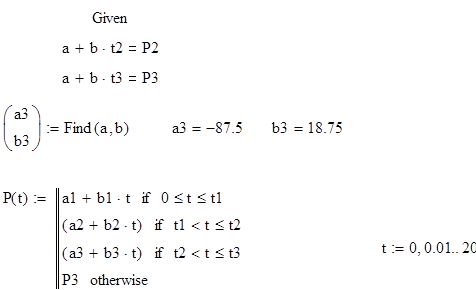
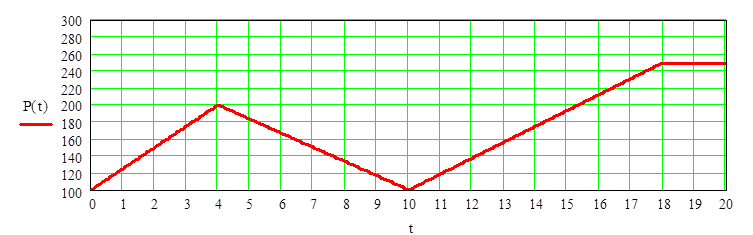
График изменения силы P(t) 

Необходимо построить график формы наклонной плоскости: зададим начальные параметры и составим уравнение кусочно-непрерывной функции, где x1, x2-длина участка с углом наклона соответственно.

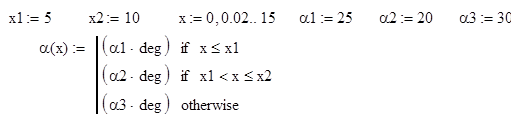
Зависимость угла наклона плоскости от перемещения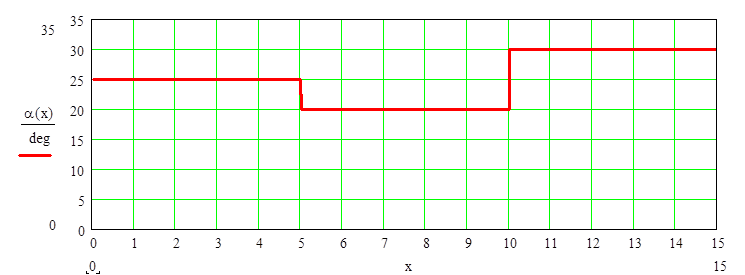      

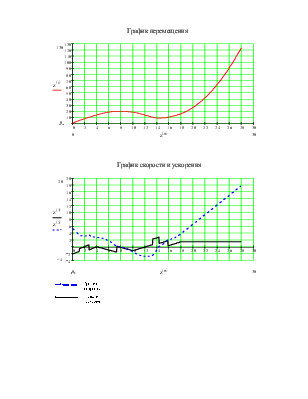
2.  В пакете MathCAD по полученной математической модели определить значения функций движения, скорости и ускорения тела.

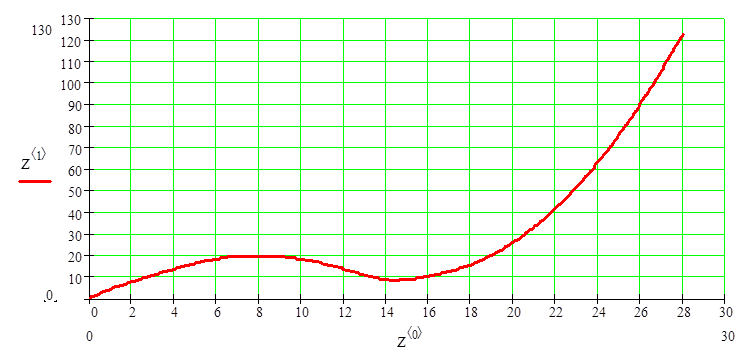
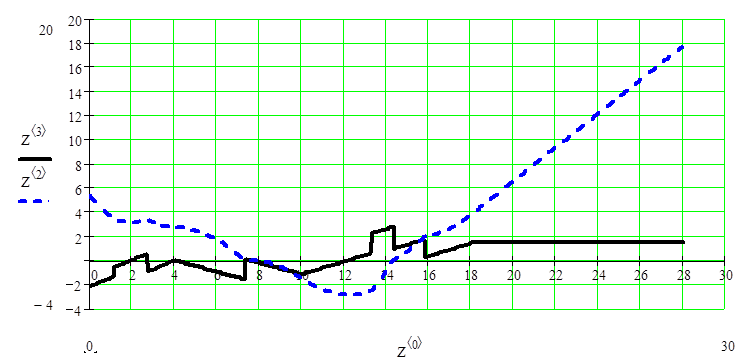
Зададим начальные параметры: массу(m), начальную скорость(V₀) и коэффициент трения скольжения (f).Составим и решим дифференциальное уравнение, построим график движения, скорости и ускорения тела. 

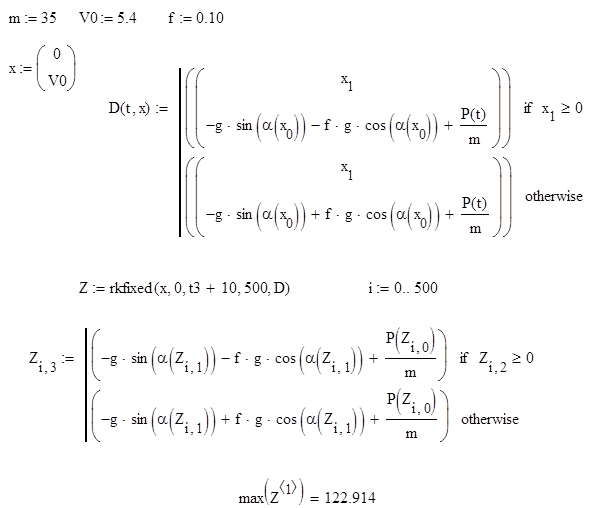
График перемещения

                                          График скорости и ускорения