Министерство образования
Республики Беларусь
Учреждение образования
«Гомельский государственный технический университет им. П.О. Сухого»
Кафедра: «Технология машиностроения»
Лабораторная работа №1.
«Средства MicrosoftOffice в математической обработке данных эксперимента с помощью латинских квадратов».
Выполнил студент гр. ТМ-41
Яськов А.В.
Принял преподаватель
Мурашко В.С.
Гомель 2003
Лабораторная работа №1.
«Средства MicrosoftOffice в математической обработке данных эксперимента с помощью латинских квадратов».
Цель работы: с помощью средств Microsoft Office: Word и Excel автоматизировать математическую обработку данных эксперимента.
1.Изучить краткие теоретические сведения о планировании эксперимента с помощью четырех факторного дисперсионного анализа – «латинских квадратов» и метод наименьших квадратов.
С помощью Excel для заданного латинского квадрата определить, какие из четырех факторов A, B, C, D значимы.
2.Упростить эмпирическую функцию
определения значений эксперимента ![]() , отбросив
сомножители, содержащие незначимые факторы.
, отбросив
сомножители, содержащие незначимые факторы.
3.Для полученной
своей математической модели определить неизвестные параметры методом наименьших
квадратов. Для этого необходимо с помощью Excel
решить систему линейных уравнений (методом обратной матрицы), в
которую входят:
· два уравнения, если значим один фактор;
· три уравнения, если значим два фактора;
· четыре уравнения, если значим три фактора;
· пять уравнений, если значим четыре фактора.
4.С помощью Excel построить графики результатов эксперимента и значения эксперимента по эмпирической модели.
5.EXCEL: сортировка, авто фильтр, сводная таблица, подведение итогов для латинских квадратов. Методика прилагается к заданию.

Обозначив через xij наблюдение, полученное при уровнях основных факторов Аi , Bj , найдем сумму квадратов всех наблюдений Q1
Q1=
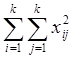
Найдем сумму квадратов итогов по столбцам, деленную на к:
Q2=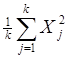
Найдем сумму квадратов итогов по строкам, деленную на к:
Q3=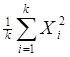
Найдем сумму квадрат общего итога, деленный на к2:
Q4=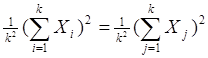
Найдем сумму квадратов итогов по уровням фактора С, деленную на к:
Q5=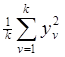 ,
,
Yv – сумма всех наблюдений, проводившихся на уровне Сv фактора С независимо от того, каким при этом были уровни факторов A, B, D.
Найдем сумму квадратов итогов по уровням фактора D, деленную на к:
Q6=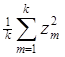
zm – сумма всех наблюдений, проводившихся на уровне Dm фактора D независимо от того, каким при этом были уровни факторов A, B, C.
Совместная дисперсия воспроизводимости и взаимодействия
![]()
Определим выборочные дисперсии факторов A, B, C, D:
![]()
![]()
![]()
![]()
![]()
Определим отношения ![]()
![]()
![]()
![]()
Определим значимость основных факторов по критерию Фишера. Для этого определим значение квантиля Fi для уровня значимости 0.05 при f1=3, f2=3: Fi-p=9.3.
Если Si/S0 больше: Fi-p=9.3.
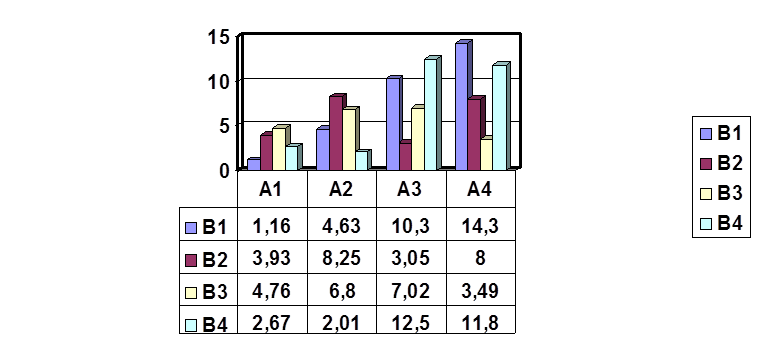
Таблица 1.-Латинский квадрат.
|
Уровни факторов А. |
Xi |
||||
|
A1 |
A2 |
A3 |
A4 |
||
|
B1 |
1,16 |
4,63 |
10,3 |
14,3 |
30,39 |
|
B2 |
3,93 |
8,25 |
3,05 |
8 |
23,23 |
|
B3 |
4,76 |
6,8 |
7,02 |
3,49 |
22,07 |
|
B4 |
2,67 |
2,01 |
12,5 |
11,8 |
28,98 |
|
Xj |
12,52 |
21,69 |
32,87 |
37,59 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.