Выбираем резисторы типа МЛТ - 0.125 номиналом:
R8 = R7 = 16кОм R1 = R2 = 100кОм R4 = R3 = 20кОм
R6 = R5 = 10кОм R9 = R10 = 20кОм
Выбираем диоды КД 102 Д
Во втором канале используем такой же модулятор.
Все используемые в схемах операционные усилители принимаем типа К140УД-15
Для того, чтобы убрать все помехи используем полосовые фильтры. Поскольку необходимо обеспечить достаточно узкий диапазон частот, который необходимо оставить без изменения, в качестве полосового фильтра выбираем активный полосовой фильтр Чебышева.
Добротность фильтра равна 10. Уровни, ограничивающие боковые спуски ЛАЧХ фильтра, равны 3 и 30 дБ.
Для первого сигнала будем выделять нижнюю боковую полосу, которая обрезает центром на частоте:
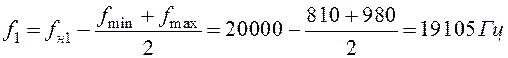
Диапазон среза ЛАЧХ фильтра равенTW = 1200 Гц
Поправочный коэффициент равен:
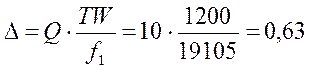
Диапазон среза равен:
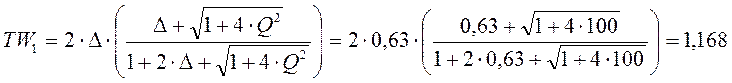
Порядок низкочастотного фильтра равен:
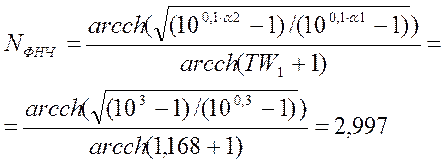 (2.5.1)
(2.5.1)
Следовательно, необходимый порядок полосового фильтра равен:
![]()
Ближайшее четное число 6, значит, полосовой фильтр будет состоять из трех звеньев высшего порядка. Схема такого звена приведена на рисунке 2.5.1
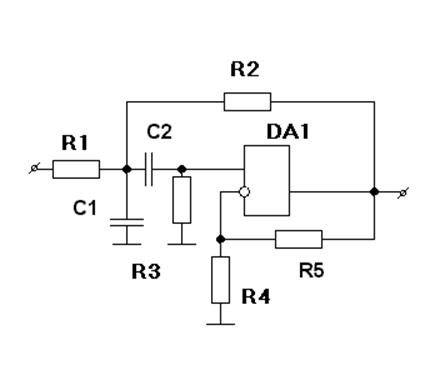
Рисунок 2.5.1 - Звено высшего порядка для фильтра Чебышева
Коэффициенты Чебышева в данном случае равны:
В = 0,6449; С = 0,707948
Вспомогательные величины:
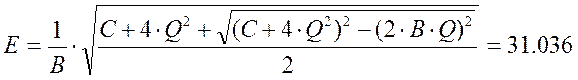 (2.5.2)
(2.5.2)
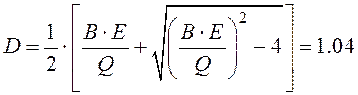 (2.5.3)
(2.5.3)
При коэффициенте усиления фильтра равном 1, постоянные фильтра равны:
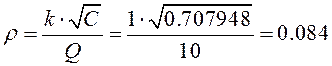 (2.5.4)
(2.5.4)
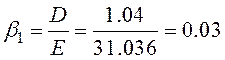 (2.5.5)
(2.5.5)
![]() (2.5.6)
(2.5.6)
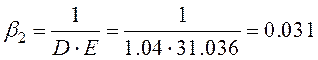 (2.5.7)
(2.5.7)
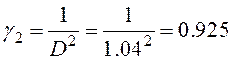 (2.5.8)
(2.5.8)
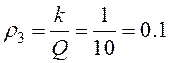 (2.5.9)
(2.5.9)
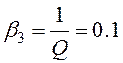 (2.5.10)
(2.5.10)
![]() (2.5.11)
(2.5.11)
Учитывая, что ![]() запишем передаточную функцию
полосового фильтра:
запишем передаточную функцию
полосового фильтра:
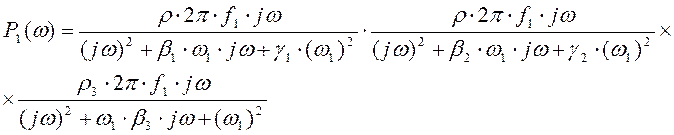
ЛАЧХ полосового фильтра построена в Приложении А.
Рассчитаем элементы первого звена
фильтра с параметрами![]() :
:
Емкость конденсаторов С1 и С2 равна:
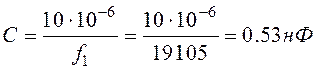 (2.5.12)
(2.5.12)
Принимаем конденсатор КМ-6-510пФ-25В
Принимаем ![]() ,
тогда сопротивления равны:
,
тогда сопротивления равны:
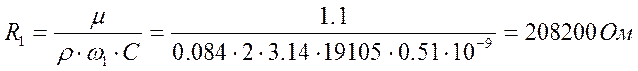 (2.5.13)
(2.5.13)
Принимаем резистор равным: МЛТ – 0.125 – 200к
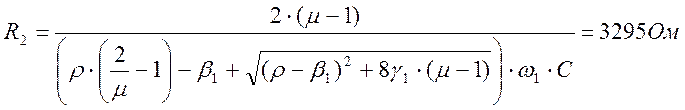 (2.5.14)
(2.5.14)
Принимаем резистор равным: МЛТ-0.125 - 3,3к
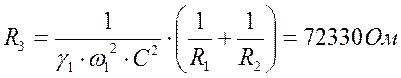 (2.5.15)
(2.5.15)
Принимаем резистор равным: МЛТ – 0,125 – 75к
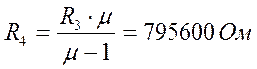 (2.5.16)
(2.5.16)
Принимаем резистор равным: МЛТ – 0,125 – 820к
![]() (2.5.17)
(2.5.17)
Принимаем резистор равным: МЛТ – 0,125 – 82к
Так как резисторы выбраны из ряда Е24, то тогда рассчитаем параметры фильтра с учетом выбранных сопротивлений:
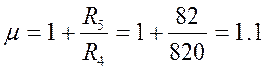 (2.5.18)
(2.5.18)
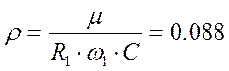 (2.5.19)
(2.5.19)
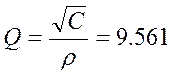 (2.5.20)
(2.5.20)
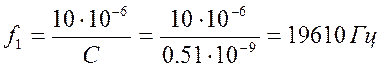 (2.5.21)
(2.5.21)
Аналогично рассчитываются элементы
второго звена фильтра с параметрами ![]() :
:
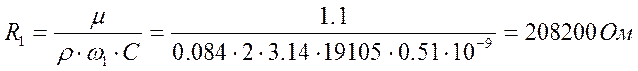 (2.5.22)
(2.5.22)
Принимаем резистор равным: МЛТ – 0.125 –200к
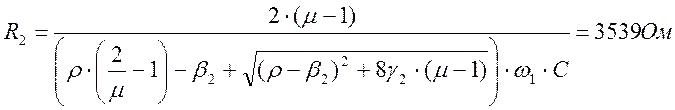 (2.5.23)
(2.5.23)
Принимаем резистор равным: МЛТ-0.125-3,6к
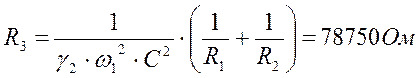 (2.5.24)
(2.5.24)
Принимаем резистор равным: МЛТ – 0,125 – 82к
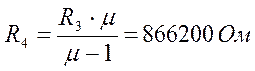 (2.5.25)
(2.5.25)
Принимаем резистор равным: МЛТ – 0,125 – 910к
![]() (2.5.26)
(2.5.26)
Принимаем резистор равным: МЛТ – 0,125 – 91к
Элементы третьего звена
рассчитывают по формулам с параметрами![]() :
:
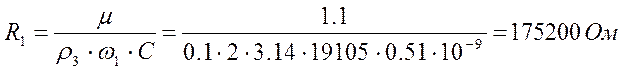 (2.5.27)
(2.5.27)
Принимаем резистор равным: МЛТ – 0.125 –180к
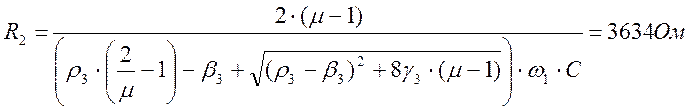 (2.5.28)
(2.5.28)
Принимаем резистор равным: МЛТ-0.125-3,6к
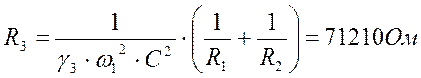 (2.5.29)
(2.5.29)
Принимаем резистор равным: МЛТ – 0,125 – 75к
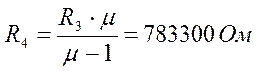 (2.5.30)
(2.5.30)
Принимаем резистор равным: МЛТ – 0,125 – 820к
![]() (2.5.31)
(2.5.31)
Принимаем резистор равным: МЛТ – 0,125 – 82к
![]()
Аналогично для второго сигнала вычисляем центральную частоту для верхней боковой полосы:
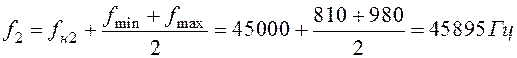
Диапазон среза ЛАЧХ фильтра равен TW = 3000 Гц
Поправочный коэффициент равен:
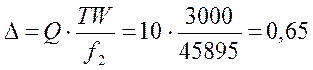
Диапазон среза равен:
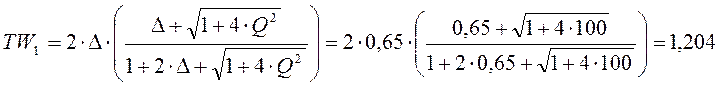
Порядок низкочастотного фильтра равен:
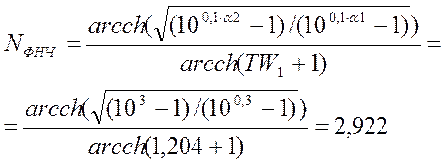 (2.5.32)
(2.5.32)
Следовательно, необходимый порядок полосового фильтра равен:
![]()
Ближайшее четное число 6, а значит, полосовой фильтр будет состоять из трех звеньев высшего порядка.
Коэффициенты Чебышева в данном случае равны:
В = 0,6449; С = 0,707948
Вспомогательные величины:
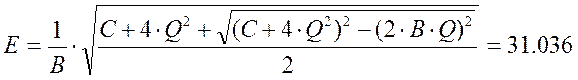
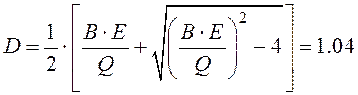
При коэффициенте усиления фильтра равном 1, постоянные фильтра равны:
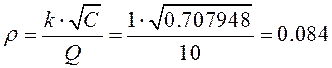
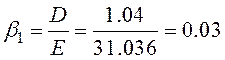
![]()
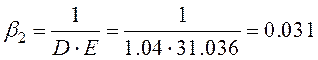
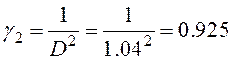
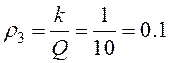
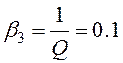
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.