Анализ переходных процессов в гидросистемах. Пример расчета переходных процессов в объемном гидроприводе, страница 2

суммарные потери напора на других местных сопротивлениях напорной магистрали (колена, тройники, выход из трубы в гидроаппараты и т.д.):

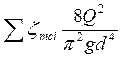
=,                                           (12)

-коэффициенты местных сопротивлений;

- инерционный напор жидкости в напорной магистрали:

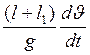=.                                                         (13)

·  Для сливной магистрали (от сечения 2-2 гидроцилиндра до точки 3)

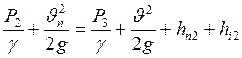,                                               (14)

где - давление в гидробаке ();

- давление жидкости в правой полости гидроцилиндра;

- потери напора в сливной магистрали:

=;                                              (15)

- потери напора в гидролиниях сливной магистрали:

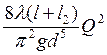
=;                                                  (16)

- суммарные потери напора на других местных сопротивлениях сливной магистрали;

- инерционный напор жидкости в сливной магистрали:

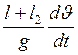=.                                                          (17)

Уравнение баланса сил, действующих на поршень гидроцилиндра при неустановившемся движении:

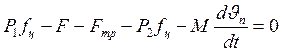,                                         (18)

где =(1-)F – сила трения в гидроцилиндре;

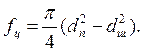
Используя выражение (13), (14), (17), (18) уравнение (6) приводится к виду:

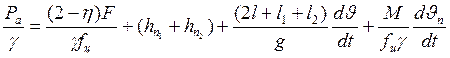                                 (19)

Учитывать связь:

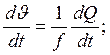
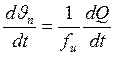                                                  (20)

и выражения (7), (8), (9), (10), (11), (12), (15), (16) уравнение (19) записывается в виде:

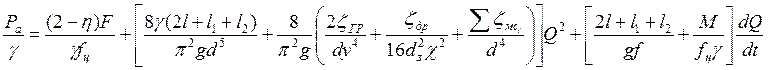          (21)

Обозначим:

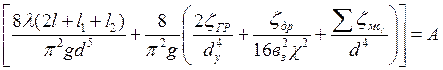                                   (22)

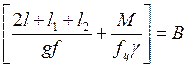                                                         (23)

Тогда уравнение (21) можно записать в виде:

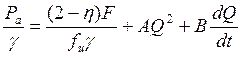                                                          (24)

Уравнение (24):

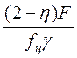 - статический напор;

 - потери напора в гидролиниях и гидроаппаратах;

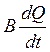 - полный инерционный напор.

На рисунке 4 линия I выражает зависимость суммы напоров 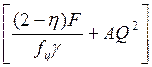 от расхода жидкости Q.

Линия 2 представляет характеристику насосного агрегата, т. е. зависимость давления P_a от Q.

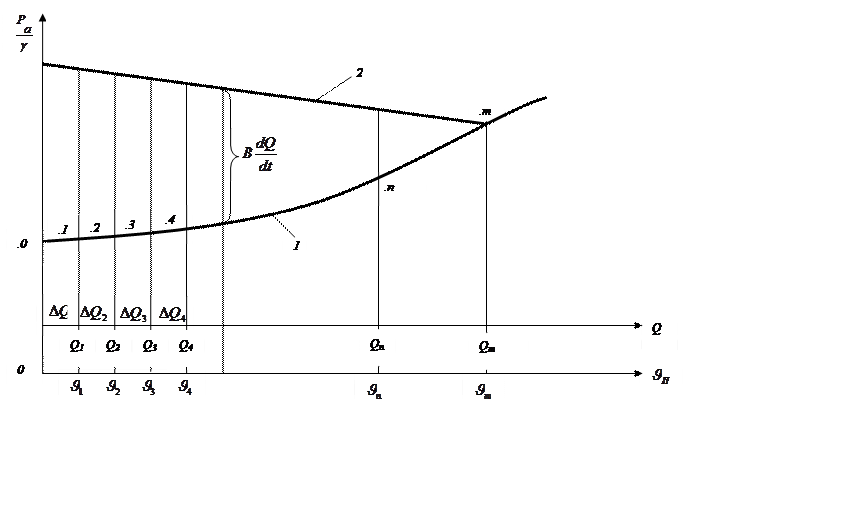
Точка пересечений линий I и 2 (точка m) соответствует установившемуся режиму работы гидросистемы, когда расход становится равным подаче насоса Q_m, а поршень движется с постоянной скоростью . Но этому режиму предшествует разгонный переходной режим, продолжительность которого нужно определить.

В начальный момент времени t=0, когда переключение гидрораспределителя уже сделано, поршень еще не подвижен , и потери напора в гидросистеме равны нулю:

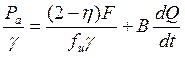                                                       (25)

Состояние системы при t=0 , на графике (рис.4) изображается точкой 0. Из графика, как разность ординат кривых 2 и I при Q=0, находим:

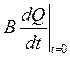, а затем определяем .

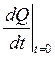Далее принимаем, что в течении небольшого промежутка времени  величина производной  постоянна.

Таким образом, подача жидкости в гидроцилиндр через промежуток времени  будет равен:

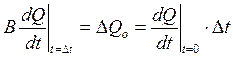                                        (26)

Соответственно, скорость поршня:

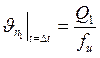.                                                   (27)

Расход  откладываем на графике (рисунок 4) и получаем точку I , которая определяет новое численное значение членов уравнения (24). Как разности ординат кривых 2и I при Q=Q₁ находим 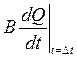и определяем 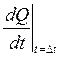.9

Далее снова принимаем, что в течении следующего промежутка времени [] величина производной 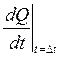не изменяется и определяем приращение расхода в течение этого промежутка времени

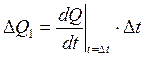                                             (28)

Соответственно подача жидкости в гидроцилиндр в момент времени :

                                                 (29)

и скорость поршня в момент времени :

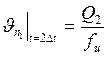                                                   (30)

Расход Q₂ откладываем на графике и получаем точку 2.

В точке 2 находим  в момент времени .

Таким образом приращение расхода в течение промежутка времени [] будет равно:

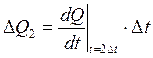                                           (31)

а расход в момент времени :

                                                 (32)

Соответственно, скорость поршня:

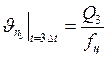                                                   (33)

и так далее.

Член выражающий потери AQ²  все время возрастает, т.к. растет расход. Величина инерционного напора (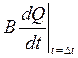) соответственно уменьшается; т. к. ускорение жидкости и поршня с грузом уменьшается; их скорость к стационарным значениям. Параллельно с построением на графике изменение расхода Q и скорости поршня  производится подсчет пути S, пройденного поршнем:

                                                   (34)

где

 ; ;…                                (35)