База завдань для підготовки до ректорського контролю з дисципліни "Математика" (з відповідями)

Б А З А   З А В Д А Н Ь

для підготовки до ректорського контролю з математики

ЛІНІЙНА АЛГЕБРА

1. Обчислити визначник 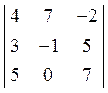. Відовідь: .

2. Обчислити визначник 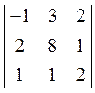. Відовідь: .

3. Обчислити визначник 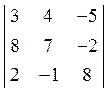. Відовідь: .

4. Обчислити визначник 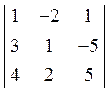. Відовідь: .

5. Обчислити визначник 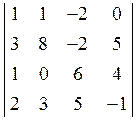. Відовідь: .

6. Обчислити визначник 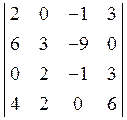 . Відовідь:  .

7. Обчислити визначник 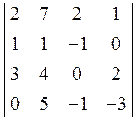 . Відовідь: . 

8. Обчислити визначник 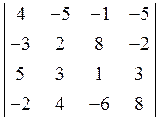 . Відовідь:  .

9. Обчислити визначник 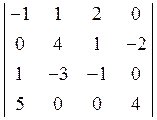 . Відовідь:  .

10. Дано: 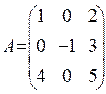, 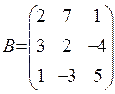.Знайти . Відовідь:  .

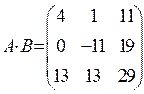11. Дано: 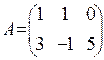, 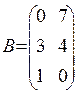.Знайти . Відовідь:  .

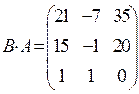12. Для даної матриці  знайти матрицю :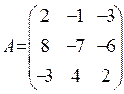.  Відовідь: .

13. Для даної матриці  знайти матрицю :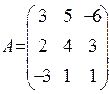. Відовідь: .

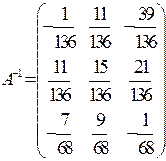14. Для даної матриці  знайти матрицю :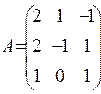. Відовідь: .

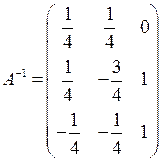15. Для даної матриці  знайти матрицю: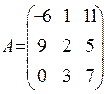. Відовідь:.

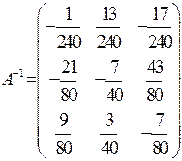16. Розв’язати систему лінійних рівнянь 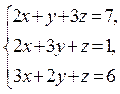 методом Гаусса. Відовідь: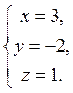

17. Розв’язати систему лінійних рівнян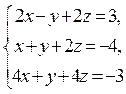ь методом Гаусса. Відовідь: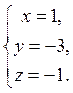

18. Розв’язати систему лінійних рівнян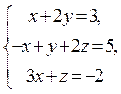ь  методом Гаусса. Відовідь: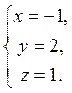

19. Розв’язати систему лінійних рівнянь 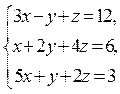 методом оберненої матриці.

      Відовідь:.

20. Розв’язати систему лінійних рівнянь 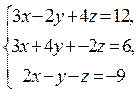 методом оберненої матриці.

      Відовідь:.

21. Розв’язати систему лінійних рівнянь 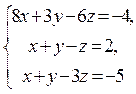 методом оберненої матриці.

      Відовідь:.

22. Розв’язати систему лінійних рівнянь 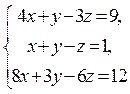 за формулами Крамера.

      Відовідь:.

23. Розв’язати систему лінійних рівнянь 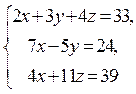 за формулами Крамера.

      Відовідь:.

24. Розв’язати систему лінійних рівнянь 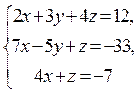 за формулами Крамера.

      Відовідь:.

25. Знайти ранг матриці 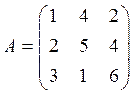. Відовідь: .

26. Знайти ранг матриці 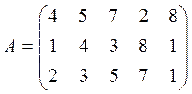. Відовідь: .

27. Знайти ранг матриці 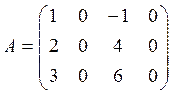. Відовідь:.

ВЕКТОРНА АЛГЕБРА

1.  За координатами точок , ,  для векторів

,  та відрізка  знайти: а) довжину вектора ; б) скалярний добуток векторів  і ; в) координати точки , яка ділить відрізок

 у відношенні . Відовідь: а); б); в) .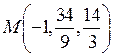

2.  За координатами точок , ,  для векторів

,  та відрізка  знайти: а) довжину вектора ; б) скалярний добуток векторів  і ; в) координати точки , яка ділить відрізок

 у відношенні . Відовідь: а); б) ; в).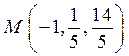

3.  За координатами точок , ,  для векторів

,  та відрізка  знайти: а) довжину вектора ; б) скалярний добуток векторів  і ; в) координати точки , яка ділить відрізок

 у відношенні . Відовідь: а); б) ;в) .

4.  За координатами точок , ,  для векторів

,  та відрізка  знайти: а) довжину вектора ; б) скалярний добуток векторів  і ; в) координати точки , яка ділить відрізок

 у відношенні . Відовідь: а) ; б); в) .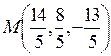

5.  Точки, , ,  є вершинами піраміди .

Знайти: а) площу грані ; б) об’єм піраміди . Відовідь: а); б) .

.

6.  Точки, , ,  є вершинами піраміди .

Знайти: а) площу грані ; б) об’єм піраміди . Відовідь: а) ; б) .

7.  Точки, , ,  є вершинами піраміди.

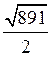Знайти: а) площу грані ; б) об’єм піраміди . Відовідь: а) ; б) .

8.  Точки, , ,  є вершинами піраміди .

Знайти: а) площу грані ; б) об’єм піраміди . Відовідь: а); б) .

АНАЛІТИЧНА ГЕОМЕТРІЯ

1.  Знайти рівняння прямої, що проходить через точку перетину прямих   та

 і відсікає на осі абсцис відрізок, рівний . Відовідь: .

2.   Знайти проекцію точки  на пряму, що проходить через точки  і

. Відовідь: .

3.  Дано дві вершини трикутника: та  і точка  перетину

його висот. Знайти координати вершини . Відовідь: .

4.  Знайти рівняння прямої, що відсікає на осі ординат відрізок, рівний , і паралельна до прямої . Відовідь: .

5.  Знайти відстань від точки  до площини, що проходить через точки

, , . Відовідь: .

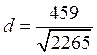6.  Обчислити відстань від точки  до площини, що проходить через точки

, , . Відовідь: .

7.  Знайти відстань від точки  до площини, що проходить через точки

, , . Відовідь: .

8.  Знайти відстань від точки  до площини, що проходить через точки

, , . Відовідь: .

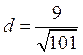9.  Знайти канонічні рівняння прямої, що задана як лінія перетину двох площин:

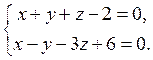 Відовідь: .

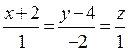10.  Знайти канонічні рівняння прямої, що задана як лінія перетину двох площин:

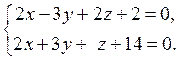 Відовідь: .

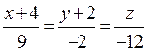11. Знайти канонічні рівняння прямої, що задана як лінія перетину двох площин:

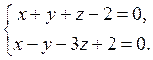 Відовідь: .

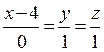12.  Знайти канонічні рівняння прямої, що задана як лінія перетину двох площин:

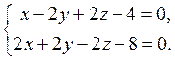 Відовідь: .

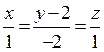13.  Знайти  канонічне рівняння еліпса, велика піввісь якого дорівнює , а фокус знаходиться в точці . Відовідь: .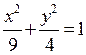

14.  Знайти  канонічне рівняння гіперболи, уявна піввісь якої дорівнює , а фокус знаходиться в точці . Відовідь: .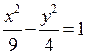

15.  Знайти канонічне рівняння параболи, якщо рівняння її директриси має вигляд

. Відовідь: .    

16.  Знайти рівняння  кола, що проходить через фокуси еліпса , і центр кола співпадає з верхньою вершиною еліпса. Відовідь: .

17. Знайти рівняння  прямої, що проходить через точки перетину двох кіл:

 і . Відовідь: .

18. Обчислити відстань від центра кола  до прямої, що проходить через точки перетину двох кіл: і . Відовідь: .

19. Знайти координати точки перетину прямої  і кола .

Відовідь: ,.

20. Знайти координати точки перетину прямої  і гіперболи .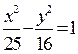

Відовідь: .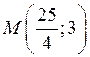

ГРАНИЦЯ ПОСЛІДОВНОСТІ

1. Довести, що .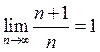

2. Довести, що .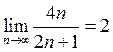

3. Довести, що .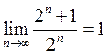

4. Довести, що .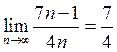

5. Знайти 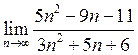. Відповідь:.

6. Знайти 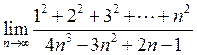. Відповідь: .

7. Знайти 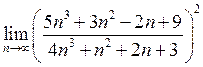. Відповідь: .

8. Знайти 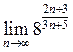. Відповідь: .

9. Знайти 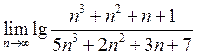. Відповідь: .

10. Знайти . Відповідь: .

11. Знайти . Відповідь: .

12. Знайти 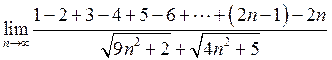. Відповідь: .

13. Знайти 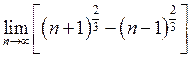. Відповідь: .

14. Знайти 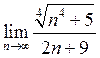. Відповідь: .

15. Знайти 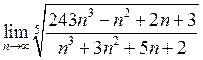. Відповідь: .

16. Знайти . Відповідь: .

17. Знайти 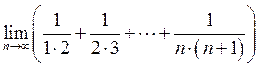. Відповідь: .

18. Знайти 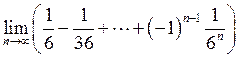. Відповідь: .

19. Знайти 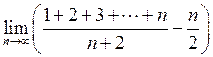. Відповідь: .

20. Знайти 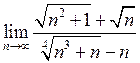. Відповідь: .

21. Знайти 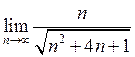.    Відповідь: .

22. Знайти 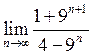.    Відповідь: .

23. Знайти 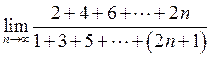. Відповідь: .

24. Знайти 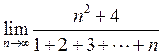. Відповідь: .

ГРАНИЦЯ ФУНКЦІЇ

1. Знайти 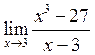. Відповідь: .

2. Знайти 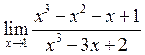. Відповідь: .

3. Знайти 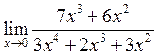. Відповідь: .

4. Знайти 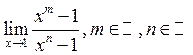. Відповідь: .

5. Знайти 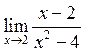. Відповідь: .

6. Знайти 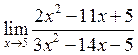. Відповідь: .

7. Знайти 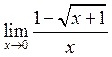. Відповідь: .

8. Знайти 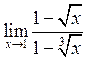. Відповідь: .

9. Знайти 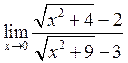.    Відповідь: .

10. Знайти 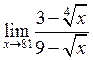.    Відповідь: .

11. Знайти 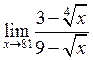.    Відповідь: .

12. Знайти 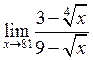.    Відповідь: .

13. Знайти 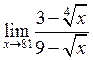.    Відповідь: .

14. Знайти 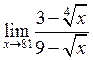.    Відповідь: .

15. Знайти 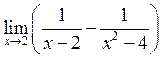.    Відповідь: .

16. Знайти 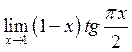.    Відповідь: .

17. Знайти 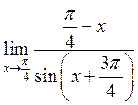.    Відповідь: .

18. Знайти .    Відповідь: .

19. Знайти 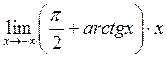.    Відповідь: .

20. Знайти 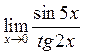.    Відповідь: .

21. Знайти 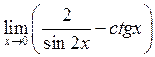.    Відповідь: .

22. Знайти 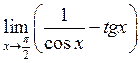.    Відповідь: .

23. Знайти 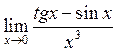.    Відповідь: .

24. Знайти 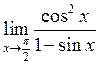.    Відповідь: .

25. Знайти 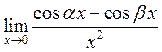.    Відповідь: .

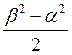26. Знайти 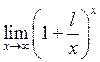.    Відповідь: .

27. Знайти .    Відповідь: .

28. Знайти 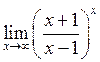.    Відповідь: .

29. Знайти 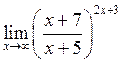.    Відповідь: .

30. Знайти 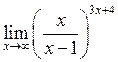.    Відповідь: .

31. Знайти 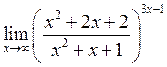.    Відповідь: .

32. Знайти 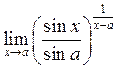.    Відповідь: .

33. Знайти 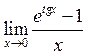.    Відповідь: .

34. Знайти .    Відповідь: .

35. Знайти 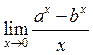.    Відповідь: .

36. Знайти 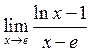.    Відповідь: .

37. Знайти порядок нескінченно малої  відносно нескінченно малої  при , якщо  і . Відповідь: .

38. Знайти порядок нескінченно малої  відносно нескінченно малої  при , якщо  і . Відповідь: .

39. Знайти порядок нескінченно малої  відносно нескінченно малої