Методичні вказівки до лабораторних робіт з навчальної дисципліни "Компресорні машини", страница 7

 або  .                                (2.6)

Витрачена потужність більше корисної на величину гідравлічних і механічних (тертя в підшипниках) втрат, її часто називають потужністю на валу вентилятора або підведеною.

У дослідах витрачену потужність визначають за показниками вимірювальних електроприладів, кВт:

, (2.7)

де  - ККД електродвигуна;   - сила струму, А;   - напруга, В.

ККД є відношення корисної потужності до витраченої

.                                                   (2.8)

Визначивши основні параметри вентилятора для різних продуктивностей, будують характеристику при сталій частоті обертання .

Результати спостережень і розрахунків зводяться в таблицях П.2.1  і  П.2.2.

На рис. 2.2. приведений зразок характеристики вентилятора при сталій частоті обертання.

3. Визначення характеристики мережі

Характеристика мережі служить для вибору машини, а також для визначення робочої точки К (рис.2.2), в якій машина працює при даних  , , , .

Мережею називаються елементи установки, що знаходяться перед і за вентилятором (всмоктувальні і нагнітальні патрубки, діафрагми, клапани та ін.), через які переміщується газ при роботі. В мережу входять також, наприклад, резервуар, в який попадає газ і та ін. Отже, мережа враховує корисні і шкідливі опори.

Таким чином, тиск у мережі   визначається величиною корисного тиску (тиску в резервуарі) і опором (втратами в ній). Задача вентилятора на кожному режимі   і   створити тиск  , рівний тиску в мережі, тобто завжди повинна виконуватися умова . Це означає, що характеристика мережі – залежність між витратою газу в мережі і величиною тиску, потрібного для забезпечення цієї витрати. Тому для вибору вентилятора (насоса, компресора) необхідно мати характеристику мережі  чи   частину її (розрахункові параметри).

Сполучення характеристики мережі з кривою тиску   визначає робочу точку К вентилятора на заданому режимі роботи його.

В даній установці основні втрати відбуваються у діафрагмі. Зневажаючи іншими втратами, можна визначити наближену характеристику мережі.

З рівняння Бернуллі і витрат, записаних для перерізів (2 -2) і (3-3),

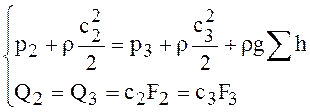,                                    (2.9)

де - втрачений напір, отримуємо рівняння для характеристики мережі

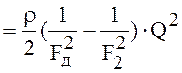, чи                                                        ,                                              (2.10)

де 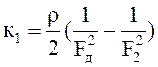  - стала величина для кожної діафрагми.

Отже, крива характеристики мережі є парабола, що виходить з початку координат (, ), тому що корисного опору немає.

При постійній частоті обертання і одній діафрагмі   може бути визначена тільки одна точка характеристики. Для розрахунку інших точок необхідно змінити частоту обертання вентилятора .

У дослідах частота обертання не змінюється, а так як витрата пропорційна частоті обертання в першому степені, то, задаючись декількома величинами витрати, можна визначити декілька точок характеристики мережі (табл. П.2.3).

4. Визначення характеристики при різній частоті обертання n=var

Ця характеристика представляє ряд кривих:

           і          ,

що звичайно визначаються за даними дослідів при різних частотах обертання, і є  найголовнішою для експлуатації машини. Однак у багатьох випадках з достатньою для практики точністю при зміні частоти обертання, приблизно, в межах n=(0,75...1,25)n_p, (n_p - розрахункова частота обертання) характеристика може бути визначена розрахунковим шляхом за даними характеристики при сталій  частоті обертання з використанням законів пропорціональності подібних машин:

 

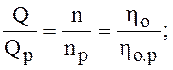
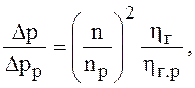
де  - об’ємний ККД;  - гідравлічний ККД.

В основі такого розрахунку лежить припущення, що при роботі з даною діафрагмою зі зміною частоти обертання режими залишаються подібними (трикутники швидкостей залишаються подібними). Тоді основні параметри вентилятора можуть бути перераховані за формулами:

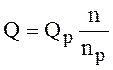     і 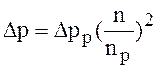       .                              (2.11)

Взагалі, подібність буде порушуватися за рахунок зміни ККД і тим значніше, чим більше робоча частота обертання буде віддалятися від розрахункової. Зауважимо, що з формул (2.6) і (2.11) випливає:

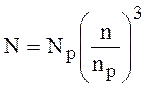.                                                       (2.12)