Математическая модель гидропривода с гидромотором

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ  ГИДРОПРИВОДА С  ГИДРОМОТОРОМ

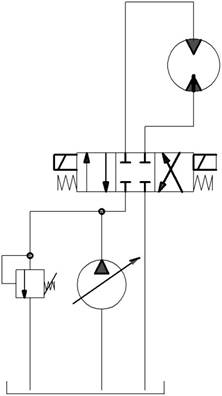
Расчётная схема гидропривода с гидромотором  изображена на рис. 1.

       При построении математической модели предполагается:

- момент сопротивления движению - постоянный;

- изменение момента инерции вращающихся масс не учитывать;

- давление слива на выходе гидромотора постоянно;

- волновые процессы в трубопроводах не учитывать ввиду незначительной протяженности;

- механический и гидравлический КПД - постоянны, равные средним значениям;

Геометрическая подача насоса без утечек рабочей жидкости

где характерный объем насоса (;

номинальная частота вращения вала насоса (;

Объем рабочей жидкости в отдающей полости насоса, равный  0,5

где рабочий объем насоса (;

Геометрический потребный расход гидромотора:

где  характерный объем мотора (

номинальная частота вращения вала мотора (

Модуль объемной упругости рабочей жидкости:

;

Коэффициенты перетечек насоса и мотора:

Коэффициенты полезного действия гидромотора:

механический,  гидравлический;

Коэффициент жидкостного трения:

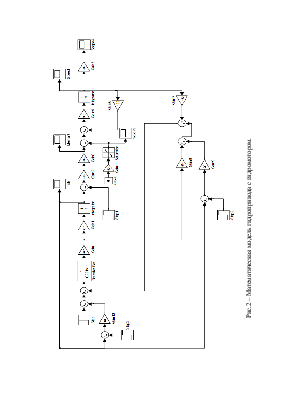
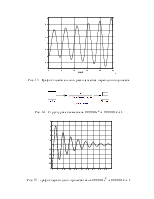
Пользуясь программой MATLAB Simulink собираю математическую модель гидропривода с гидромотором (рис. 2) и получаю графики переходных процессов.

В схеме имеется два интегратора, что указывает на второй порядок дифференциального уравнения, описывающего динамику рассматриваемой системы. Блок Transfer Fcn служит для исключения алгебраической петли. Петля вызвана тем, что на вход вычислительной схемы подается давление, которое потом вычисляется в схеме. Блоки Scope нужны для графического вывода переходных процессов. При исследовании системы в режиме разгона принимаю следующие начальные условия:0)=0,1МПа (атмосферное давление),  (гидропривод стоит). Эти начальные условия записываю в блоки интеграторов.

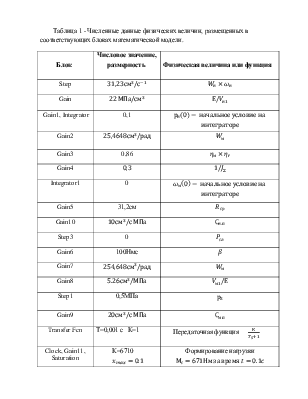
Числовые значения параметров гидропривода, их размерности, физическая сущность приведены в табл. 1.

Остальные блоки выполняют операции сложения, вычитания и деления.

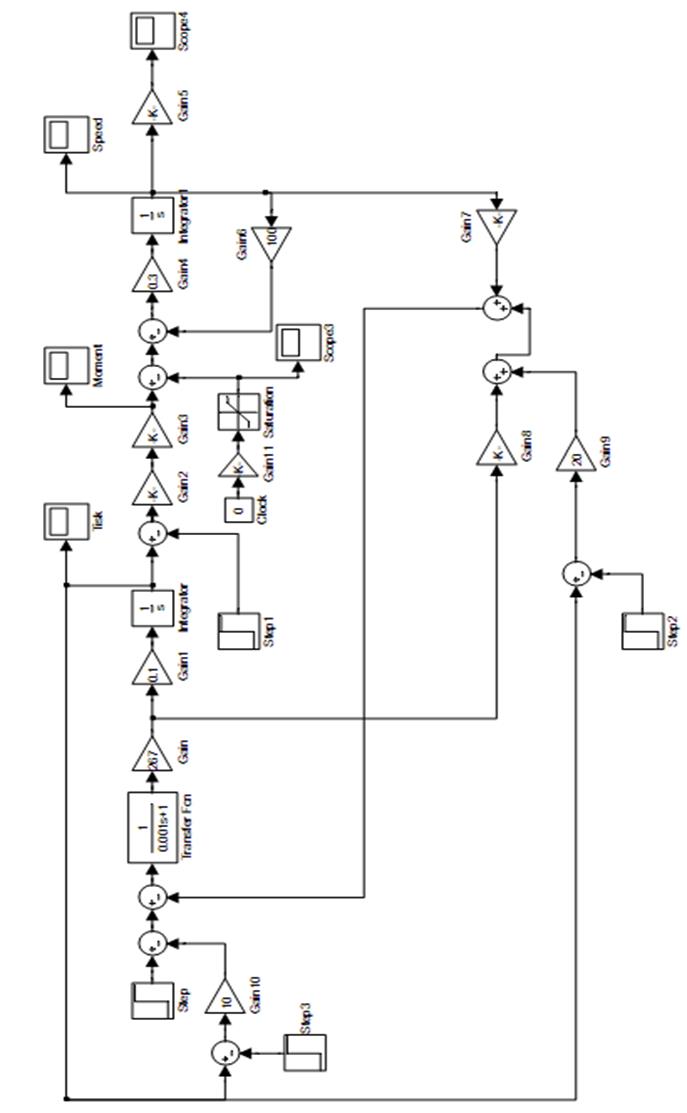
Таблица 1 - Численные данные физических величин, размещенных в  соответствующих блоках математической модели.     

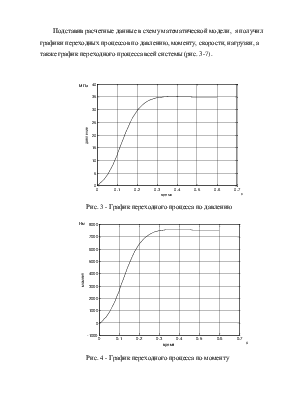
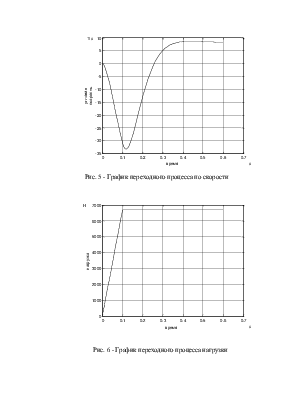
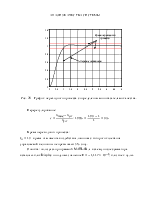
Подставив расчетные данные в схему математической модели,  я получил графики переходных процессов по давлению, моменту, скорости, нагрузки, а также график переходного процесса всей системы (рис. 3-7).              

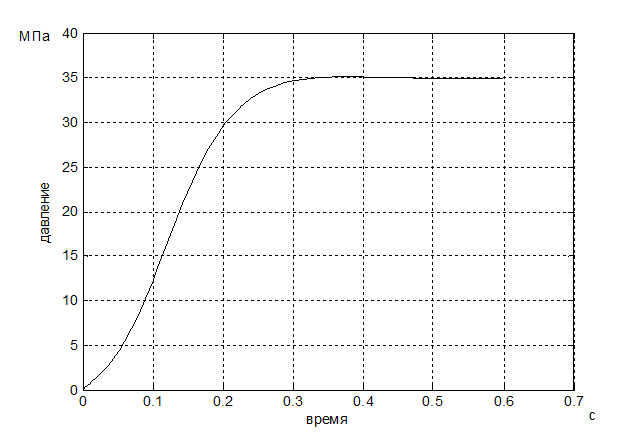
Рис. 3 - График переходного процесса по давлению

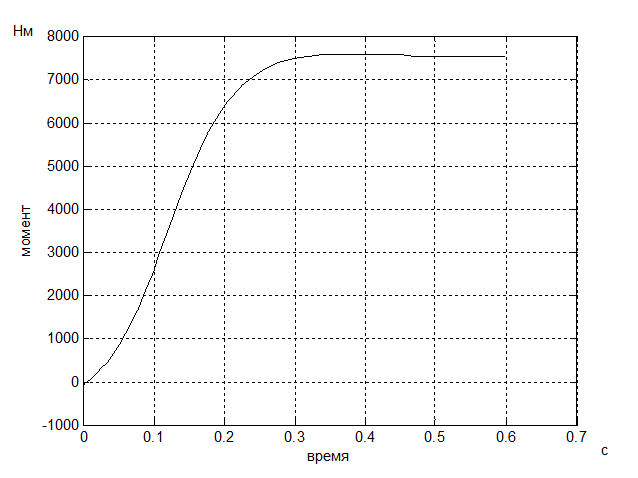
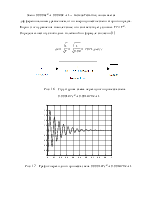
Рис. 4 - График переходного процесса по моменту

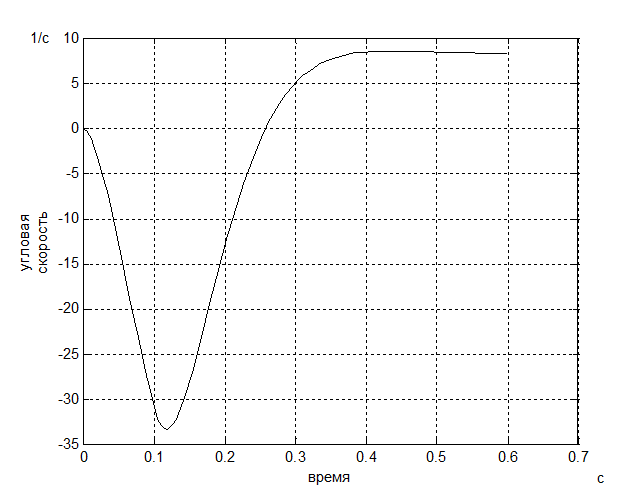
Рис. 5 - График переходного процесса по скорости

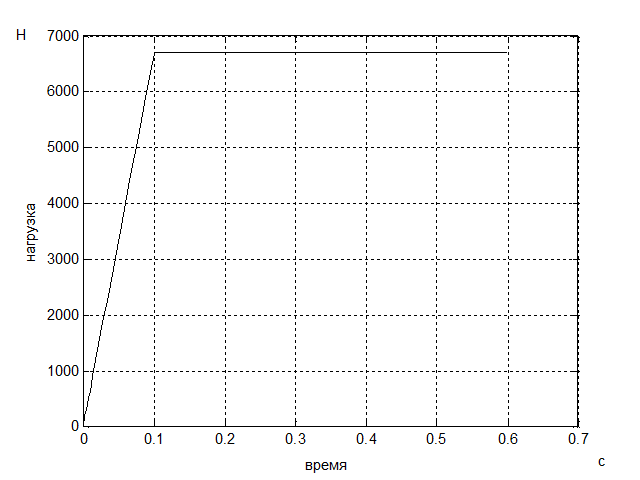
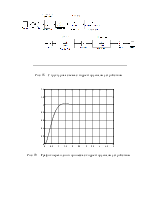
Рис. 6 - График переходного процесса нагрузки

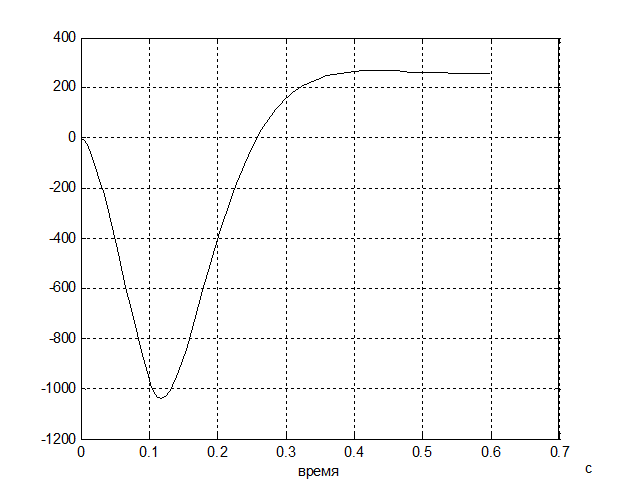
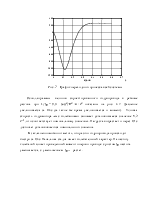
                Рис. 7 - График переходного процесса всей системы

Осциллограммы  величин спроектированного гидропривода в режиме разгона при =  показаны на рис. 3-7. Давление увеличивается за 0.3с (за такое же время увеличивается и момент).  Угловая скорость гидромотора  с колебаниями занимает установившееся значение 8,2 , что соответствует номинальному значению. Нагрузка возрастает и через 0,1с достигает установившегося номинального значения.

В заключении можно отметить, что разгон гидропривода происходит быстро за 0,3с. Начальная стадия имеет колебательный характер. На частоту колебаний влияет приведенный момент инерции привода: с ростом  частота уменьшается, с  уменьшением    растет.

Синтез корректирующего устройства

В выражении для передаточной функции сервомеханизма «насос-гидромотор» используются следующие коэффициенты:

коэффициент передачи между ходом поршня электрогидравлического сервомеханизма и перемещением управляющего органа насоса

коэффициент усиления насоса по расходу

коэффициент усиления сервомеханизма «насос-гидромотор» по скорости

коэффициент усиления сервомеханизма «насос-гидромотор» по моменту

Согласно[2] резонансная частота определяется по формуле

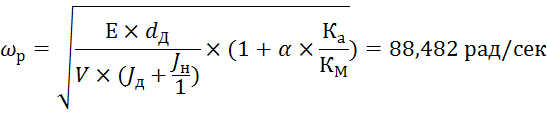
где     модуль объемной упругости рабочей жидкости;

эффективный объем жидкости гидросистемы;

момент инерции гидродвигателя;

момент инерции нагрузки;

коэффициент вязкостного трения гидромотора и нагрузки, приведенный к валу гидромотора

Согласно [2] коэффициент демпфирования определяется по формуле

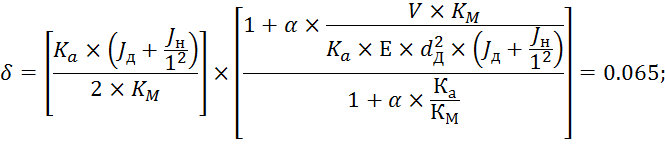
Согласно[ 2] система гидропривода с гидромотором описывается передаточной           функцией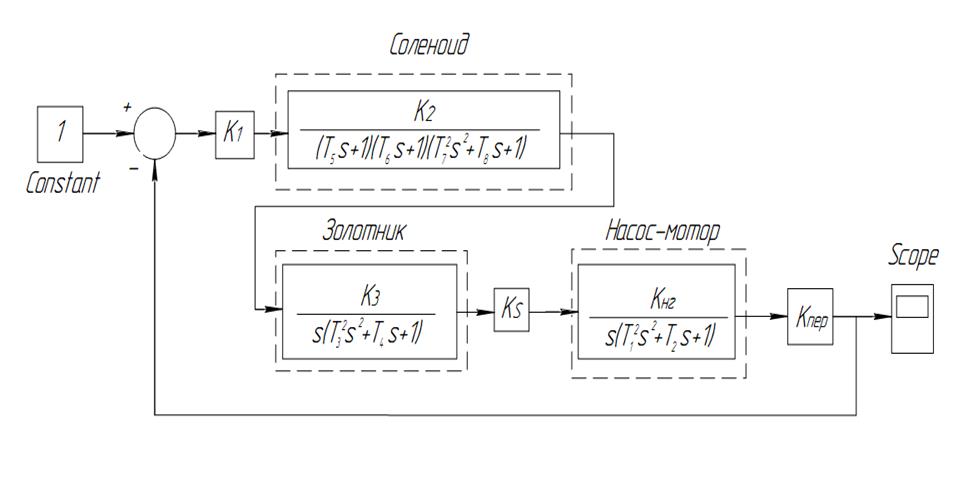

Рис. 8 – Структурная схема  передаточной функции «насос-гидромотор»

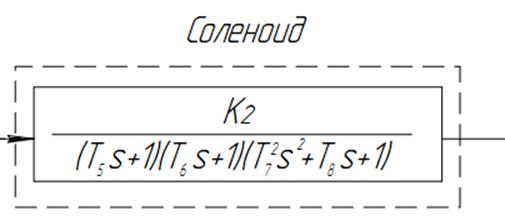
Согласно [2] соленоид описывается передаточной функцией, в которой