Математическая модель гидропривода с гидромотором, страница 2

Рис. 9 -  Схема передаточной функции соленоида

Т5=0,02;T6=0,007;T7=0,02; T8=0,0028; К2=0,8; золотник (рис.10)  и насос-мотор (рис.11) в которых соответственно T3=0,000127; T4=0,001479; КЗ=10,1 и T1=0,000127;T2=0,001479;

КНГ=1].  Пользуясь программой MATLAB Simulink собираю структурную схему (рис.12) и получаю график переходного процесса (рис.13).

Рис. 10 – Схема передаточной функции золотника

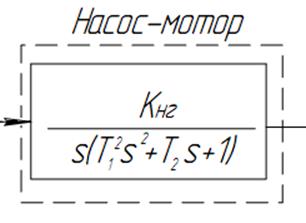
Рис.11 – Схема передаточной функции системы «насос-мотор»

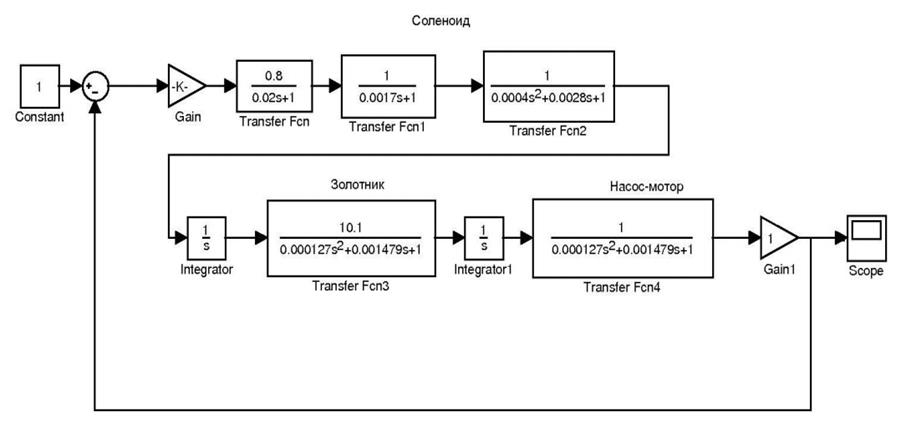
Рис. 12 - Структурная схема переходного процесса

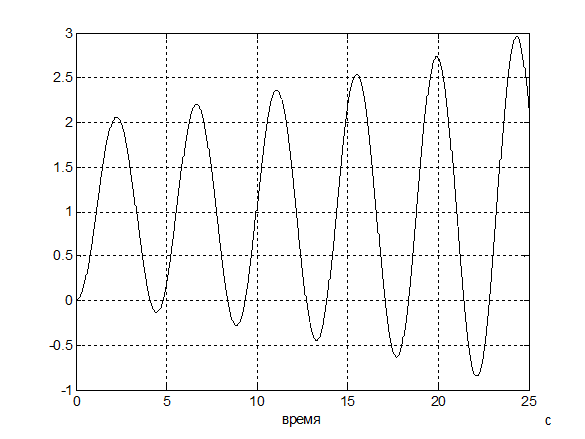
Рис. 13 – График колебательного расходящегося переходного процесса

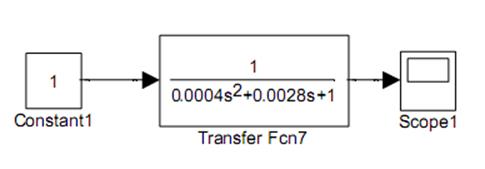
Рис. 14 – Структурная схема звена

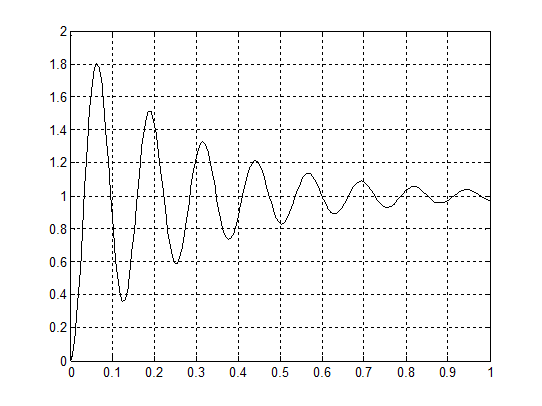
Рис. 15 – график переходного процесса звена

Звено  описывается дифференциальным уравнением, что и апериодическое звено второго порядка.  Корни этого уравнения комплексные, что соответствует условию  Определяю частоту свободных колебаний по формуле согласно [1]   

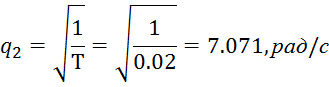
               Рис. 16 – Структурная схема переходного процесса звена

 

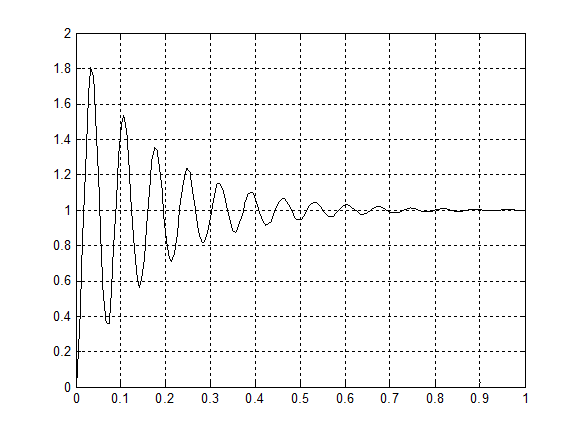
Рис. 17 – График переходного процесса звена          

Звено  описывается дифференциальным уравнением, что и апериодическое звено второго порядка.  Корни этого уравнения комплексные, что соответствует условию  Определяю частоту свободных колебаний по формуле согласно[1]   

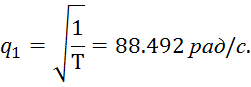
Определяю сопрягающие частоты по формуле согласно [1]

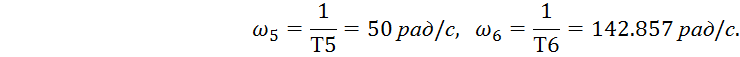
Прологарифмируем  их

Определяем коэффициент передачи 

.

Для построения Л.А.Х. находится величина Lo(отмечаю точку на Л.А.Х. приложение 1)   

Построение располагаемой Л.А.Х. начинаю из точки Lo, провожу прямую под углом -40дб/дек, т.к. в схеме имеется два интегратора до первой частоты (в данном случае ). Увеличиваю угол наклона на -40дб/дек и провожу линию до частоты. Т5 в первой степени, поэтому увеличиваю угол наклона еще на -20дб/дек и провожу линию до частоты . Увеличиваю угол наклона еще на -80дб/дек и провожу линию до частоты  Т6 в первой степени, значит увеличиваю угол наклона еще на -20дб/дек.                                                                                                 

При построении желаемой характеристики необходимо чтобы порядок передаточной функции был не ниже порядка разомкнутой системы. Задаюсь параметрами tp=3с – время регулирования,  - перерегулирование. Определяю  согласно [1] рис.12.3  по формуле

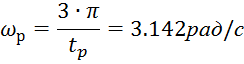
Далее по найденной частоте положительности  определяю частоту среза Л.А.Х. так, чтобы она удовлетворяло условию согласно [1]

Прологарифмируем :

  (отмечаю точку на Л.А.Х. приложение 1)

Построение желаемой Л.А.Х. начинаю из точки , через которую провожу прямую под наклоном  -20дб/дек. Среднечастотный участок образованный асимптотой с наклоном -20дб/дек служит для обеспечения устойчивости, и для обеспечения заданных показателей качества. Этот участок проводится влево и вправо до достижения модулей, равных  Затем произвожу сопряжение среднечастотного участка с низкочастотными асимптотами и высокочастотной частью.  

    Если желаемая передаточная функция разомкнутой системы ,  - располагаемая и передаточная функция корректирующего устройства последовательного типа  , то можно записать равенство согласно [1]

отсюда

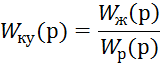
Для Л.А.Х. можно записать согласно[1] из ординат желаемой Л.А.Х. вычитаю ординаты располагаемой Л.А.Х.  Получившаяся Л.А.Х. соответствует передаточной функции последовательного корректирующего звена.

В качестве корректирующего устройства использую дифференцирующее звено первого порядка  .

Вставляю корректирующее устройство в схему (рис. 18) и получаю график сходящегося переходного процесса.

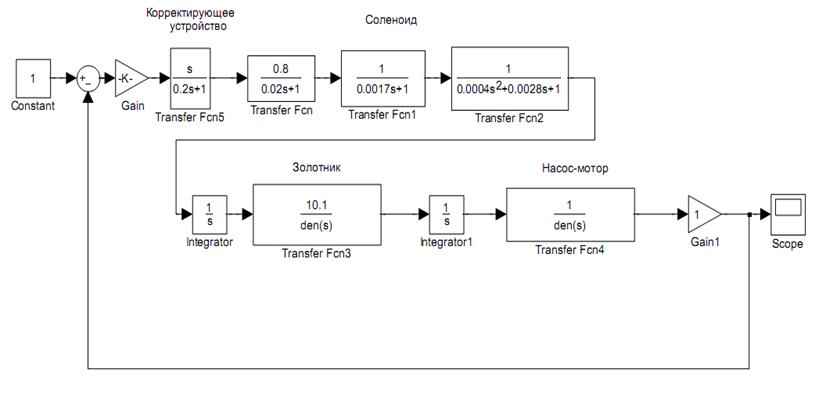Рис. 18 – Структурная схема с корректирующим устройством

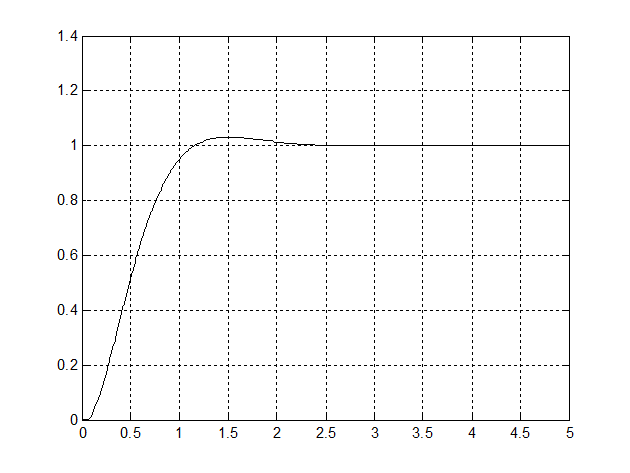
Рис. 19 -  График переходного процесса с корректирующим устройством

АНАЛИЗ КАЧЕСТВА СИСТЕМЫ

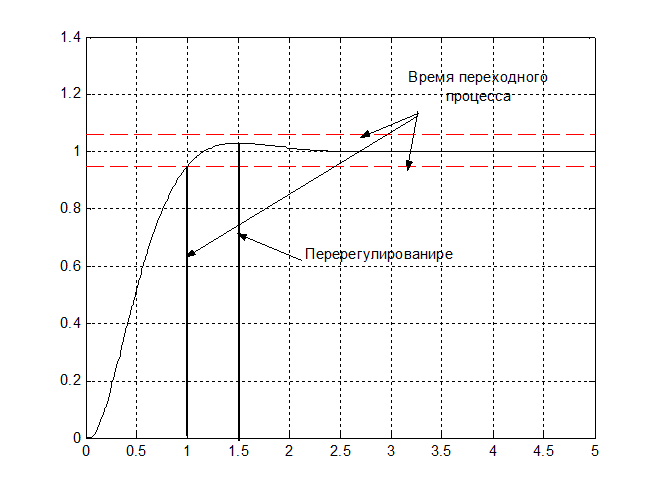
Рис. 20 – График переходного процесса с определенными показателями качества.

Перерегулирование:

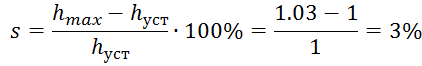
Время переходного процесса:

 – время от момента воздействия, начиная с которого колебания управляемой величины не превышают 5% зону.

Ошибка: пользуясь программой MATLAB, я в схему после сумматора вставляю блок Display и получаю значение , близкое к нулю.

Выводы: я освоил методику расчета динамики гидропривода с гидромотором, составления  математической модели системы и реализации её в программе MATLAB, расчета последовательного корректирующего устройства методом ЛАЧХ (график переходного процесса стал устойчивым) и анализа показателей качества системы (время переходного процесса 1с, перерегулирование 3%, хотя задавались значением 15%, уложились в заданный параметр, что неплохо, ошибка    - число близкое к нулю, т.к. в системе имеются интегрирующие звенья, которые входят в общую передаточную функцию, значит, что установившееся ошибка равна 0. Системы, у которых статическая ошибка равна 0 называются астатическими.

Перечень ссылок

1. Бесекерский В.А. Теория систем автоматического управления. Изд. 4-е перераб. и  доп.- СПб. Изд. «Профессия».- 2003г.-752с.

2. Гидравлические системы управления / Э. Льюис, Х. Стерн ; пер. с англ. А. М. Банштыка, А. М. Плунгяна ; под ред. И. М. Крассова. - М.: Мир, 1966. - 407 с.: ил. - Библиогр.: с. 385

3.  Финкельштейн  З.Л.  Применение  и  очистка  рабочих жидкостей для горных машин. – М.: Недра, 1986. – 232с.

4. Башта  Т.М.  Объемные  гидравлические  приводы.  –  М.: Машиностроение, 1968. – 628с

5. Финкельштейн  З.Л. Расчет, проектирование и эксплуатация объемного гидропривода: Учеб. пособие – 2006.-216с.