Построение проекций отрезка прямой линии. Определение истинной величины отрезка

Санкт-Петербургский государственный морской технический университет

Кафедра компьютерной графики и информационного обеспечения

ЗАНЯТИЕ 2

1.  Отрезок прямой линии.

Построение проекций отрезка прямой линии.

Форму любого геометрического объекта определяет совокупность точек, связанных между собой отрезками прямой линии.  Для того чтобы построить проекции отрезка, достаточно построить проекции двух точек – начала и конца, и соединить их. В теории начертательной геометрии отрезок рассматривается как элемент сложных конструкций.

 Основными характеристиками отрезка являются его действительная (истинная) величина и углы его наклона к плоскостям проекций.

Определение истинной величины отрезка и углов его наклона к плоскостям проекций.

Истинная величина отрезка. Если отрезок в пространстве занимает общее положение, т.е. если он не параллелен  никакой из плоскостей проекций, то проекции такого отрезка всегда меньше, чем сам отрезок в пространстве. Работая с плоской моделью отрезка, важно уметь находить его истинную величину. Для этого используются следующие методы:

1)  метод прямоугольного треугольника;

2)  метод перемены плоскостей проекций;

3)  метод вращения.

Углы отрезка. В качестве угла между отрезком и плоскостью проекций принимается угол между отрезком и его проекцией на плоскость. Принятое обозначение углов:

φ  - угол наклона к горизонтальной плоскости  проекций П1;

ψ – угол наклона к фронтальной плоскости проекций П2.

Величина этих углов определяется теми же методами, что  и истинная величина отрезка, причем, их определение неразрывно связано друг с другом.         

Определение истинной величины отрезка и углов его наклона к плоскостям проекций с использованием метода преобразования чертежа.

 Метод вращения вокруг оси, перпендикулярной к плоскости проекций. Построения этим методом целиком реализуются в начальной системе координат. Изменяется положение геометрического объекта. При этом главная цель – перевести объект из общего положения в частное, т.е когда отрезок параллелен к плоскости проекций.

Для того, чтобы осмысленно применять метод, необходимо  знать наборы частных положений геометрических объектов, которые позволяют легко достигать поставленных в задаче целей.

Основные принципы метода. Все построения выполняются в начальной системе координат и, следовательно, любой геометрический объект задается двумя проекциями – горизонтальной и фронтальной. Изменение положение объекта в пространстве неизбежно ведет и к изменению обеих  проекций. Это следующие изменения:

a)  изменения положения – обе проекции меняют его одновременно;

b)  изменения формы и размеров – одна проекция неизменна, а другая деформируется;

c)  траектория перемещения – точки одной проекции переходят в новое положение по дуге окружности, а второй по горизонтальным линиям, т.е. по линиям, параллельным оси Х.

Чтобы конкретизировать отмеченные свойства метода, необходимо выбрать ось вращения: пусть это будет ось, перпендикулярная к горизонтальной плоскости проекций П1_.  В этом случае:

a)  горизонтальная проекция переходит в новое положение неизменной по форме (как жесткая фигура), а траектория движения ее точек – дуга окружности;

b)  фронтальная проекция в новом положении имеет другую форму и размеры. Траектория движения точек – прямая линия.

Для получения поставленной в задаче цели, выбирается положение оси для первого вращения. Допустим, выбрана ось, перпендикулярная к П1_. Как правило, нужное частное положение достигается за одно или два преобразования и, если нужно делать второе вращение, то вторая ось должна быть перпендикулярна к другой плоскости, а именно к П2 в данном случае. Тогда

a)   фронтальная проекция переходит в новое положение неизменной по форме (как жесткая фигура), а траектория движения ее точек – дуга окружности;

b)  горизонтальная проекция в новом положении имеет другую форму и размеры. Траектория движения точек – прямая линия.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ №2

Определение истинной величины отрезка.

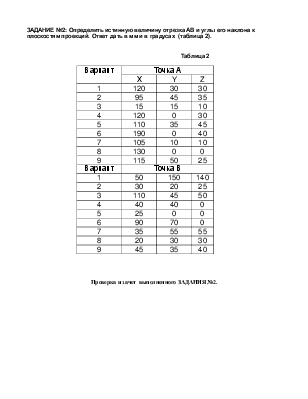
Начальное условие тестового примера (выполняется на практическом занятии) -  координаты двух точек отрезка: В(40; 10; 55);       А165; 95; 110) (см. рис.1).

Задание и построение начального условия аналогичны  рассмотренным выше в практическом задании №1. Сделать текущим слой СО и, используя команду Отрезок (Line), соединить между собой проекции А1В1 и А2В2

Текущий слой ТМР. Используя команду Отрезок (Line)  обвести проекции А1В1 и А2В2. Слой СО заблокировать, для чего в списке управления слоями закрыть замок. Это надо сделать по той причине, что при использовании команды Повернуть (Rotate), надо сохранить на экране начальное условие.

          Падающее меню Изменить-Повернуть (Modify – Rotate). Указать курсором объект для поворота (запрос в командной строке Selectobjects:) – проекцию А1В1 в слое ТМР. Отрезок выделится пунктиром. Команда повторяет запрос объекта, но так как надо вращать один объект, то нажать кнопку  ввода Enter на клавиатуре. В командной строке появится запрос базовой точки (Specifybasepoint:), вокруг которой будет производиться вращение – указать курсором на точку А1 и дождаться подсказки на экране – Конечная точка (Endpoint). Возможны подсказки другого содержания, что не так важно, как само появление подсказки, свидетельствующее о том, что система точно поймала точку.

          Отключить режим ОРТО (ORTHO), если он включен и, перемещая мышь, поместить отрезок А1В1 в строго горизонтальное положение. В результате получена проекция А1*В1*по форме и размеру равная проекции А1В1 и расположенная параллельно оси Х. Заблокировать слой ТМР, слой СО разблокировать (открыть замок). Команда Отрезок (Line) – обвести проекцию А1*В1*.

 Такое расположение горизонтальной проекции соответствует положению пространственного отрезка АВ параллельно фронтальной плоскости проекций П2. Значит на плоскость П2 отрезок проецируется без искажения, т.е. А2*В2* = АВ. Строим новую фронтальную проекцию. Точка А неподвижна, так как через нее проходит ось вращения: точка А2* будет совпадать с точкой А2  и А1* совпадаетс А1.

Включить режим ОРТО (ORTHO) и сделать текущим слой ТМР. Для того, чтобы получить точку В2* надо из точки В2  провести горизонтальную линию, а из точки В1* вертикальную. Точка пересечения этих линий даст положение новой проекции В2*. Сделать текущим слой СО и соединить А2* с точкой В2*. Получено  частное положение, при котором   определяется истинная величина отрезка.

Определение угла φ. В полученном положении угол между фронтальной проекцией А2*В2* и осью X равен углу φ.

Определение угла ψ. Для определения этого угла методом вращения, необходимо получить частное положение, при котором отрезок становится параллельным горизонтальной плоскости проекций. На чертеже это определяется тем, что фронтальная проекция располагается параллельно оси X, т.е. нужно повернуть проекцию А2В2 вокруг оси, перпендикулярной к П2.

Строгое использование метода вращения, которое было применено для вращения горизонтальной проекции, часто приводит к наложению новых проекций на старые или к излишним взаимным пересечениям линий. Однако, указанное выше свойство неизменности проекции на ту плоскость, к которой перпендикулярна ось вращения, позволяет выполнять построения так, чтобы не было наложений.

Этот вид реализации метода вращения получил название метод плоскопараллельного переноса.      В его основе лежит следующее: неизменную по форме и размерам проекцию можно перенести на удобное свободное место и только потом повернуть ее в нужное положение. Вторая проекция строится так же, как и в случае строгой реализации метода вращения. Используем это.

Падающее меню Изменить-Копировать (Modify – Copy). Курсором указать объект для копирования проекцию А2В2 (на слое ТМР). Указать базовую точку для копирования – точку В2. Указать вторую точку для копирования, т.е. ту точку, в которую надо перенести точку В2  - это любая точка на свободном пространстве и ей присваивается обозначение В2**. Команда Повернуть (Rotate) – повернуть скопированный отрезок вокруг точки В2** до горизонтального положения: получена проекция А2** В2**.

                      

Рис.1. Определение истинной величины и углов наклона отрезка методом вращения.

Далее из точки А1 строится горизонтальная линия, а из точки А2** вертикальная – точка их пересечения даст проекцию А1**.  Аналогично строится проекция В1**. Строятся проекции А1** В1**  и А2** В2**.

В результате А1**В1**  = АВ и угол между А1**В1**  и осью X есть угол наклона отрезка АВ к фронтальной плоскости проекций ψ. Результат рассмотренных построений показан на рис.1.

ЗАДАНИЕ №2: Определить истинную величину отрезка АВ и углы его наклона к плоскостям проекций. Ответ дать в мм и в градусах  (таблица 2).

                                                    Таблица 2 

Вариант	Точка А
	Х	Y	Z
1	120	30	30
2	95	45	35
3	15	15	10
4	120	0	30
5	110	35	45
6	190	0	40
7	105	10	10
8	130	0	0
9	115	50	25
Вариант	Точка В
1	50	150	140
2	30	20	25
3	110	45	50
4	40	40	0
5	25	0	0
6	90	70	0
7	35	55	55
8	20	30	30
9	45	35	40

Проверка и зачет  выполненного ЗАДАНИЯ №2.