Расчет фундаментов и металлической рамы здания (Расчетно-конструктивный раздел дипломного проекта)

2. Расчетно – конструктивный раздел

2.1. Расчет фундаментов

2.1.1. Компоновка конструктивной схемы

Фундамент имеет в плане прямоугольную форму, и коробчатое сечение. Каналы направлены перпендикулярно общей длине здания. Для расчета коробчатого сплошного фундамента вырезаем балку двутаврового профиля и рассчитываем ее. Поперечное сечение вырезанного участка фундамента изображено на рис. 2.1.

Поперечное сечение вырезанного участка фундамента

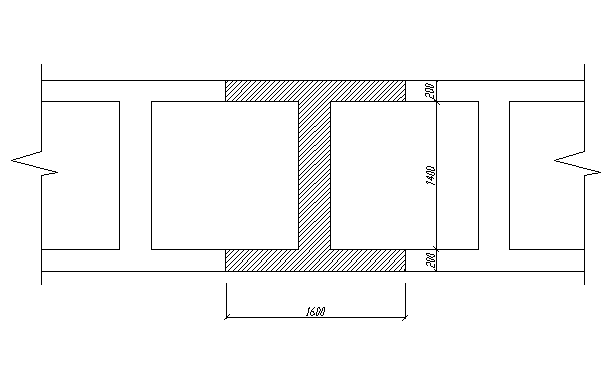Рис. 2.1

2.1.2. Сбор нагрузок

Для определения расчетной нагрузки на фундамент выполняем  сбор нагрузок. Сбор нагрузок ведем в табл.2.1.

Таблица 2.1

Сбор нагрузок на 1 м²

Конструкция покрытия	Нормативная нагрузка, кН/м2	Коэффициент надёжности по нагрузке, gf	Расчётная нагрузка, кН/м2
Постоянная нагрузка:
1. Ледовое поле с разводкой техно-логического трубопровода 120 мм.	0,27	1,3	0,35
2. Теплоизоляционный слой – пеноплекс – 100 мм.	0,1	1,3	0,13
3. Теплорегулирующий слой с разводкой технологического трубопровода - 80 мм	0,4	1,3	0,52
4. Теплоизоляция минераловатные плиты на синтетическом связующем - 150 мм	0,1	1,2	0,12
5. Пароизоляция – 2 слоя гидроизола на мастике	0,1	1,3	0,13
6. Монолитная ж/б плита	1,8	1,1	1,98
Временная нагрузка:
1. Нагрузка от льдоуборочной машины	0,5	1,1	0,55
2. Нагрузка от людей	0,08	1,1	0,088
Итого q0	3,36		3,87

2.1.3. Статический расчет   

Рассчитываем вырезанную часть фундамента (балку двутаврового сечения) как балку на упругом полупространстве. Этот метод предложен Б.Н. Жемочкиным и А.П. Синициным. Непрерывную связь между балкой и основанием в расчетной системе заменяют сосредоточенными абсолютно жесткими стержнями. Усилия в стержнях принимают равновеликими равнодействующей давления, равномерно распределенного по площади подошвы, соответствующей каждому стержню. Обычно расстояния между стержнями назначают одинаковыми, а число участков - равным 9 – 11. Такая статическая схема представлена на рис. 2.2.

Статическая схема и схема нагрузок

Рис. 2.2

Основную систему расчета можно получить (по смешанному методу расчета статически неопределимых систем), отделив балку от основания, заменив при этом действие стержней действием усилий Х₀, …, Х₇ и вводя заделку в середине балки. Неизвестным при этом оказываются усилия Х₀, …, Х₇ и осадка заделки у₀. Значения неизвестных находят из решения системы уравнений. Длину участков назначаем равную 2 метрам. Для облегчения расчетов используем симметрию балки и нагрузок. В этих целях по оси балки расположим заделку и разрежем все вертикальные стерженьки, заменив их неизвестными силами Х₀, …, Х₇ . Основная система для расчета изображена на рис. 2.3.

Основная система

Рис. 2.3

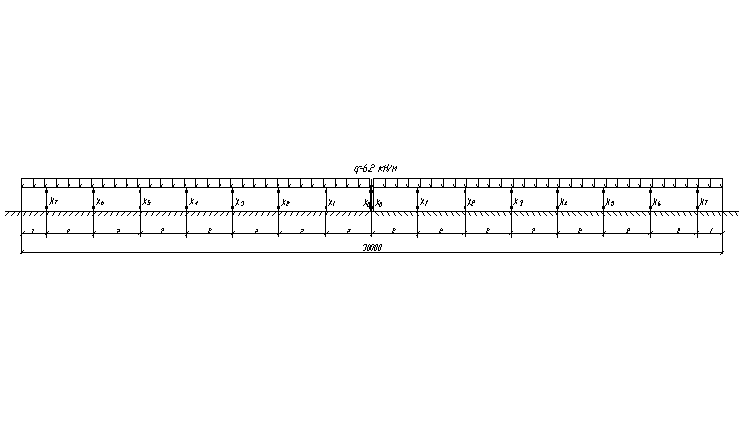
Для расчета подобных систем составляют обычные канонические уравнения, выражающие условия, что суммарные перемещения по направлению каждого разрезанного стерженька равны нулю. Указанные перемещения зависят от действия всех сил Х в опорных стерженьках, действия внешней нагрузки D_ip и от осадки y₀,  которую претерпевает балка в месте заделки.

Канонические уравнения будут иметь вид:

d₀₀Х₀ + d₀₁Х₁ + d₀₂Х₂ + d₀₃Х₃ + d₀₄Х₄ + d₀₅Х₅ + d₀₆Х₆ + d₀₇Х₇ – у₀ = 0;

d₁₀Х₀ + d₁₁Х₁ + d₁₂Х₂ + d₁₃Х₃ + d₁₄Х₄ + d₁₅Х₅ + d₁₆Х₆ + d₁₇Х₇ – у₀  + D_1p = 0;

d₂₀Х₀ + d₂₁Х₁ + d₂₂Х₂ + d₂₃Х₃ + d₂₄Х₄ + d₂₅Х₅ + d₂₆Х₆ + d₂₇Х₇ – у₀  + D_2p = 0;

d₃₀Х₀ + d₃₁Х₁ + d₃₂Х₂ + d₃₃Х₃ + d₃₄Х₄ + d₃₅Х₅ + d₃₆Х₆ + d₃₇Х₇ – у₀  + D_3p = 0;

d₄₀Х₀ + d₄₁Х₁ + d₄₂Х₂ + d₄₃Х₃ + d₄₄Х₄ + d₄₅Х₅ + d₄₆Х₆ + d₄₇Х₇ – у₀  + D_4p = 0;

d₅₀Х₀ + d₅₁Х₁ + d₅₂Х₂ + d₅₃Х₃ + d₅₄Х₄ + d₅₅Х₅ + d₅₆Х₆ + d₅₇Х₇ – у₀  + D_5p = 0;

d₆₀Х₀ + d₆₁Х₁ + d₆₂Х₂ + d₆₃Х₃ + d₆₄Х₄ + d₆₅Х₅ + d₆₆Х₆ + d₆₇Х₇ – у₀  + D_6p = 0;

d₇₀Х₀ + d₇₁Х₁ + d₇₂Х₂ + d₇₃Х₃ + d₇₄Х₄ + d₇₅Х₅ + d₇₆Х₆ + d₇₇Х₇ – у₀  + D_7p = 0.

Кроме того, необходимо использовать уравнение равновесия:

- Х₀ - Х₁ - Х₂ - Х₃ - Х₄ - Х₅ - Х₆ - Х₇ + SР = 0.

Таким образом, в нашем распоряжении оказывается 9 уравнений, содержащих 9 неизвестных Х₀, …, Х₇  и y₀.

При этом первые восемь уравнений выражают условия, что суммарные перемещения по направлению Х₀ , Х₁ , Х₂ , Х₃ , Х₄ , Х₅ , Х₆ и Х₇ равны нулю, последнее уравнение – равенство нулю суммы проекций всех сил на вертикальную ось.

Отсутствие в первом уравнении свободного члена D_0p объясняется тем, что внешняя нагрузка не вызывает перемещения по направлению силы Х₀, расположенной в месте заделки.

Перемещения d_ki входящие в канонические уравнения, состоят из перемещений у_ki от осадки основания и из прогиба балки v_ki, т.е.

d_ki = у_ki + v_ki.

В случае полупространства осадку определяют по формуле Буссинеску, на основании которой Б.Н. Жемочкин получил следующее выражение:

у_ki = (1 - m₀²)*F_ki  /  pE₀c, где у_ki – осадка в точке к от единичной силы, приложенной в точке i;

F_ki – некоторая функция, целиком зависящая от величины отношения b/c;

Единичные прогибы можно определять по выражению:

v_ki = с³  /  6Е_бI   *  v_ki;

Функция v_ki целиком зависит от значений аi и аk, соответственно равных расстоянию от условной заделки балки до точки i приложения сосредоточенной силы и от заделки балки до сечения ее к, где определяется прогиб.

Таким образом:

d_ki = (1 - m₀²) (F_ki ^‘ +av_ki) / (pE₀c), где a = (pE₀c⁴) / (6Е_бI*(1 - m₀²)).

a = (3,14*10000*2⁴) / ( 6*3,14*10⁶*0,085*(1 – 0,3²) = 0,312

Далее переходим к вычислению единичных перемещений, тогда как для b/c = 0,7, получим:

d₀₀ = 4,265 + 4,265 = 8,53

d₀₁ = 1,069 * 2 = 2,138

d₀₂ = 0,508 * 2 = 1,016

d₀₃ = 0,336 * 2 = 0,672

d₀₄ = 0,251 * 2 = 0,502

d₀₅ = 0,2 * 2 = 0,4

d₀₆ = 0,167 * 2 = 0,334

d₀₇ = 0,143 * 2 = 0,288

d₁₁ = 4,265 + 0,508 + 0,312 * 2 = 5,397

d₁₂ = 1,069 + 0,336 + 0,312 * 5 = 2,965

d₁₃ = 0,508 + 0,251 + 0,312 * 8 = 3,255

d₁₄ = 0,336 + 0,2 + 0,312 * 11 = 3,968

d₁₅ = 0,251 + 0,167 + 0,312 * 14 = 4,786

d₁₆ = 0,2 + 0,143 + 0,312 * 17 = 5,647

d₁₇ = 0,167 + 0,125 + 0,312 * 20 = 6,532

d₂₂ = 4,265 + 0,251 + 0,312 * 16 = 5,508

d₂₃ = 1,069 + 0,2 + 0,312 * 28 = 10,005

d₂₄ = 0,508 + 0,167 + 0,312 * 40 = 13,155

d₂₅ = 0,336 + 0,143 + 0,312 * 52 = 16,703

d₂₆ = 0,251 + 0,125 + 0,312 * 64 = 20,344

d₂₇ = 0,2 + 0,111 + 0,312 * 76 = 24,023

d₃₃ = 4,265 + 0,167 + 0,312 * 54 = 21,28

d₃₄ = 1,069 + 0,143 + 0,312 * 81 = 26,484

d₃₅ = 0,508 + 0,125 + 0,312 * 108 = 34,329

d₃₆ = 0,336 + 0,111 + 0,312 * 135 = 42,567

d₃₇ = 0,251 + 0,1 + 0,312 * 162 = 50,895

d₄₄ = 4,265 + 0,125 + 0,312 * 128 = 44,326

d₄₅ = 1,069 + 0,111 + 0,312 * 176 = 56,092

d₄₆ = 0,508 + 0,1 + 0,312 * 224 = 70,496

d₄₇ = 0,336  + 0,09 + 0,312 * 272 = 85,29

d₅₅ = 4,265 + 0,1 + 0,312 * 250 = 82,365

d₅₆ = 1,069 + 0,09 + 0,312 * 325 = 102,559

d₅₇ = 0,508 + 0,083 + 0,312 * 400 = 125,391

d₆₆ = 4,265 + 0,083 + 0,312 * 432 = 139,132

d₆₇ = 1,069 + 0,076 + 0,312 * 540 = 169,625

d₇₇ = 4,265 + 0,071 + 0,312 * 686 = 218,368

Р^н_в = 45,3 + 12,4 = 57,7 кН.

D_0p = 0;

D_1p = - 0,312*((2+5+8+11+14+17+20)*(57,7)) = - 1386,2;

D_2p = - 0,312*((5+16+28+40+52+64+76)*(57,7) = - 5058,6;

D_3p = - 0,312*((8+28+54+81+108+135+162)*(57,7)) = - 10369,3;

D_4p = - 0,312*((11+40+81+128+176+224+272)*(57,7)) = - 16778;

D_5p = - 0,312*((14+52+108+176+250+325+400)*(57,7)) = - 23853,2;

D_6p = - 0,312*((17+64+135+224+325+432+540)*(57,7)) = - 31270,2;

D_7p = - 0,312*((20+76+162+272+400+540+686)*(57,7)) = - 38813,2;

Значение перемещений и свободных членов канонических уравнений