Выбираем трёхступенчатый редуктор Джеймса. Его кинематическая схема изображена на рис.1.
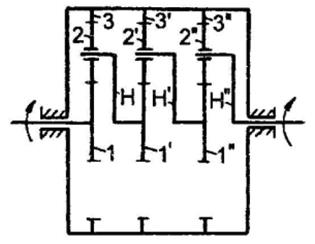
Рис. 1. Кинематическая схема редуктора.
Передаточное отношение всех ступеней принимаем одинаковым и равным
![]() . [3, стр. 138]
. [3, стр. 138]
Определяем количество зубьев:
Числа
зубьев подберем путем совместного решения уравнения передаточного отношения 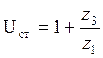 и условия соосности
и условия соосности ![]() , с учетом условия
сборки:
, с учетом условия
сборки:
где:
К – число сателлитов,
Θ – целое число [6, стр. 187].
Исходя
из конструктивных соображений принимаем число зубьев центрального колеса равным
![]() , а число зубьев солнечного колеса
, а число зубьев солнечного колеса ![]()
Проверка по условию сборки:
![]() - целое число, расчет проведен верно.
- целое число, расчет проведен верно.
Исходя из условия соосности, определим число зубьев сателлита:
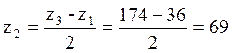 .
.
Определим фактическое передаточное отношение ступени:
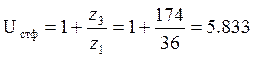
При этом ошибка:
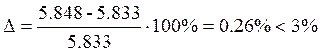
Определим угловые скорости для каждой ступени. Кинематическая схема одной ступени показана на рис. 2:
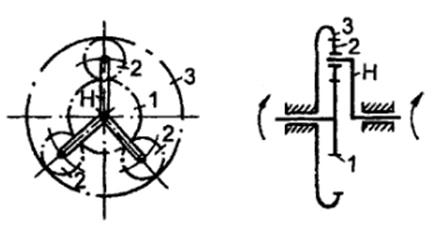
Рис. 2. Кинематическая схема одной ступени редуктора.
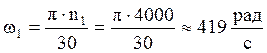 ;
;
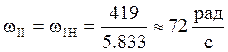 ;
;
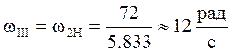
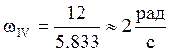
Определим КПД передачи:
![]()
Определим крутящие моменты:
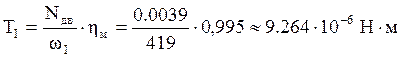 , где ηм – КПД муфты;
, где ηм – КПД муфты;
![]()
где ηз.п. – КПД передачи; ηп – КПД подшипника скольжения;
![]() ;
;
![]() ;
;
![]() .
.
2.2. Расчёт параметров ступеней редуктора
Для расчёта межосевых расстояний ступеней редуктора воспользуемся формулой:
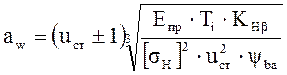 , [4, стр. 135]
, [4, стр. 135]
где Eпр – модуль Юнга (для данного материала Eпр=1,2.103);
Ti
– крутящий момент (Ti=![]() Н.м)
Н.м)
Кнв– коэффициент концентрации нагрузки по контактным напряжениям(=1.13);
– допускаемое контактное напряжение (материал полиамид 610, ГОСТ 10589-87);
![]() – коэффициент ширины зубчатого венца;
– коэффициент ширины зубчатого венца;
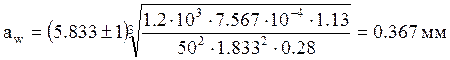 .
.
Модули зубчатых колёс рассчитываем по формуле:
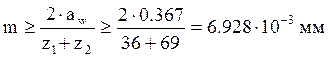 .
.
Примем модули всех зубчатых колес равными m = 0.5 [5, стр. 212], при этом межосевое расстояние станет равным:
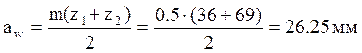 ;
;
тогда ширина зубчатого венца:
![]() .
.
Диаметры делительных окружностей зубчатых колес:
![]() ;
;
![]() ;
;
![]() .
.
Диаметры окружностей вершин:
![]() ;
;
![]() ;
;
![]() .
.
Диаметры окружностей впадин:
![]() ;
;
![]() ;
;
![]() .
.
2.3. Расчёт валов
Предварительный расчёт:
Так как муфта передаёт на вал только крутящий момент, поэтому часть вала с насаженной муфтой работает лишь на кручение. Тогда из условия прочности находим диаметр вала под соединительную муфту:
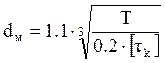 , [5, стр. 371] где
, [5, стр. 371] где ![]() - крутящий момент;
- крутящий момент;
![]() - допускаемое напряжение при кручении,
- допускаемое напряжение при кручении,
![]() ;
;
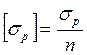 , где n – запас(1.5…5).
, где n – запас(1.5…5).
![]()
Подставляя в формулу конкретные значения, получим:
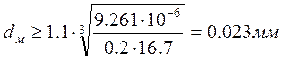 .
.
Так
как диаметр вала двигателя больше, чем диаметр вала под муфту, то примем ![]() .
.
Вследствие незначительных нагрузок диаметры всех остальных валов принимаем равными 4 мм.
2.4. Расчет штифтового соединения
Для
используемого в данной работе муфтового соединения применяются штифты.
Штифтовое соединение, нагруженное крутящим моментом T (=![]() Н.мм), рассчитывается на срез. Запишем условие прочности:
Н.мм), рассчитывается на срез. Запишем условие прочности:
![]() , [5, стр.149]
, [5, стр.149]
где ![]() допускаемое напряжение на сдвиг (для стали
50 МПа),
допускаемое напряжение на сдвиг (для стали
50 МПа),
![]() - сила вызывающая сдвиг (срез) штифта,
где d – диаметр вала;
- сила вызывающая сдвиг (срез) штифта,
где d – диаметр вала;
![]() - площадь поперечного сечения, откуда:
- площадь поперечного сечения, откуда:
![]() .
.
Рассчитаем диаметр штифта:
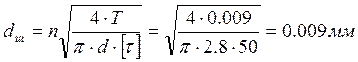
Примем диаметр штифта равным 1 мм, тогда длинна штифта:
![]()
2.5. Расчет и выбор подшипников
Так как осевая нагрузка равна 0, то в качестве всех опор будем использовать радиальные подшипники скольжения. В качестве материала будем использовать углепластик АФ-3Т [1, т. 2 стр. 66], с высоким содержанием порошковых углеродных наполнителей и смол горячего отверждения. Выбор обоснован возможностью таких подшипников работать без смазки, при сложных внешних условиях (запыленность, резкий перепад температур и т. д.). Далее приведена характеристика АФ-3Т (рис. 4)

Рис.4. Характеристика материала для подшипника скольжения
Рассчитаем подшипники под выходной вал. Для этого определим нагрузку на опору. Для последнего зубчатого колеса определи окружную и радиальную силу:
Окружная сила:
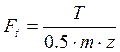 ,
[5, стр. 375], где T – крутящий момент на водиле III ступени передачи(
,
[5, стр. 375], где T – крутящий момент на водиле III ступени передачи(![]() );
);
m – модуль зубчатого зацепления, сателлита и солнечного колеса;
z - чмсло зубьев сателлита.
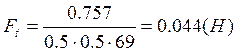 .
.
Радиальная сила:
![]() ,
[5, стр. 375]
,
[5, стр. 375]
![]() .
.
Итак, условие работоспособности по удельному давлению:
![]() , [5, стр. 404]
, [5, стр. 404]
где F – нагрузка на опору, l и d – длинна и диаметр вкладыша,
![]() - допускаемое давление (
- допускаемое давление (![]() =12 МПа). Найдем p:
=12 МПа). Найдем p:
![]()
Запишем критерий теплостойкости:
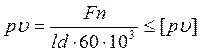 , [5, стр. 404]
, [5, стр. 404]
где n – частота вращения вала (20 об/мин),
![]() - допускаемое значение критерия теплостойкости (
- допускаемое значение критерия теплостойкости (![]() =30 МПа.м/сек)
=30 МПа.м/сек)
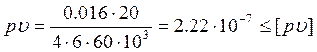
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.