Определение расстояния от точки до прямой линии

Санкт-Петербургский государственный морской технический университет

Кафедра компьютерной графики и информационного обеспечения

ЗАНЯТИЕ 3

ПРАКТИЧЕСКОЕ ЗАДАНИЕ №3

Определение расстояния от точки до прямой линии.

Определить расстояние между точкой и прямой линией можно, выполнив следующие построения (см. рис.1):

·  из точки С опустить перпендикуляр на прямую а;

·  отметить точку К пересечения перпендикуляра с прямой;

·  измерить величину отрезка КС, началом которого является заданная точка, а концом отмеченная точка пересечения.

                         

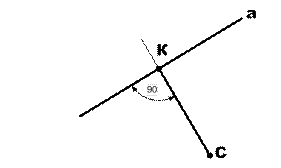
                                      Рис.1. Расстояние от точки до прямой.

В основе решения задач такого типа лежит правило проецирования прямого угла: прямой угол проецируется без искажения, если хотя бы одна его сторона параллельна плоскости проекций (т.е. занимает частное положение). Начнем именно с такого случая и рассмотрим построения  для определения расстояния от точки С до отрезка прямой АВ.

В данном задании нет тестовых примеров, а варианты для выполнения индивидуальных  заданий приведены в таблице1 и  таблице2. Ниже описано решение задачи, а соответствующие построения показаны на рис.2.

1.  Определение расстояния от точки до прямой частного положения.

 Сначала строятся проекции точки и отрезка. Проекция А1В1 параллельна оси Х. Это означает, что отрезок АВ параллелен плоскости П2. Если из точки С провести перпендикуляр к АВ, то прямой угол проецируется без искажения именно на  плоскость П2. Это позволяет провести перпендикуляр из точки С2 на проекцию А2В2.

Падающее меню Чертеж-Отрезок (Draw-Line).  Установить курсор в точку С2 и зафиксировать ее как первую точку отрезка. Сдвинуть курсор по направлению нормали к отрезку А2В2 и зафиксировать на нем вторую точку в момент появления подсказки Нормаль (Perpendicular). Обозначить построенную точку К2. Включить режим ОРТО(ORTHO), и из точки К2 провести вертикальную линию связи до пересечения с проекцией А1 В1_. Точку пересечения обозначить через К1. Точка К, лежащая на отрезке АВ, является точкой пересечения перпендикуляра, проведенного из точки С, с отрезок АВ. Таким образом, отрезок КС является искомым расстоянием от точки до прямой.

Из построений видно, что отрезок КС занимает общее положение и, следовательно, его проекции искажены. Говоря о расстоянии, всегда имеется в виду истинная величина отрезка, выражающего расстояние. Следовательно, надо найти истинную величину отрезка КС, повернув его до частного положения, например, КС|| П1. Результат построений показан на рис.2.

Из приведенных на рис.2 построений, можно сделать вывод: частное положение прямой (отрезок параллелен П1 или П2) позволяет быстро строить проекции расстояния от точки до прямой, но при этом они искажены.

                                     

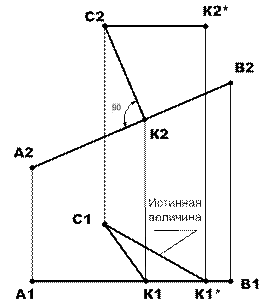
  Рис.2. Определение расстояния от точки до прямой частного положения.

2.  Определение расстояния от точки до прямой общего положения.

Не всегда в начальном условии отрезок занимает частное положение. При общем начальном положении выполняются следующие построения для определения расстояния от точки до прямой:

a)  используя метод преобразования чертежа, перевести отрезок из общего положения в частное – это позволит построить проекции расстояния (искаженные);

b)  вторично используя метод, перевести отрезок, соответствующий искомому расстоянию в частное положение – получим проекцию расстояния по величине, равной действительной.

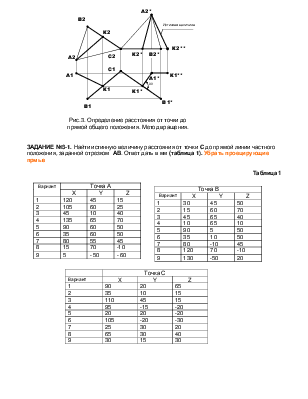
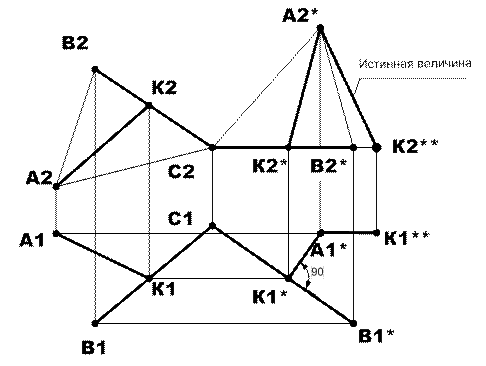
Рассмотрим последовательность построений для определения расстояния от точки А до отрезка общего положения ВС (рис.3).

При первом вращении необходимо получить частное положение отрезка ВC. Для этого в слое ТМР надо соединить точки В2, С2 и А2. Используя команду  Изменить-Повернуть (Modify – Rotate) треугольник В2С2А2  повернуть вокруг точки С2 до положения, когда новая проекция В2*С2 будет располагаться строго горизонтально (точка С неподвижна и, следовательно, ее новая проекция совпадает с первоначальной и обозначения С2* и С1* можно на чертеже не показывать). В результате будут  получены новые проекции отрезка В2*С2 и точки: А2*. Далее из точек А2* и В2* проводятся вертикальные, а из точек  В1 и А1 горизонтальные линии связи. Пересечение соответствующих линий определит положение точек новой горизонтальной проекции: отрезка В1*С1 и точки А1*.

В полученном частном положении можно построить проекции расстояния для этого: из точки А1* строится нормаль к В1*С1. Точка их взаимного пересечения – К1*.Из этой точки проводится вертикальная линия связи до пересечения с проекцией В2*С2. Отмечается точка К2*. В результате получены проекции отрезка АК, являющегося искомым расстоянием от точки А до отрезка прямой ВС.

Далее необходимо построить проекции расстояния в начальном условии. Для этого из точки К1* удобно провести горизонтальную линию до пересечения с проекцией В1С1 и обозначить точку пересечения К1. Затем строится точка К2 на фронтальной проекции отрезка и проводятся проекции  А1К1  и А2К2. В результате построений получены проекции расстояния, но и в начальном и в новом частном положении отрезка ВС, отрезок АК занимает общее положение, а это приводит к тому, что все его проекции искажены.

При втором вращении необходимо повернуть отрезок АК в частное положение, что позволит определить истинную величину расстояния – проекция А2*К2**. Результат всех построений показан на рис.3.

            

ЗАДАНИЕ №3-1. Найти истинную величину расстояния от точки С до прямой линии частного положения, заданной отрезком  АВ. Ответ дать в мм (таблица 1).Убрать проецирующие прмые

Таблица 1

Вариант	Точка А
	Х	Y	Z
1	120	45	15
2	105	60	25
3	45	10	40
4	135	65	70
5	90	60	50
6	35	60	50
7	80	55	45
8	15	70	-10
9	5	- 50	- 60

Точка В
Вариант	X	Y	Z
1	30	45	50
2	15	60	70
3	45	65	40
4	10	65	10
5	90	5	50
6	35	10	50
7	80	-10	45
8	120	70	-10
9	130	-50	20

	Точка С
Вариант	X	Y	Z
1	90	20	65
2	35	10	15
3	110	45	15
4	95	-15	-20
5	20	20	-20
6	105	-20	-30
7	25	30	20
8	65	30	40
9	30	15	30

ЗАДАНИЕ №3-2. Найти истинную величину расстояния от точки M до прямой линии общего положения, заданной отрезком  ED. Ответ дать в мм (таблица 2).

                                                              Таблица 2

Вариант	Точка E
	Х	Y	Z
1	100	45	40
2	110	20	- 40
3	120	60	30
4	130	15	30
5	140	20	- 50
6	150	30	- 45
7	160	50	10
8	170	- 15	70
9	180	60	- 20

Точка D
Вариант	X	Y	Z
1	20	- 60	20
2	25	- 15	- 60
3	15	- 25	60
4	60	20	- 15
5	0	- 65	10
6	10	- 10	85
7	5	5	- 70
8	30	70	- 40
9	20	10	50

Вариант	Точка M
1	70	85	100
2	75	90	105
3	80	100	90
4	60	110	110
5	65	50	80
6	55	70	120
7	70	60	75
8	85	130	100
9	90	110	95

Проверка и зачет  выполненного ЗАДАНИЯ №3.