

Санкт-Петербургский государственный морской технический университет
Кафедра компьютерной графики и информационного обеспечения
ЗАНЯТИЕ 4
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №4
Определение расстояния от точки до плоскости.
1. Определение расстояния от точки до проецирующей плоскости.
Для того, чтобы найти действительную величину расстояния от точки до плоскости, необходимо:
· из точки опустить перпендикуляр на плоскость;
· найти точку пересечения проведенного перпендикуляра с плоскостью;
· определить действительную величину отрезка, началом которого является заданная точка, а концом – найденная точка пересечения.
Плоскость может занимать в пространстве общее и частное положение. Под частным понимается положение, при котором плоскость перпендикулярна к плоскости проекций – такую плоскость называют проецирующей. Основной признак проецирующего положения: плоскость перпендикулярна к плоскости проекций, если она проходит через проецирующую прямую. В этом случае одна из проекций плоскости прямая линия – ее называют следом плоскости.
Если плоскость проецирующая, то легко определить действительную величину расстояния от точки до плоскости. Покажем это на примере определения расстояния от точки В до фронтально-проецирующей плоскости, заданной следом Q2 на плоскости П2 (рис.1).
Плоскость Q перпендикулярна к фронтальной плоскости проекций, следовательно, любая к ней перпендикулярная линия будет параллельна к плоскости П2. А тогда прямой угол на плоскость П2 будет проецироваться без искажения, и можно из точки В2 провести перпендикуляр к следу Q2. Отрезок ВК находится в частном положении, при котором фронтальная проекция В2К2 равна истинной величине искомого расстояния.
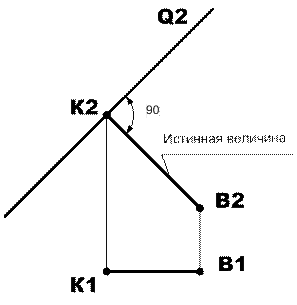
Рис.1. Определение расстояния от точки до проецирующей плоскости.
2. Определение расстояния от точки до плоскости общего положения.
Если плоскость занимает общее положение, то необходимо перевести ее в проецирующее положение. Для этого в ней проводится прямая частного положения (параллельная к одной из плоскостей проекций), которую можно перевести в проецирующее положение, используя одно преобразование чертежа.
Прямая, параллельная плоскости П1, называется горизонталью плоскости и обозначается буквой h. Прямая, параллельная фронтальной плоскости проекций П2, называется фронталью плоскости и обозначается буквой f.Линии hиfназываются главными линиями плоскости. Решение задачи показано на следующем примере (рис.2).
Начальное условие: треугольник АВС задает плоскость. М - точка вне плоскости. Заданная плоскость занимает общее положение. Для перевода ее в проецирующее положение выполним следующие действия. Включить режим ОРТО (ORTHO), использовать команду Отрезок (Line) – провести любую горизонтальную линию, пересекающую фронтальную проекцию треугольника А2В2С2 в двух точках. Проекция горизонтали, проходящей через эти точки, обозначена h2. Далее строится горизонтальная проекция h1.
Главная линия hможет быть преобразована в проецирующее положение, при котором заданная плоскость также станет проецирующей. Для этого необходимо повернуть горизонтальные проекции всех точек (вспомогательный четырехугольник АВСМ) в новое положение, при котором линия h1 будет занимать вертикальное положение, перпендикулярное к оси Х. Удобно выполнить эти построения, используя плоскопараллельный перенос (копия проекции помещается на свободное место экрана).
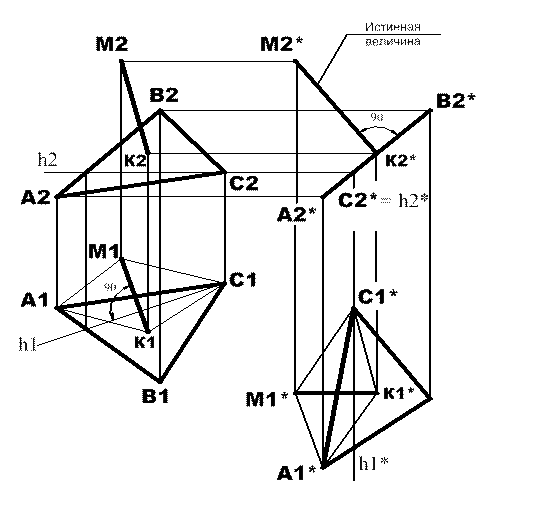
В результате новая фронтальная проекция плоскости будет выглядеть в виде прямой линии (следа плоскости) А2*В2*. Теперь из точки М2* можно провести перпендикуляр к следу плоскости. Новая фронтальная проекция М2*К2* = МК т.е. является искомым расстоянием от точки М до заданной плоскости АВС.
Далее необходимо построить проекции расстояния в начальном условии. Для этого из точки М1 проводится отрезок, перпендикулярный к линии h1, и на нем следует отложить от точки М1 отрезок, равный по величине М1*К1*. Чтобы построить фронтальную проекцию точки К2 из точки К1 проводится вертикальная линия связи, а из точки К2* горизонтальная. Результат построений показан на рис.2.

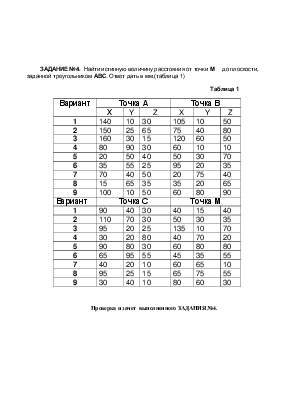
ЗАДАНИЕ №4. Найти истинную величину расстояния от точки М до плоскости, заданной треугольником АВС. Ответ дать в мм.(таблица 1)
Таблица 1
|
Вариант |
Точка А |
Точка В |
||||
|
Х |
Y |
Z |
X |
Y |
Z |
|
|
1 |
140 |
10 |
30 |
105 |
10 |
50 |
|
2 |
150 |
25 |
65 |
75 |
40 |
80 |
|
3 |
160 |
30 |
15 |
120 |
60 |
50 |
|
4 |
80 |
90 |
30 |
60 |
10 |
10 |
|
5 |
20 |
50 |
40 |
50 |
30 |
70 |
|
6 |
35 |
55 |
25 |
95 |
20 |
35 |
|
7 |
70 |
40 |
50 |
20 |
75 |
40 |
|
8 |
15 |
65 |
35 |
35 |
20 |
65 |
|
9 |
100 |
10 |
50 |
60 |
80 |
90 |
|
Вариант |
Точка С |
Точка М |
||||
|
1 |
90 |
40 |
30 |
40 |
15 |
40 |
|
2 |
110 |
70 |
30 |
50 |
30 |
35 |
|
3 |
95 |
20 |
25 |
135 |
10 |
70 |
|
4 |
30 |
20 |
80 |
40 |
70 |
20 |
|
5 |
90 |
80 |
30 |
60 |
80 |
80 |
|
6 |
65 |
95 |
55 |
45 |
35 |
55 |
|
7 |
40 |
20 |
10 |
60 |
65 |
10 |
|
8 |
95 |
25 |
15 |
65 |
75 |
55 |
|
9 |
30 |
40 |
10 |
80 |
60 |
30 |
Проверка и зачет выполненного ЗАДАНИЯ №4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.