Определение абсолютной, относительной и приведенной погрешности результата измерения. Построение графиков погрешностей на диапазоне измерений, страница 2

Так как округлять результат следует так, чтобы он оканчивался цифрой того же разряда, что и значение погрешности, то в нашем случае будем иметь:

(-67,34 ± 0,12) кОм

7) Строим графики абсолютной, относительной и приведенной погрешностей на диапазоне измерений:

Задача  №3

Вариант	Исходные данные
	Класс точности c/d	Диапазон измерений, мВ	Показание, мВ
5	1,0/0,1	-10…+10	+4,34

Требуется:

1.  Определить абсолютную, относительную и приведенную погрешности результата измерения;

2. Записать результат измерения с указанием его погрешности;

3. Построить графики абсолютной, относительной и приведенной погрешностей на диапазоне измерений.

1) Составим таблицу:

V, В	∆V, В	δV, %	γV, %
-10	±0,07	±0.7	±0.35
-5	±0,035	±0.5	±0.175
0	±0,02	±∞	±0.1
5	±0,035	±1.3	±0.175
10	±0,07	±1,1	±0.35

2)  Класс точности задан отношением 1,0/0,1, следовательно, относительная погрешность δ_V, % во всех точках шкалы должна удовлетворять следующему отношению:

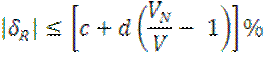
c = 1,0; d = 0,1

За нормируемое значение V_N принимаем размах шкалы, т.к. она содержит 0 ⟹ V_N = 20

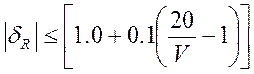
Решаем для самого худшего варианта. Приравняем неравенство:

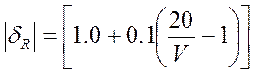
При V = - 10 мВ;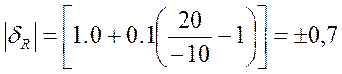

При V = - 5 мВ;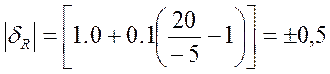

При V = 0 мВ;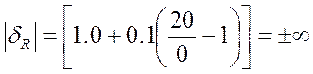

При V = 5 мВ;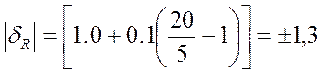

При V = 10 мВ;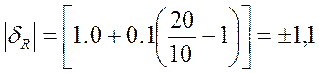

3) Найдем абсолютную погрешность ∆_V:

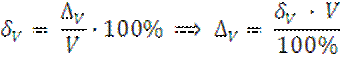
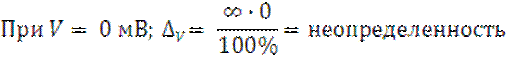
Исключительное значение ∆_V определяется следующим образом, так как класс точности задан двумя числами, то у данного прибора аддитивная и мультипликативная погрешность соизмеримы. При V = 0 мультипликативная составляющая равна 0, значит общая погрешность в этой точке обусловлена только аддитивной составляющей, её представляет второе число, d = 0.1. Это значит, что аддитивная погрешность составляет 0.1 % от верхнего предела измерения прибора, т.е. V_N = 20  

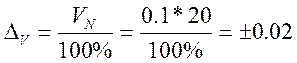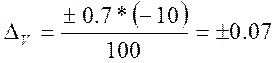При V = 0 мВ;  мВ;

При V 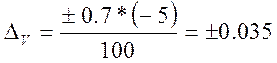= -10;   мВ;

При V = -5;   мВ;

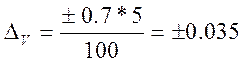При V = 5;   мВ;

При V = 10; 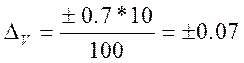  мВ;

4) Рассчитаем приведенную погрешность γ_v, %:

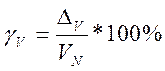
При V = 0 мВ;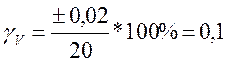

При V = -10;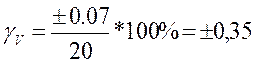

При V = -5;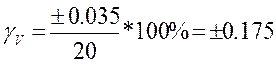

При V = 5;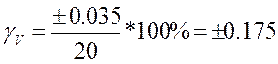

При V = 10;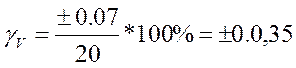

5) Запишем результат измерения с указанием его погрешности:

V = 4.34 мВ;

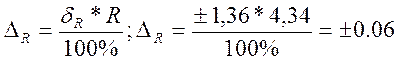
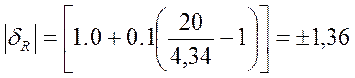
Так как округлять результат следует так, чтобы он оканчивался цифрой того же разряда, что и значение погрешности, то в нашем случае будем иметь:

(1.36 ± 0,06) мВ

6) Строим графики абсолютной, относительной и приведенной погрешностей на диапазоне измерений:

Задача  №4

Вариант	Исходные данные
	Класс точности	Длина шкалы, мм	Показание, Ом	Отсчет
5	4,0	50	2	34

Требуется:

1.  Определить абсолютную, относительную и приведенную погрешности результата измерения;

2. Записать результат измерения с указанием его погрешности;

1) Составим таблицу:

R, Ом	∆R, Ом	δR, %	γR, %
34	±0.64	±1,88	±4
35	±0.64	±1,83	±4
40	±0.64	±1.6	±4
45	±0.64	±1.43	±4
50	±0.64	±1.28	±4

2)  Класс точности задан числом со знаком радикала, следовательно, приведенная погрешность γ_R, % во всех точках шкалы не должна превышать по модулю класса точности:

3) Рассмотрим худший случай, когда приведенная погрешность принимает максимальное по абсолютной величине значение:

 и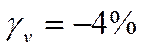

4) Найдем абсолютную погрешность ∆_R:

 

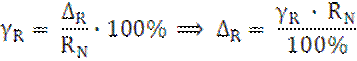
За нормируемое значение R_N принимаем размах шкалы, он будет равен:

 

Значит  _, будет равно:

 

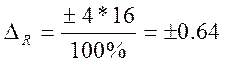
5) Рассчитаем значение относительной погрешности δ_R, %:

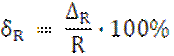
При R = 34 Ом;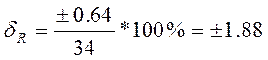

При R = 35 Ом;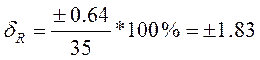

При R = 40 Ом;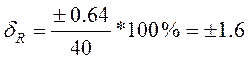

При R = 45 Ом;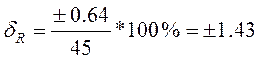

При R = 50 Ом;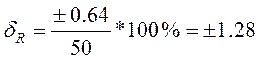

6) Строим графики абсолютной, относительной и приведенной погрешностей на диапазоне измерений

7) Записать результат измерения с указанием его погрешности:

Результат измерения равен 2 Ом и абсолютная погрешность ∆_R остается всегда постоянной, следовательно, результат измерения с указанием погрешности будет выглядеть так:

(2 ± 1,11) Ом