Погрешность может быть абсолютной, относительной и приведенной.
Абсолютная погрешность измерения Δ представляет собой разность между измеренной величиной и действительным значением этой величины:
![]() . (1.2)
. (1.2)
Абсолютная погрешность выражается в единицах измеряемой величины. Однако она не может в полной мере служить показателем точности измерений, т.к. не характеризует качество измерения. Например, погрешность в 1 мм (Δ = 1 мм) при измерении метровых расстояний означала бы необычайно точное измерение, в то время как та же погрешность в 1 мм для расстояния 10 мм не более как грубая приближенная оценка. Для характеристики качества измерения служит относительная погрешность.
Относительная погрешность измерения δ представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
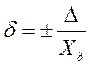 .
(1.3)
.
(1.3)
Поскольку относительная погрешность хорошего измерения обычно малое число, ее умножают на 100 и выражают в процентах:
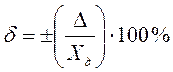 .
(1.4)
.
(1.4)
Для выше указанного примера в первом
случае S = (1±0,001) м 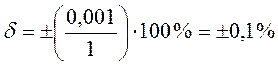 ; во
втором – для S = (10±1) мм
; во
втором – для S = (10±1) мм 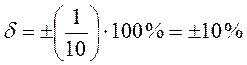 .
.
Относительная погрешность обычно существенно изменяется вдоль шкалы аналогового прибора: с уменьшением значений измеряемой величины она увеличивается вплоть до бесконечности при Х = 0. Поэтому не рекомендуется производить измерения в первой половине шкалы аналоговых приборов, т.к. погрешность здесь может быть значительной. В связи с этим для нормирования погрешности средств измерений используется еще одна разновидность погрешности – приведенная.
Приведенная погрешность измерения γ представляет собой отношение абсолютной погрешности к условно принятому значению величины, постоянному на всем диапазоне измерений:
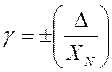 .
(1.5)
.
(1.5)
Во многих случаях приведенную погрешность выражают в процентах:
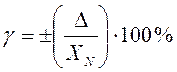 .
(1.6)
.
(1.6)
Условно принятое значение величины называют нормирующим значением ХN.
Приведенная погрешность не остается постоянной для различных отметок шкалы, как по величине, так и по знаку, но не может превышать некоторого значения, установленного для данного прибора в соответствии с его классом точности.
2 КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ПО ЗАВИСИМОСТИ
АБСОЛЮТНОЙ ПОГРЕШНОСТИ ОТ ЗНАЧЕНИЙ
ИЗМЕРЯЕМОЙ ВЕЛИЧИНЫ
Аддитивная погрешность а (Δа) (рисунок 1) не зависит от чувствительности прибора и является постоянной для всех значений входной величины в пределах диапазона измерений. Примеры и причины возникновения аддитивных погрешностей: трение в опорах электроизмерительных приборов; помехи, шумы, погрешность дискретности (квантования) в цифровых приборах; постоянный груз на чашке весов; неточная установка на нуль стрелки прибора перед измерением; термо-ЭДС в цепях постоянного тока. Если прибору присуща только аддитивная погрешность или существенно превышает другие составляющие, то целесообразно нормировать только абсолютную погрешность.
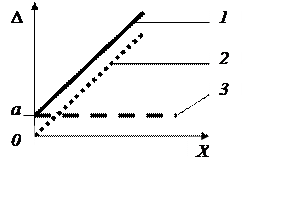 |
Рисунок 1 – Суммарная (1), мультипликативная (2)
и аддитивная погрешности (3)
Мультипликативная погрешность bx (Δм) (рисунок 1) зависит от чувствительности прибора и изменяется прямо пропорционально текущему значению входной величины. Примеры и причины возникновения мультипликативных погрешностей: погрешности изготовления добавочного резистора в вольтметре или шунта в амперметре; погрешность
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.