Исследование временных и частотных характеристик детерминированных сигналов (лабораторная работа)

Спектр напряжения для

U(t)=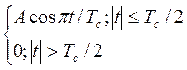

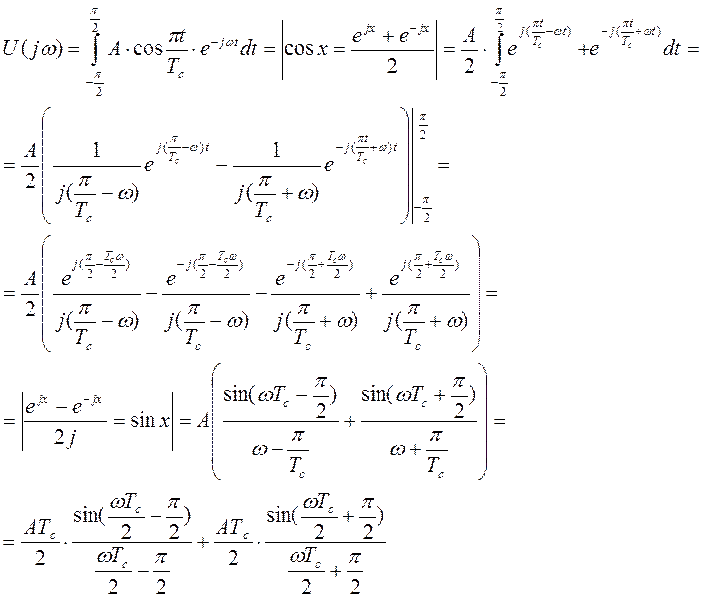
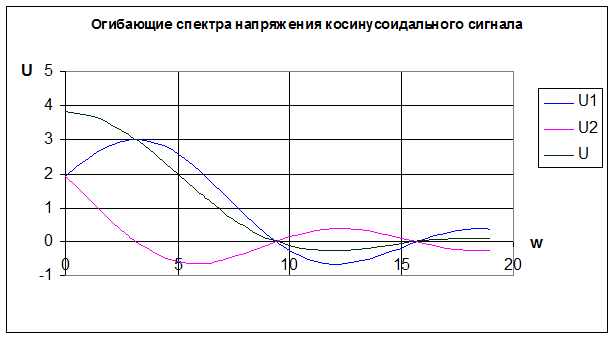
T_c=1     A=6

1.Построение формы сигнала, заданного аналитическим выражением:

а). Прямоугольный сигнал длительности Т_с=5с и амплитуды А=5В

б). Приподнятый косинусоидальный сигнал длительности Т_с=5с и амплитуды А=5В

2. Исследование спектра напряжения сигналов

N – число гармоник

n	Прямоугольный сигнал			Приподнятый косинусоидальный
	N=9	N=15	N=24	N=9	N=15	N=24
1	25	25	25	25	25	25
2	22,5	22,5	22,5	24	24	24
3	16	16	16	21,2	21,2	21,2
4	7,5	7,5	7,5	17,1	17,1	17,1
5	0	0	0	12,5	12,5	12,5
6	-4,5	-4,5	-4,5	8	8	8
7	-5,3	-5,3	-5,3	4,2	4,2	4,2
8	-3,2	-3,2	-3,2	1,6	1,6	1,6
9	0	0	0	0	0	0
10	0	2,5	2,5	0	-0,6	-0,6
11	0	3,1	3,1	0	-0,6	-0,6
12	0	2	2	0	-0,3	-0,3
13	0	0	0	0	0	0
14	0	-1,7	-1,7	0	0,2	0,2
15	0	-2,2	-2,2	0	0,2	0,2
16	0	0	-1,4	0	0	0,1
17	0	0	0	0	0	0
18	0	0	1,3	0	0	-0,1
19	0	0	1,7	0	0	-0,1
20	0	0	1,1	0	0	-0,05
21	0	0	0	0	0	0
22	0	0	-1	0	0	0,04
23	0	0	-1,3	0	0	0,05
24	0	0	-0,9	0	0	0,03
25	0	0	0	0	0	0

Все полученные значения представлены на графиках:

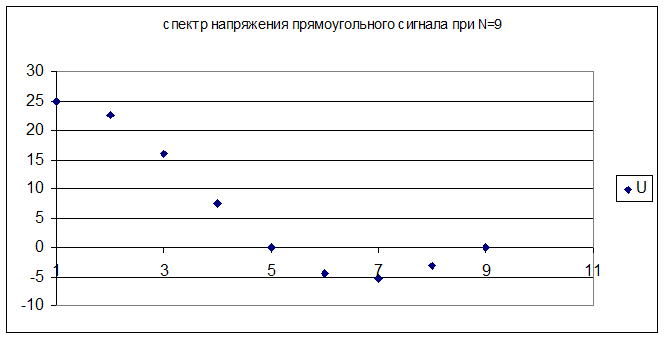
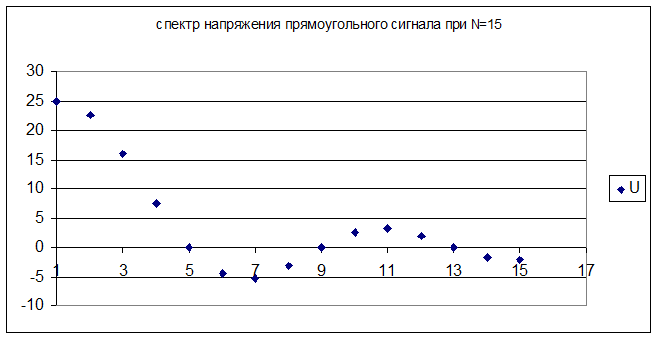
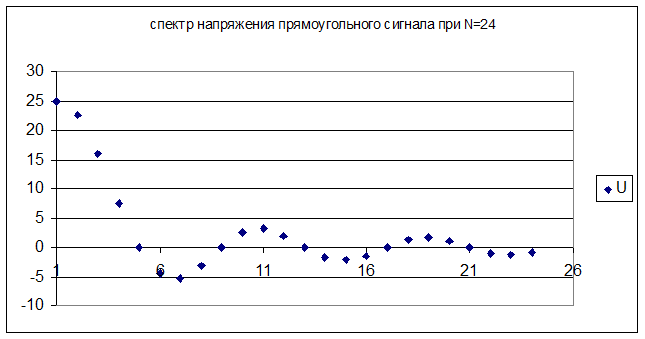
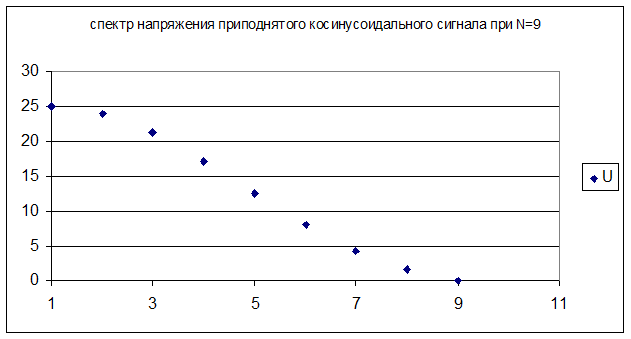
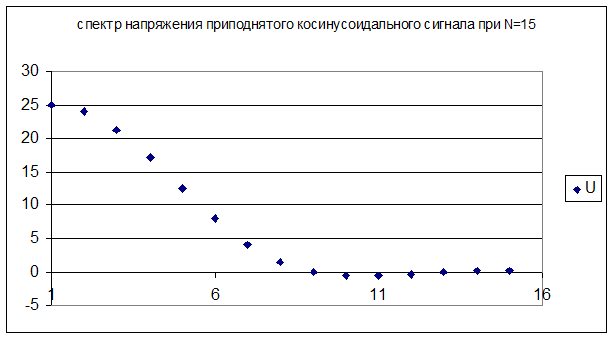
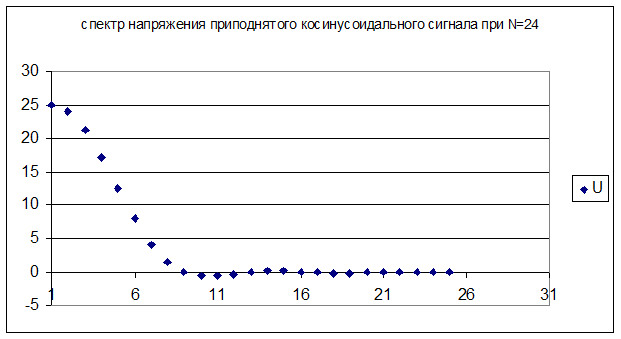
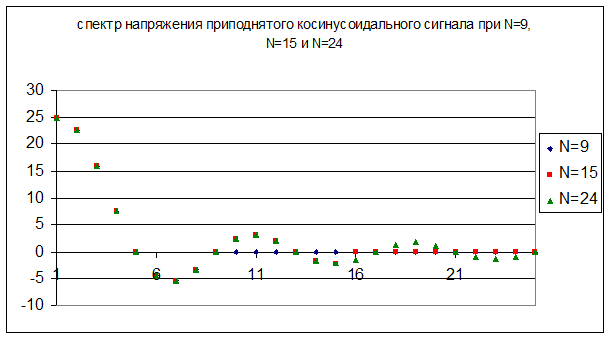
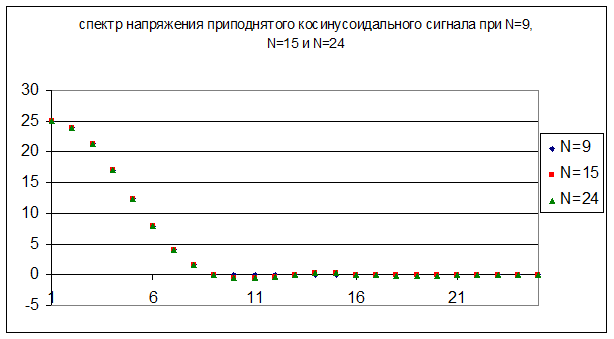
Вывод: ограничение спектра меньше влияет на амплитуду косинусоидального сигнала.

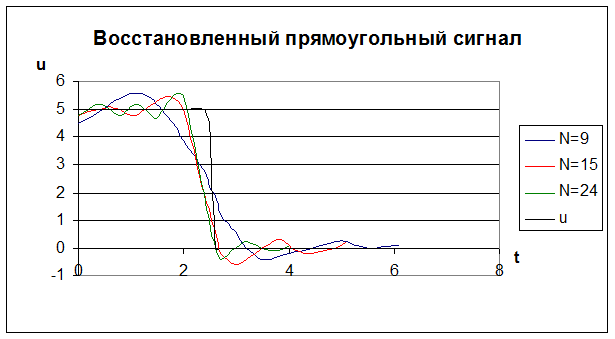
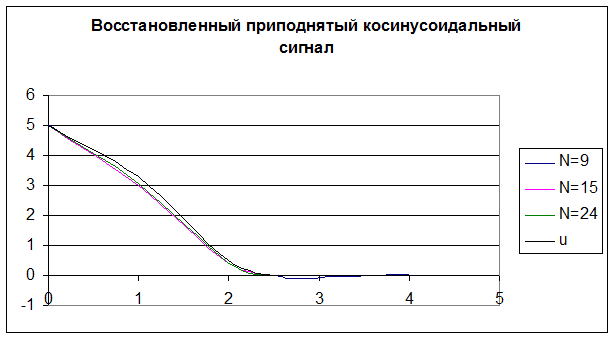
3. Восстановление формы сигнала при ограничении спектра:

Прямоугольный сигнал
t	N=9	N=15	N=24
0	4,5	4,8	4,8
0,2	4,7	4,9	5
0,4	4,9	5	5,2
0,6	5,2	5,1	5
0,8	5,4	5	4,8
1	5,6	4,8	5,1
1,1	5,6	4,8	5,2
1,2	5,6	4,9	5,1
1,4	5,4	5,2	4,8
1,5	5,2	5,3	4,7
1,6	5	5,4	4,9
1,8	4,5	5,4	5,5
2	3,9	5	5,5
2,4	2,8	2	2
2,5	2,2	1,4	1
2,6	1,9	0,6	0
2,7	1,2	-0,2	-0,4
3	0,6	-0,6	0
3,2	0	-0,4	0,2
3,5	-0,4	0	0
3,8	-0,3	0,3	-0,1
4	-0,2	0,1	0,1
4,3	-0,1	-0,2
4,9	0,2	0
5,1	0,2	0,2
5,5	0
6,1	0,1

Приподнятый косинусоидальный сигнал
t	N=9	N=15	N=24
0	5,05	5	5
1	3	3	3,1
2	0,4	0,4	0,4
2,5	0	0	0
2,7	-0,1	0	0
4	0,04	0	0

Вывод: с увеличением числа гармоник происходит лучшее восстановление формы сигнала. При этом наблюдается увеличение частоты пульсаций с уменьшением их амплитуды. Следует отметить резкий выброс на заднем фронте прямоугольного сигнала, который увеличивается с увеличением числа гармоник. В сигнале косинусоидальной формы, т. к. там нет резкого ограничения сигнала, подобный эффект отсутствует, что позволяет точнее передать форму сигнала.

Петербургский

Государственный Университет

Путей Сообщения

Кафедра «Электрическая связь»

Лабораторная работа №1

Исследование  временных

и  частотных  характеристик

детерминированных  сигналов

                         Выполнили студенты гр. АТ-403

Никитин А.В.

Малкевич В.Ю.

Климов М. В.

                                              Проверила: Тулугорова Е. А.

Санкт-Петербург

2006