данной работе рассматривается циклический систематический (n,k) – код, где n – общее число символов кодовой комбинации, k – число информационных символов в кодовой комбинации. Систематическим называется такой код, в котором может быть указано место положения информационных символов, при этом информационными являются первые k символов, а n – k последующих – проверочными. Код называется циклическим, если путём сдвига на один разряд вправо (влево) исходной комбинации, принадлежащей этому коду, получается кодовая комбинация также принадлежащая этому коду. Цикл завершается при n – кратном сдвигу исходной кодовой комбинации. Сдвиг на 1 разряд исходной комбинации равносилен умножению формальной переменной x на соответствующий полином. Приведём пример:
Пусть V(x) = a0x0+a1x1+...+an-1xn-1, тогда xV(X) =
x(a0x0+a1x1+...+an-1xn-1) =
= a0x+a1x2+...+an-2xn-1+an-1xn.
Во избежание удлинения, а, следовательно, превышения максимальной степени многочлена n – 1 следует xn заменить на единицу:
xV(x) = an-1x0+a0x1+a1x2+...+an-2xn-1.
Таким образом, получается кодовая комбинация, принадлежащая тому же коду, что и V(x).
Согласно исходным данным, для канала характерны тройные смежные шибки. Тогда параметры (n,k) – кода определяются по формулам:
2к = 2*А*В
Где: А – количество станций, В – стрелок на каждой станции,2 – состояние стрелки
2k-n > 3n - 2
Таким образом:
2k = 2*35*20
k = 10 Методом подбора: n = 16
Таким образом, получаем, что код имеет параметры (16,10).
Структурная схема передачи дискретной информации:
2.2. Структура цикла опроса.
Согласно заданию, опрос ведется между конечными станциями. Схематично тракт передачи сигналов выглядит следующим образом
 |
А - станция, передающая информацию
В - конечная станция, принимающая информацию
Учитывая, что количество импульсов синхросигнала равно 3, а общее число элементов n кодовой комбинации 16, построим структуру цикла опроса станций и стрелок в канале ТУ:
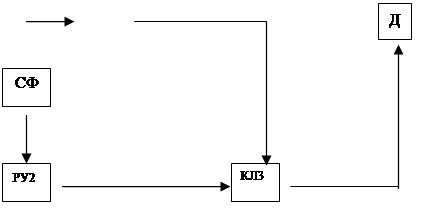
2.3 Структурная схема приемного устройства, устанавливаемого на конечной станции.
Используем следующие устройства:

- генератор тактовых импульсов;

согласованный фильтр СИНХРОСИГНАЛА

- решающее устройство;
- согласованный фильтр;
 |
- ключ;

- линия задержки;

- декодер.
 |
|||||
|
|
||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() КЛ2
КЛ2
![]()
![]()
![]()
![]()
|
 |
|||
2.4. Производящий многочлен g(x).
Циклическим (n,k) – кодом также называют код, все кодовые полиномы которого являются кратными некоторому полиному - порождающему (производящему) – g(x). Производящий многочлен g(x) находится методом подбора и должен удовлетворять трём условиям:
1. Старшая степень g(x) = n – k
2. Многочлен xn+1 должен делиться на g(x) без остатка.
3. Многочлен g(x) должен быть разложим.
Выберем g(x) вида:
g(x) = x6 +x4+x2+1
Проверим три условия, которым должен удовлетворять производящий многочлен g(x), если известно, что n = 16, k = 10.
1. n – k = 16 – 10 = 6
Таким образом, первое условие выполняется. То есть старшая степень g(x) равна 6, что и наблюдается в выбранном многочлене g(x).
![]() 2.
2.
![]() x16+1 x6 +x4 +x2+1
x16+1 x6 +x4 +x2+1
x16+x14+x12+x10 x10+x8+x2+1
x14+x12+x10 +1
x14+x12+x10+x8
x8+1
x8+x6+x4+x2
x6+x4+x2+1
x6+x4+x2+1
0
Как видно остаток от деления x16+1 на g(x) равен 0. Следовательно, и второе условие выполняется.
Очевидно, что x6 +x4 +x2+1 (x6+x4+x2+1=x4(x2+1)+(x2+1)=(x2+1) (x4+1)) разложим, то есть и третье условие выполняется.
2.5. Определение кодовой комбинации теоретически.
Кодирование циклических систематических кодов осуществляется по приведённому ниже алгоритму. Кодирование произведём для кода (16,10), производящий член которого g(x) = x6 +x4+x2+1:
1. Выбирается информационная комбинация, старшая степень которой равна
К-1, и представляется в виде многочлена l(x).
l(x) = x8 +x6 +x5 +x4 +1
l(x)=1000111010
2. Информационный многочлен l(x) умножаем на xn-k.
I(x)xn-k = (x8 +x6 +x5 +x4 +1)x6 = x14+x12+x11+x10+ x6
3. Полученный многочлен делится на производящий g(x).
![]() x14+x12+x11+x10+ x6x6+x4+x2+1
x14+x12+x11+x10+ x6x6+x4+x2+1
X14+x12+x10+x8 x8+x5+x3+x2
X11+x8+x6
X11+x9+x7+x5
X9+x8+x7+x6+x5
X9+x7+x5+x3
X8+ x6+x3
X8+x6+x4+x2
x4 +x3 +x2 R(x)= x4 +x3 +x2
4. Остаток от деления R(x) суммируется с l(x)xn-k в результате чего получаем кодовую комбинацию V(x): V(x) = l(x)xn-k + R(x).
Таким образом, получаем:
V(x) = x14+x12+x11+x10+ x6 + x4 +x3 +x2 V(x)=001110100011101
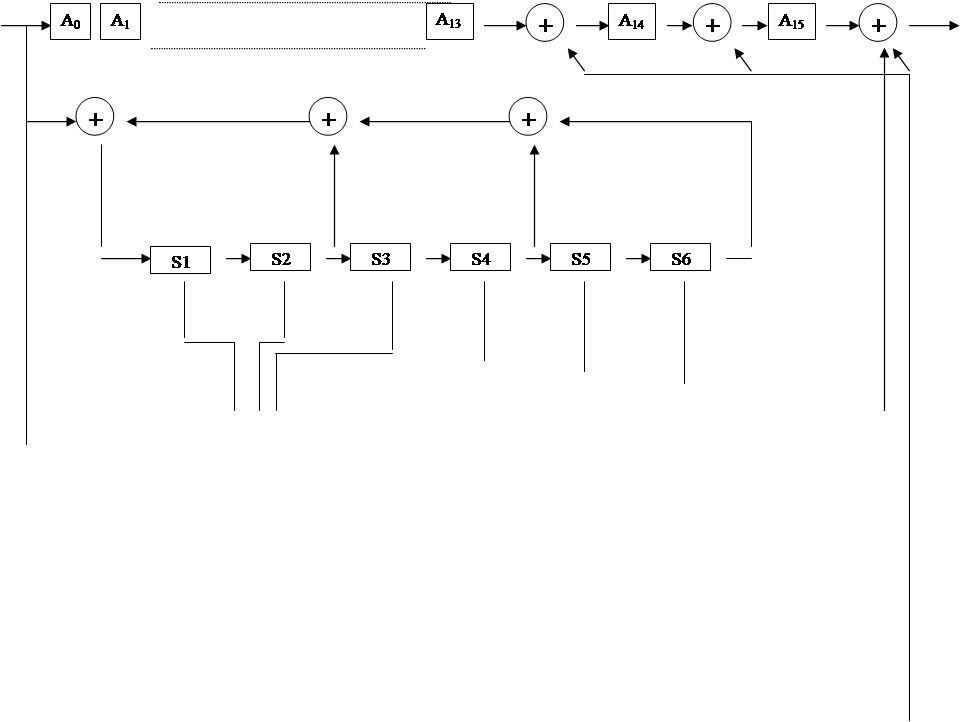
2.6. Структурная схема кодера.
Схема кодера состоит из:
¨ элементов регистра сдвига (D – триггеров), число которых равно старшей степени производящего многочлена g(x);
¨ сумматоров по модулю 2, число которых равно числу знаков сложения в производящем многочлене g(x).
Выше был подобран производящий многочлен для кода (16,10) вида:
g(x) = x6+x4+x2+1
Тогда в схема кодера будет содержать 6 элементов регистра сдвига и 3 сумматора. Примем следующие обозначения:
|
- элемент регистра сдвига (D – триггер)

- сумматор
к - ключ
Схема кодера будет иметь вид:
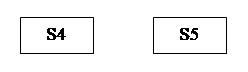 |
||||||||||||
|
|
|
|
|||||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
g6 g4 g2 g0
 |
|||
 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
2![]()
![]()
к
1 l(x)
V(x) ![]()
![]()
2.7. Таблица состояний элементов регистра сдвига кодера систематического кода.
Для описания работы схемы кодера составляются уравнения функционирования элементов регистра сдвига. При этом вводится понятие задержки на один такт; Запаздывание на один такт обозначим символом D. Тогда функционирование схемы будут определять следующие уравнения:
1.Ключ в положении 1 2.Ключ в положении 2
S1 = D( l+S2+S4+S6) S1 = 0
S2 = DS1 S2 = DS1
S3 = DS2 S3 = DS2
S4 = DS3 S4 = DS3
S5 = DS4 S5 = DS4
S6 = DS5 S6 = DS5
V(x) = l(x) V(x) = S2+S4+S6
Работу схемы отобразим в виде таблицы функционирования. Первым поступает импульс, соответствующий большей степени l(x):
|
Такт |
Положение ключа |
l(x) |
Состояние элементов |
V(x) |
|||||
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
||||
|
1 |
1 2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
4 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
5 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
6 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|
7 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
8 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
9 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
10 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
|
12 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
13 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
14 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
На выходе кодера получили кодовую комбинацию V = 001110100011101. Теперь представим её в виде полинома и убедимся, что мы получили туже кодовую комбинацию, что и теоретически:
V(x) = x14+x12+x11+x10+ x6 + x4 +x3 +x2
2.8. Теоретический синдром одиночной, двойной и тройной смежной ошибки.
2.9. Структурная схема генератора синдромов. Аппаратный синдром ошибки.
Схема генератора синдромов представляет собой схему деления. Она состоит из тех же элементов, что и кодер, причём количество элементов определяется по тем же правилам. Построим схему генератора синдромов.
Для одиночной ошибки:
 |
||||||||||||
|
|
|
|
|||||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
g6 g4 g2 g0
 |
|||
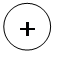 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
V(x)
Уравнения состояний:
S1 = D( V(x) +S2+S4+S6)
S2 = DS1
S3 = DS2
S4 = DS3
S5 = DS4
S6 = DS5
Таблица состояний:
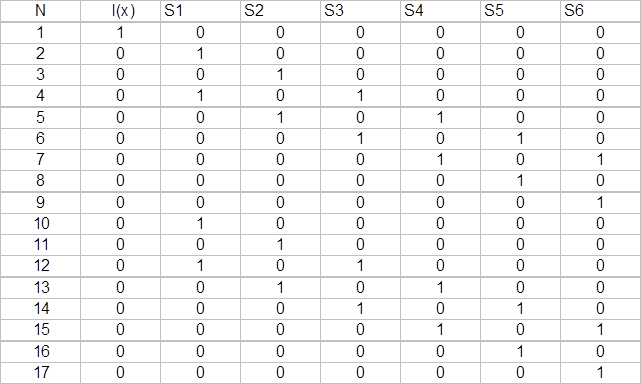
Для тройной ошибки:
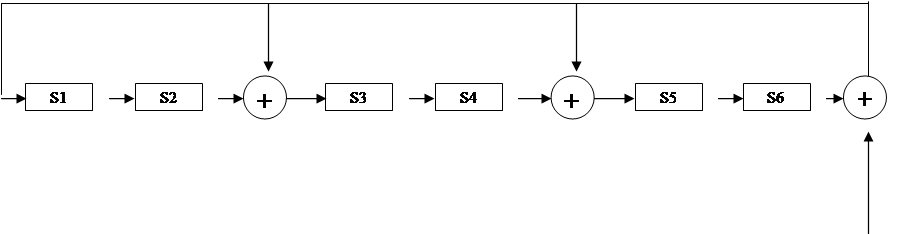
Уравнения состояний:
S1 = D(V(x)+S6) V(x)
S2 = DS1
S3 = D(V(x)+S2+S6)
S4 = DS3
S5 = D(V(x)+S4+S6)
S6 = DS5
Таблица состояний:
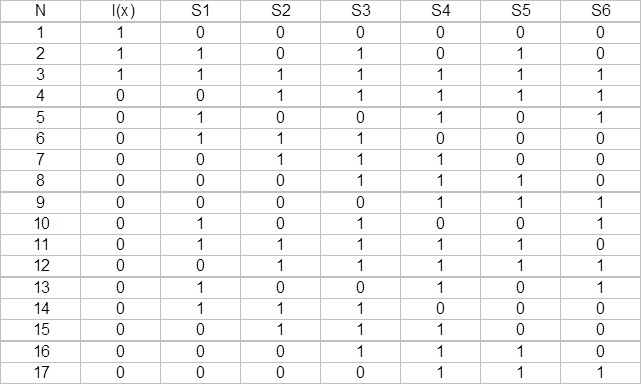
2.10.Таблица состояний элементов регистра сдвига генератора синдромов на примере ошибочно принятой кодовой комбинации.
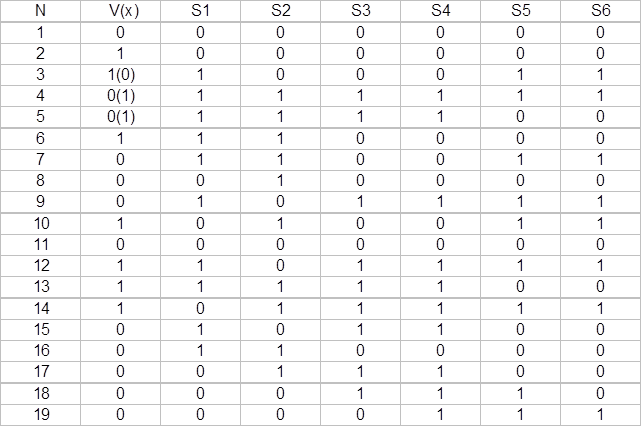
2.11. Структурная схема декодера.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|

![]()
![]()
![]()
![]()
![]()
![]()
 |
|||
2.12. Расчёт амплитуды импульсов на входе канала ТУ и длительности импульсов.
Рассчитаем длительность импульсов Ти по формуле:
Ти = Тпер/N
Тпер – время опроса (мин);
N – Общее количество элементов в структуре цикла.
N = N кол.синхр. + N кол.ст.* n
Подставляя значения из исходных данных, получаем:
N = 3 + 35 * 16 = 563
Ти = 2.1/563 = 0,003 мин
Для нахождения Амплитуды импульсов на входе канала ТУ используем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.