Исследование дискретного источника информации (длина сообщения n=100, число букв в алфавите N=3, перечень букв A=(1,2,3))

Петербургский Государственный Университет Путей Сообщения

Кафедра «Электрическая связь»

Отчет по лабораторной работе №5

«Исследование дискретного источника информации»

Выполнил студент     группы АТК-102

Лебединский А.А.

Проверил

Сидорович Д.Ю.

Санкт-Петербург

2003

Исходные данные:

Вариант 5.

12333211123332323233

32221122221133321133

32332323332233321133

32112333221122333223

21123332111132321132

Цель работы:

Закрепление теоретических знаний о моделях дискретных источников информации и их свойствах. Приобретение навыков статистических исследований сообщений источников и определения их информационных характеристик, а также навыков статистического кодирования.

Содержание работы:

1.  Определение статистических характеристик источника по заданному сообщению.

2.  Определение информационных характеристик источника и оценка влияния на них неравновероятности и взаимозависимости букв.

3.  Статистическое кодирование сообщений источника без учета и с учетом взаимозависимости букв, оценка эффективности различных способов статистического кодирования.

Выполнение работы:

1.  Определение статистических характеристик источника по заданному сообщению.

1.1  Длина сообщения n=100, число букв в алфавите N=3, перечень букв A=(1,2,3).

1.2  Вероятности появления букв в сообщении:

1.3  Вероятности двухбуквенных сочетаний:

1.4  Тип источника – марковский, т.к. буквы взаимозависимы.

1.5  Переходные (условные) вероятности:

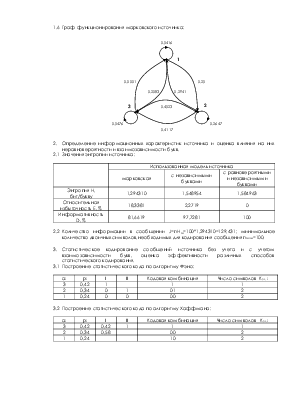
1.6  Граф функционирования марковского источника:

2.  Определение информационных характеристик источника и оценка влияния на них неравновероятности и взаимозависимости букв.

2.1  Значения энтропии источника:

2.2  Количество информации в сообщении J=nH_м=100*1,294310=129,431; минимальное количество двоичных символов, необходимых для кодирования сообщения n_мин=100.

3.  Статистическое кодирование сообщений источника без учета и с учетом взаимозависимости букв, оценка эффективности различных способов статистического кодирования.

3.1  Построение статистического кода по алгоритму Фэно:

3.2  Построение статистического кода по алгоритму Хаффмана:

3.3  Количество букв статистического кода, необходимое для кодирования стобуквенного источника n_СТ.И=158 букв.

3.4  Эффективность статистического кодирования:

Вывод:

В процессе работы были закреплены теоретические знания о моделях дискретных источников информации и их свойствах. Приобретены навыки статистических исследований сообщений источников и определения их информационных характеристик, а также навыки статистического кодирования. При построении статистических кодов для кодирования сообщений по отдельным буквам и по двухбуквенным сочетаниям, можно заключить, что кодирование двухбуквенным сочетанием эффективнее.