Изучение свойств дискретного канала и его параметров

Санкт-Петербургский Государственный Университет Путей Сообщения.

Кафедра: «Электрическая связь»

Лабораторная работа № 5

«Исследование канала передачи информации»

Вариант №8

Выполнили студенты гр. АТ-503                                                                    Калачёв В.О.

Пилипенко Е.О.

Проверил преподаватель                                                                          Котов В.К.

Санкт-Петербург

2007г.

1. Исходная матрица вероятностей появления букв.

                

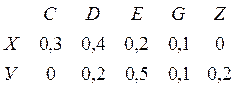
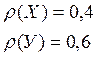
Характеристика канала:

А. Недвоичный

Б. Несимметричный по выходу

В. Источник – с неравной вероятностью и взаимонезависимостью букв

2. Граф матрицы:

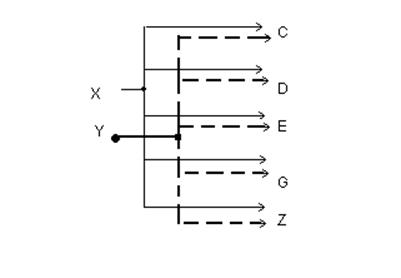
3. Формулы нахождения вероятностей.

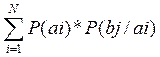
            X, Y – исходные буквы на входе системы

                                                                           - буква, полученная на выходе системы

P(C) = 0,4*0,3+0,6*0 = 0,12

P(D)= 0,4*0,4+0,6*0,2 = 0,28

P(E) = 0,4*0,2+0,6*0,5 = 0,38

P(G) = 0,4*0,1+0,6*0,1 = 0,1

P(Z) = 0*0+0,6*0,2 = 0,12

4.Формулы нахождения обратных условных вероятностей.

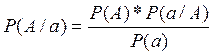
P(X/C) = 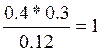                                   P(Y/C) = 0

P(X/D) = 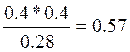                               P(У/D) = 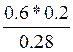=0.42

P(X/E) = 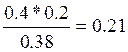                               P(У/E) = 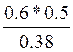=0,78

P(X/G) = 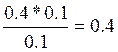                                P(У/G) = 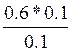=0,6

P(X/Z) = 0                                                      P(У/Z) = 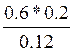=1

5. Составим матрицу обратных условных вероятностей.

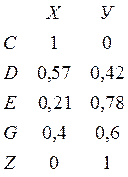
6. Энтропия входа.

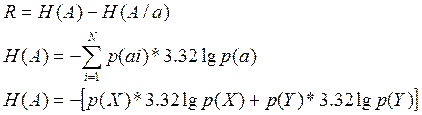
H(A) =0.88;

7. Условная энтропия.

=0

H(X/D) = 0.76

H(X/E) = 0,99

H(X/G) = 0,99

H(X/Z) = 0

Общее значение:

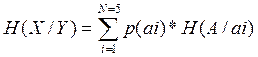
H(X/a) = 0.4923

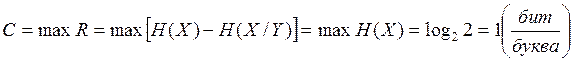
C = 0.88-0.4923=0.3877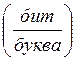

Выполним разбиение на основе графа условных обратных вероятностей:

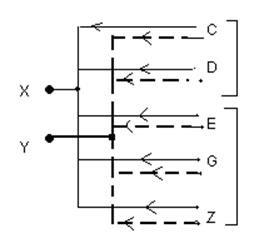
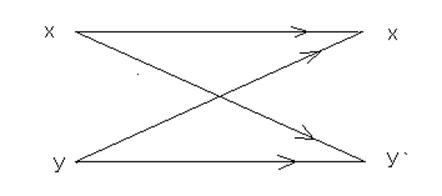
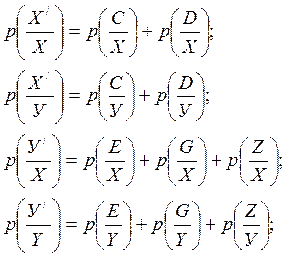
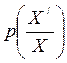 = 0,5+0,3+0,1=0,9

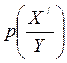 = 0+0,2+0,2=0,4

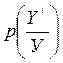 = 0,3+0,3=0,6

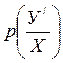  =0+0,1=0,1

p(X ^/ ) = p(C)+p(D) + = 0,35 +0,27 =0,68

p(У ^/ ) = p(E) + p(G) + p(Z)  =  0,13 +0,16+0,09 = 0,32

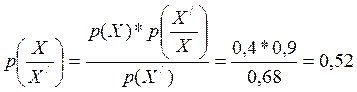
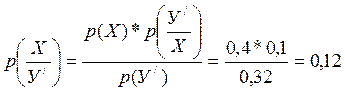
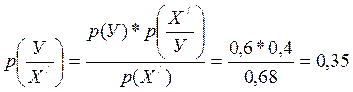
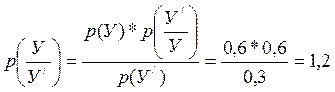
H(A/X ^/) = 0.63

H(A/X ^/) = 0.95

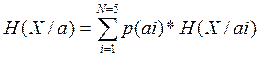
H(X/a) = 0.71

R = 0.88 – 0.71 = 0.17

Вывод:

В ходе выполнения работы мы изучили свойства дискретного канала и его параметры. По исходным данным можно сделать выводы, что данный канал является недвоичным, несимметричным по выходу и источник – с неравной вероятностью и взаимонезависимостью букв.

Получив и рассчитав новый канал передачи сообщения, мы не смогли достигнуть лучшего результата передачи данных по сравнению с расчётом предыдущего канала. Следовательно, можно сказать, что данный способ - оптимального алгоритма работы решающей схемы - не может быть использован с целью получения лучших характеристик передачи сообщений в каналах связи.