





ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
«Исследование дискретного источника информации»
Выполнил студент группы АСВ-208:
Пименов М.Ю.
Проверила: Тулугурова Е.А.
Санкт – Петербург
2004 г.
Задание
BAC BAB BAB ABA BBB BAC AB
ACB ABB BBB BBA BAB ABA BB
BBB BAB ACC BAB BBB BBB AB
ACB ABA CBA BBA BBB ABA BB
1. Определение статистических характеристик источника информации по заданному его сообщению.
1.1 Определение длины сообщения n и алфавита источника.
Длина сообщения n=100 букв.
Алфавит: N=3; A=(A, B, C)
1.2 Определение вероятности появления букв в сообщении.
Данная вероятность определяется по следующей формуле:
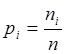
Вычисленные вероятности представлены в таблице 1.
Таблица 1.
|
|
|
|
|
A |
33 |
0,33 |
|
B |
59 |
0,59 |
|
C |
8 |
0,08 |
1.3 Определение вероятностей двухбуквенных сочетаний.
Количество всех
возможных сочетаний из N букв алфавита равно ![]() , а число
всех двухбуквенных сочетаний в сообщении равно
, а число
всех двухбуквенных сочетаний в сообщении равно
![]() Данная вероятность определяется по следующей формуле:
Данная вероятность определяется по следующей формуле:
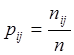
Вычисленные вероятности представлены в таблице 2.
Таблица 2.
|
|
|
|
|
|
AA |
0 |
0 |
0,1 |
|
AB |
25 |
0,25 |
0,19 |
|
AC |
7 |
0,07 |
0,026 |
|
BA |
31 |
0,31 |
0,19 |
|
BB |
28 |
0,28 |
0,35 |
|
BC |
0 |
0 |
0,047 |
|
CA |
2 |
0,02 |
0,026 |
|
CB |
5 |
0,05 |
0,047 |
|
CC |
1 |
0,01 |
0,0064 |
1.4
Определение вероятностей букв, входящих в каждое сочетание ![]() .
.
Данные вероятности представлены в таблице 2, и определяются перемножением соответствующих вероятностей появления букв в сообщении.
Из таблицы 2 видно, что вероятности ![]() и
и ![]() не равны, следовательно, источник информации является марковским.
не равны, следовательно, источник информации является марковским.
1.5 Определение условных вероятностей.
Условные вероятности определяются по следующей формуле:
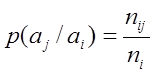
Вычисленные вероятности представлены в таблице 3.
Таблица 3.
|
Последующие буквы |
||||
|
A |
B |
C |
||
|
Предыдущие буквы |
A |
0 |
0,758 |
0,214 |
|
B |
0,525 |
0,475 |
0 |
|
|
C |
0,25 |
0,625 |
0,125 |
|
Граф функционирования марковского источника.
2. Определение информационных характеристик источника и оценка влияния на них неравновероятности и взаимозависимости букв.
2.1 Вычисления энтропии источника:
· В предположении равновероятности и взаимонезависимости букв
![]()
· В предположении неравновероятности и взаимонезависимости букв
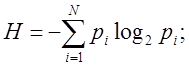
· В предположении неравновероятности и взаимозависимости букв (марковский)
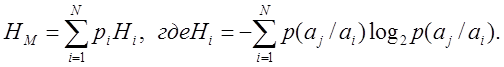
Результаты вычислений представлены в таблице 4.
Таблица 4.
|
Модель источника |
|||
|
Марковская |
С независимыми буквами |
С равновероятными и независимыми буквами |
|
H, бит/букву |
0,95 |
1,268 |
1,585 |
|
E, % |
40 |
20 |
0 |
|
D |
0,6 |
0,8 |
1 |
2.2 Вычисление относительной избыточности E и информативности сообщения D.
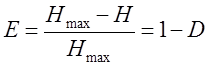
Результаты вычислений представлены в таблице 4.
2.3
Определение количества
информации J и минимального количества двоичных символов
необходимых, для кодирования сообщения ![]() .
.
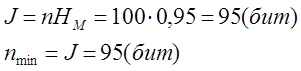
2.4 Определение числа двоичных букв, необходимого для кодирования сообщения равномерным двоичным кодом.
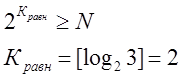
3. Статистическое кодирование сообщений источника
3.1 Цель и принципы статистического кодирования.
Цель статистического кодирования – уменьшение избыточности, вызванной неравновероятностью появления букв. Принцип кодирования:
буквы, которые передаются часто кодируются коротким комбинациями, а буквы , которые передаются редко кодируются длинными комбинациями.
3.2 Построение статистического кода для побуквенного кодирования.
Воспользуемся кодом Фэно. Результаты кодирования представлены в таблице 5.
Таблица 5.
|
|
|
1 |
2 |
Кодовая комбинация |
Число символов |
|
B |
0,59 |
1 |
1 |
1 |
|
|
A |
0,33 |
0 |
1 |
01 |
2 |
|
C |
0,08 |
0 |
0 |
00 |
2 |
Вычислим количество букв статистического кода, необходимого для кодирования стобуквенного сообщения источника:
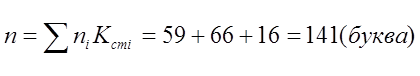
3.3 Статистическое кодирование марковских источников по двухбуквенным сочетаниям.
Воспользуемся кодом Фэно. Результаты кодирования представлены в таблице 6.
Таблица 6.
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
Кодовая комбинация |
Число символов |
BA |
0,31 |
1 |
1 |
1 |
|||||
|
BB |
0,28 |
0 |
1 |
01 |
2 |
||||
|
AB |
0,25 |
0 |
0 |
1 |
001 |
3 |
|||
|
AC |
0,07 |
0 |
0 |
0 |
1 |
0001 |
4 |
||
|
CB |
0,05 |
0 |
0 |
0 |
0 |
1 |
00001 |
5 |
|
|
CA |
0,02 |
0 |
0 |
0 |
0 |
0 |
1 |
000001 |
6 |
|
CC |
0,01 |
0 |
0 |
0 |
0 |
0 |
0 |
000000 |
6 |
Вычислим количество букв статистического кода, необходимого для кодирования двухбуквенных сочетаний стобуквенного сообщения источника:
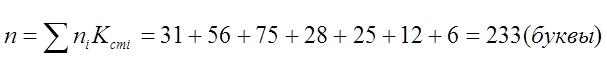
3.4 Оценка влияния взаимозависимости букв на эффективность статистического
кодирования.
Вычислим остаточную избыточность Eост по формуле:
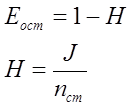
· Для по буквенного кодирования
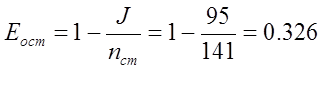
· Для кодирования по двухбуквенным сочетаниям
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.