Определение параметров сигналов и устройств системы передачи информации (количество железнодорожных станций на участке - 15, количество стрелок на каждой станции - 15)

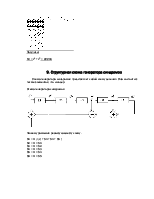
Видно ,что все три условия выполняются, значит производящий многочлен g(x) взят правильно.

Производящий многочлен.

g(x) = x⁵ + x² + x+ 1

5.  Кодовую комбинацию теоретически.

1. Кодируем l(x) – для последней станции, для последней стрелки

Дано:

Nст = 15 - число станций

Nоб = 15 – число стрелок

2^k1 = Nст     k1 = 4

Nст = 15 – 1111

2^k2 = Nоб    k2 = 4

Nоб = 15  - 1111

k3 = 1 – состояние стрелок

l(x) = x⁸+x⁷+ x⁶+ x⁵+ x⁴+ x³+ x²+ x¹+ 1  -   111111111

2. Многочлен l(x)∙х^n-k делится на производящий многочлен g(x)

l(x) × x^n-k = (x⁸+x⁷+ x⁶+ x⁵+ x⁴+ x³+ x²+ x¹+ 1) × x⁵ =  x¹³+x¹²+ x¹¹+ x¹⁰+ x⁹+ x⁸+ x⁷+ x⁶+ x⁵

3.  Находим остаток от деления R(x)

l(x) × x^n-k                        R(x)

------------- =  l(x)” + ----------g(x)                           g(x)

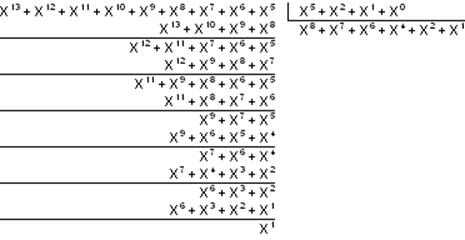
R(x) = x¹  -   000010

4. Находим кодовую комбинацию теоретически  V(x)

V(x) =  l(x) × x^n-k  + R(x) = x¹³+x¹²+ x¹¹+ x¹⁰+ x⁹+ x⁸+ x⁷+ x⁶+ x⁵+ x¹

V(x) = 11111111100010

6.  Структурную схему кодера.

g(x) = x⁵ + x² + x  + 1

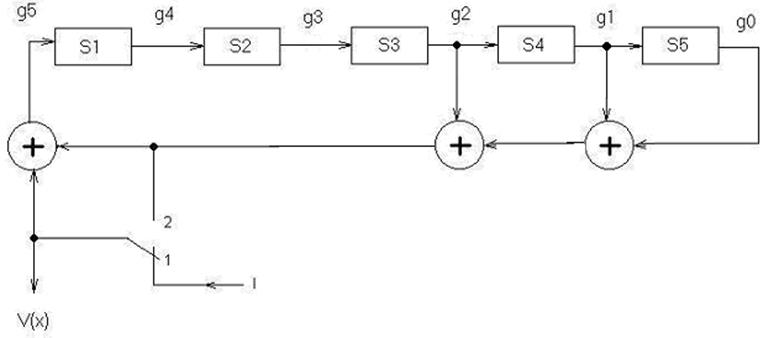
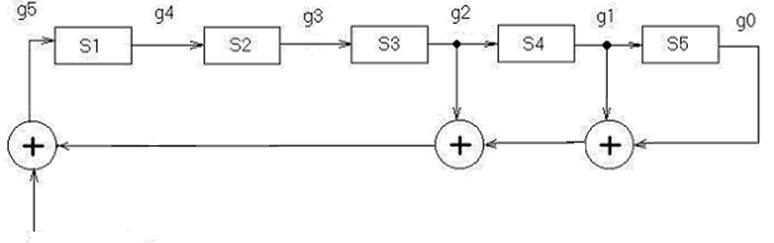
Схема кодера, реализующего алгоритм кодирования, строится по производящему многочлену g(x) и представляет собой схему деления на g(x).Схема состоит из n-k элементов регистра сдвига D-триггеров (S1-S5) и сумматоров по модулю 2

Количество элементов задержки равно старшей степени в полиноме g(x) - 5

Количество сумматоров равно количеству знаков «+» в полиноме g(x) – 3

Строим структурную схему кодера.

7.  Таблицу состояний элементов регистров сдвига

кодера систематического (n.k) – кода.

Для описания работы схемы кодера составляются уравнения функционирования элементов регистра сдвига. При этом вводится понятие задержки на один такт; Запаздывание на один такт обозначим символом D. Тогда функционирование схемы будут определять следующие уравнения:

Составляем систему уравнений для данного кодера.

Для положения ключа “1”

S1 = D ( l(x) +  S5 + S4 + S3 )

S2 = D × S1

S3 = D × S2

S4 = D × S3

S5 = D × S4

S6 = D × S5

Для положения ключа “2”

V(x) = S5 + S4 + S3     S1 = 0     

l(x) = x⁸+x⁷+ x⁶+ x⁵+ x⁴+ x³+ x²+ x¹+ 1

V(x) = x¹³+x¹²+ x¹¹+ x¹⁰+ x⁹+ x⁸+ x⁷+ x⁶+ x⁵+ x¹

Таблица состояний элементов сдвига кодера

На выходе кодера получили кодовую комбинацию V=11111111100010, которая соответствует теоретическому полиному V(x)= x¹³+x¹²+ x¹¹+ x¹⁰+ x⁹+ x⁸+ x⁷+ x⁶+ x⁵+ x¹

8.  Теоретический и аппаратный синдромы: одиночной и  двойной смежной ошибки.

Общий принцип обнаружения и исправления ошибок при использовании циклического кода заключается в том, что при ошибках деление на приёмной станции идёт с остатком, и если разным ошибкам соответствуют разные остатки, последние используются как синдромы. Синдром ошибки может быть теоретическим, а может быть аппаратным. Обычно они не совпадают.  Определим теоретические синдромы для одиночной, двойной и тройной смежных ошибок. При этом необходимо учесть, что количество импульсов в синдроме должно быть n-k.

Ищем теоретический синдром одиночной ошибки.

е(х)

---------- синдром находится, как остаток от деления

g(х)

е(х) = х^n-1 = х^14-1 = х¹³

g(x) = x⁵ + x² + x  + 1

Так как при таком делении теоретический синдром, как правило, отличается от аппаратного ищем сразу модифицированный синдром

е(х)мод = е(х) * х^n-k = х¹³ * х⁵ = х¹⁸

Считаем теоретический синдром для одиночной ошибки Е1

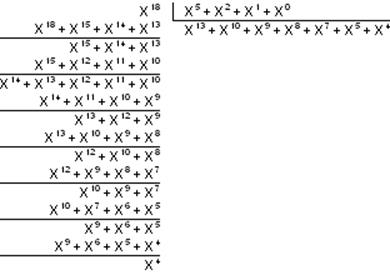
Получили:

Е1 = x⁴ = 00001

Ищем теоретический синдром двойной смежной ошибки.

е(х)

---------- синдром находится, как остаток от деления

g(х)

е(х) = х^n-1 + х^n-2 = х^14-1 + х^14-2 = х¹³ + х¹²

g(x) = x⁵ + x² + x  + 1

Так как при таком делении теоретический синдром, как правило, отличается от аппаратного ищем сразу модифицированный синдром

е(х)мод = е(х) * х^n-k = ( х¹³ + х¹² ) * х⁵ = х¹⁸ + х¹⁷

Считаем теоретический синдром для двойной смежной ошибки Е2

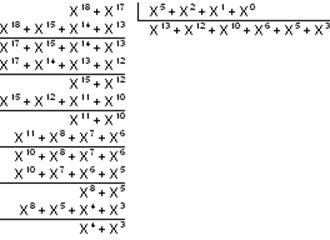
Получили:

Е2 = x⁴ + x³ = 00011

9.  Структурная схема генератора синдромов

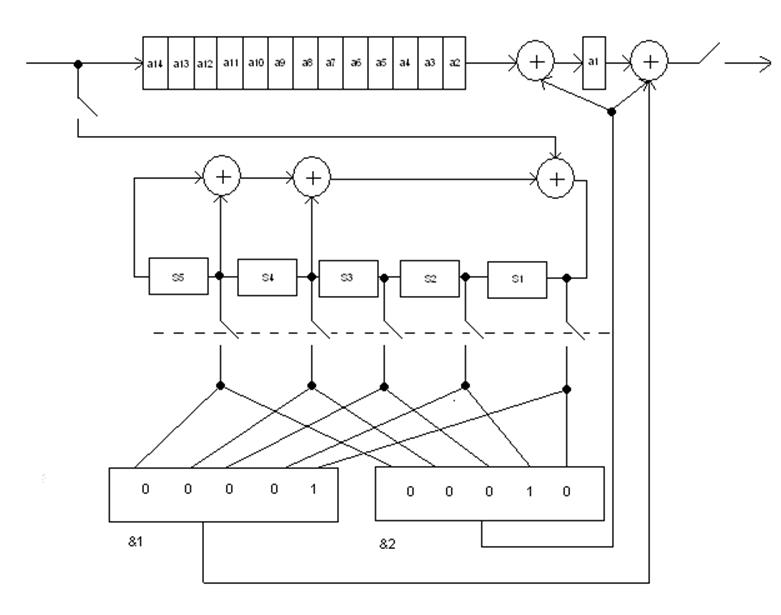
Схема генератора синдромов представляет собой схему деления. Она состоит из тех же элементов, что и кодер.

Схема генератора синдромов.

Пишем уравнения реализующие эту схему.

S1 = D ( l(x) + S4 + S4 + S5 )

S2 = D × S1

S3 = D × S2

S4 = D × S3

S5 = D × S4

S6 = D × S5

Ищем аппаратный синдром одиночной ошибки.

Е1 = 00001

Ищем аппаратный синдром двойной смежной ошибки.

Е2 = 00011

Теоретические синдромы, из пункта 8, полностью сходятся с оппаратными синдромами.

Данный генератор синдромов подходит для нас.

10.  Таблицу состояний элементов регистра сдвига генератора синдромов декодера на примере ошибочно принятой кодовой комбинации.

Теперь подадим на вход комбинацию V(x), допустив ошибку во втором такте.

V(x)= x¹³+x¹²+ x¹¹+ x¹⁰+ x⁹+ x⁸+ x⁷+ x⁶+ x⁵+ x¹

Промоделируем работу схемы.

Промоделировав схему с одиночной ошибкой во втором такте мы получили синдром ошибки в 16 такте.   Схема работает, ошибки обнаруживаются.

Теперь подадим на вход комбинацию V(x), допустив ошибку во втором и третем такте.

V(x)= x¹³+x¹²+ x¹¹+ x¹⁰+ x⁹+ x⁸+ x⁷+ x⁶+ x⁵+ x¹

Промоделировав схему с одиночной ошибкой во втором такте мы получили синдром ошибки в 16 такте.   Схема работает, ошибки обнаруживаются. 

                      11 Структурная схема декодера.

12.  Амплитуда импульсов на входе канала ТУ.

Длительность импульсов.

Uвх = А – амплитуда импульсов на входе а – затухание канала ТУ

х – аргумент функции Крампа

D – действующее значение напряжения помехи на выходе канала ТУ

х можно найти по таблице, зная значение функции Крампа:

Ф(х) = 1 – 2·Ре , где  Ф(х) – функция ошибок

Ре – вероятность ошибки на выходе канала ТУ

Ф(х) = 1 – 2·3,9·10 ^-3 = 0.9922

По таблице находим х = 3

U_п

Х= ----------- →   U_п=х√2D,

√2D

D = 13 ∙10^-4 В

U_п= х√2∙D = 3√2* 13 ∙10^-4 = 0.153 В

U_вых=2U_п

U_вых= 2* 0.153 = 0.306 В

U_вх=10 ^а/20∙U_вых= 0.306 * 10 ^15/20 = 1.72 В

U_вх=А= 1.72 В

Длительность импульсов вычисляется по формуле:

Тпер

Т_и =  ----------               

N     

N =  Ncc + n* Nст = 15 + 14 * 15 = 225

Т_и=200/225= 0,89 сек.

13.  Передаточная функция фильтра, согласованного с одиночными импульсами

1

Согласно исходным данным, импульс в канале ДУ  1+ 0- . передаточная функция фильтра находится по следующим формулам:

1.Найти спектр сигнала, с которым фильтр согласован

                                     _{T/2                     T}              -A         _T/2               A            _T              -A                 A       

1.  U(jw)=∫ Ae^-jwt dt +∫ -Ae^-jwt =   jw  e^-jwt              +    jw  e^-jwt            =    jw   e^-jwT/2 +   jw   +   

                                      ^{0                         T/2                               0                                     T/2}

A   e^-jwT       A   e^-jwT/2       A         A   e^-jwT     2A   e^-jwT/2

+  jw         -     jw            =    jw   +   jw          -   jw

2.Записать комплексно сопряженный спектр

_•

         U(jw)= -A        A   e^jwT      2A   e^jwT/2

jw  -    jw         +   jw

3.Записать передаточную функцию

_•

H(jw)=U(jw)e^-jwT= -A  e^-jwT      A  e^jwT e^-jwT        2A  e^jwT/2 e^-jwT      - A e^-jwT       A

                                        jw         -   jw                  +    jw                   =    jw        -   jw   +

2A  e^-jwT/2     -A  e^-jwT/2 e^-jwT            A        A  e^-jwT/2       A   e^-jwT/2      A                     A   e^-jwT/2

+   jw          =     jw                   -     jw   +  jw       +     jw           =    jw   (e^-jwT/2-1) -  jw           *

A

*(e^-jwT/2-1)=   jw (e^-jwT/2-1)(1-e^-jwT/2)

Подставляем А=1,72

1,72

         Н(jw)=    jw    (e^-jwT/2-1)(1-e^-jwT/2)

14.  Структурная схема согласованного фильтра

     Схему согласованного фильтра строят по передаточной функции H(jw). Умножение на 1/jw соответствует интегрированию; умножение на e^-jwT/2 соответствует задержке сигнала на Т/2.

∫dt             ∫dt    интегратор с коэффициентом передачи 1/jw

                        Т/2    линия задержки на время Т/2

                                   вычитающее  устройство

Схема согласованного фильтра для биимпульса, выглядит так:

Схема согласованного фильтра для биимпульса с задержкой, выглядит так:

Обе схемы включены параллельно. Первая схема следит за появлением первого вида сигналов, а вторая за появлением второго вида сигналов.

На выходе согласованного фильтра получается сигнал, который является автокорреляционной функцией.

15. Структурная схема фильтра, согласованного с комбинацией синхросигнала.

Комбинацию импульсов синхросигнала необходимо подобрать так, чтобы